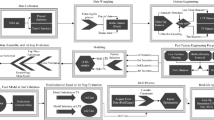
Abstract
The study focuses on applying machine learning methodologies to football player data for predicting player market values in the dynamic football market. Player datasets are rich, encompassing performance metrics, physiological attributes, and contextual variables. Machine learning models, including both traditional and advanced methods, effectively extract insights from complex data to estimate player market values. Addressing challenges like overfitting and computational complexity involves applying regularization, feature engineering, and interpretability tools to manage high-dimensional data and improve predictive accuracy. In this study sensitivity of selected models (Support Vector Regression (SVR), Random Forest Regression (RFR), Extreme Gradient Boosting (XGB), and Categorical Boosting (CAT)) models to extracted data from FIFA 19 and Real-world Statistical Datasets evaluated by Shapley Additive Explanations (SHAP) and the 20 most relevant features selected in the ranking of SHAP for each regression model. Then, models optimized with two meta-heuristic algorithms demonstrated their performance in predicting the market values of players. Dempster-Shafer Theory (DST) was utilized to develop an ensemble of models to overcome overfitting problems, and Fourier amplitude sensitivity testing (FAST) gave insight for future data extractions. The analysis of market values for players revealed significant model performance variations. XGSC hybrid model demonstrated exceptional precision with a minimal error of 1.7 million dollars (10% of average measured value), followed by RSCX_SC with misestimations of 2 million dollars (13.3% of average measured value). Extracted results suggested that models, especially ensemble form, offer reliable accuracy for club managers and stakeholders, aiding in strategic player selection based on previous performance. This approach proves particularly beneficial for optimizing player salaries, especially when considering a prominent team with market values above average.
















Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
Not applicable.
Abbreviations
- RFR:
-
Random Forest Regression
- RF:
-
Random Forest
- \(\:{R}_{n}\) :
-
Training dataset with \(n\) data points
- \(X\) :
-
Input vector
- \(\:m\) :
-
Number of features
- \(Y\) :
-
Single-valued output
- \(\widehat{H}\) :
-
Predictive function
- \(\:{\varTheta\:}_{K}\) :
-
Randomly generated vectors
- \(\:\widehat{Y}\) :
-
Final predicted value
- \({n}_{tree}\) :
-
Number of trees
- \(\:{m}_{try}\) :
-
The number of randomly selected attributes for each tree division
- SVR:
-
Support Vector Regression
- \(\epsilon\) :
-
Noise parameter
- \(\:{y}_{i}\) :
-
Dependent variable
- \(\langle w,{x}_{i}\rangle\) :
-
The dot product of the weight Vector and feature vector
- \(\:b\) :
-
Error term added in
- CAT:
-
Categorical Boosting
- XGB:
-
Extreme Gradient Boosting
- DS:
-
Dataset
- \(\:k\) :
-
Variable that specifies the number of trees
- \(\:{f}_{k}\) :
-
\(\:k-th\) tree
- \(\:{\Omega\:}\) :
-
The parameter presenting the complexity of the model
- \(\:w\) :
-
The weight of each leaf
- \(\:T\) :
-
The total number of leaves
- t :
-
Iteration number
- HGSO:
-
Hunger Games Search Optimization
- \(\:\overrightarrow{X\left(t\right)}\) :
-
Individual positions
- \(\:{\overrightarrow{X}}_{b}\) :
-
The best individual's position
- \(\:{\overrightarrow{W}}_{1}\) :
-
Hunger weight
- \(\:{\overrightarrow{W}}_{2}\) :
-
Hunger weight
- \(\:{r}_{1}\) :
-
Random number
- \(\:{r}_{2}\) :
-
Random number
- l :
-
Sensitivity control variable
- E :
-
Variation control parameter
- \(\:F\left(i\right)\) :
-
Cost function value for each population
- BF :
-
Best cost function value achieved in the current iteration
- Sech :
-
Hyperbolic function
- \(\:{Max}_{iter}\) :
-
Upper limit of iterations
- N :
-
Population size
- \(\:{r}_{3}\) :
-
Random number
- \(\:{r}_{4}\) :
-
Random number
- \(\:{r}_{5}\) :
-
Random number
- \(\:AllFitness\left(i\right).\) :
-
Cost function value of each population in the current iteration
- WF :
-
Worst fitness
- BF :
-
Best fitness
- \(\:{r}_{6}\) :
-
Random number
- SCSO:
-
Sand Cat Swarm Optimization
- \(\:\overrightarrow{X}\) :
-
Positional vector of the search agent
- \(\:{\overrightarrow{X}}_{b}\left(t\right)\) :
-
The location of the leading contender during iteration t
- \(\:{\overrightarrow{X}}_{c}\left(t\right)\) :
-
The most recent location of the hunting agent at repetition t
- \(\:{\overrightarrow{r}}_{G}\) :
-
Overall sensitivity span
- \(\:ite{r}_{c}\) :
-
The current iteration
- \(\:\theta\:\) :
-
Arbitrary angle between 0 and 360 degrees
- \(\:{\overrightarrow{X}}_{md}\) :
-
A position formed by combining the optimal and current positions
- SHAP:
-
Shapley Additive Explanations
- z :
-
Binary vector
- \(\varphi_i\) :
-
Feature attribution value
- F :
-
The non-zero set of inputs in z
- S :
-
The subset of F with the ith feature excluded
- R2 :
-
Coefficient of determination
- RMSE:
-
Root Mean Square Error
- MAE:
-
Mean Absolute Error
- NMSE:
-
Normalized Mean Square Error
- PI:
-
Prediction Interval
- \(\:{P}_{i}\) :
-
Predicted market values
- \(\:\stackrel{-}{P}\) :
-
Average of all predicted values
- \(\:{M}_{i}\) :
-
Real market values
- \(\:\stackrel{-}{M}\) :
-
An average of all real values
- \(\:{k}^{2}\) :
-
Standardized error value
- \(\:{\text{t}}_{({\upalpha\:}/2,\:\:\:\text{N}-2)}\) :
-
t-value for the desired level of confidence (\(\:\alpha\:\)) and the degrees of freedom (\(\:N-2\))
References
Camp W, Deland LF (1896) Football. Houghton, Mifflin
Garcia del Barrio P, Pujol F (2016) Economic evaluation of football players through media value, vol 9(3). University of London, pp 1–32
Majewski S (2016) Identification of factors determining market value of the most valuable football players. Cent Eur Manage J 24(3):91–104
Metelski A (2021) Factors affecting the value of football players in the transfer market. J Phys Educ Sport 21:1150–1155
Felipe JL, Fernandez-Luna A, Burillo P, de la Riva LE, Sanchez-Sanchez J, Garcia-Unanue J (2020) Money talks: team variables and player positions that most influence the market value of professional male footballers in Europe. Sustainability 12(9):3709
Serna Rodríguez M, Ramírez Hassan A, Coad A (2019) Uncovering value drivers of high performance soccer players. J Sports Econ 20(6):819–849
Matschke MJ, Brösel G (2021) Business valuation: functions, methods, principles. Einbandgestaltung, Atelier Reichert, Stuttgart
Oprean V-B, Oprisor T (2014) Accounting for soccer players: capitalization paradigm vs. expenditure. Procedia Econ Finance 15:1647–1654
Pavlović V, Milačić S, Ljumović I (2014) Controversies about the accounting treatment of transfer fee in the football industry. Manag: J Sustain Bus Manage Solut Emerg Econ 19(70):17–24
Brocard J-F, Cavagnac M (2012) Who should pay the sports agent’s commission? An economic analysis of setting the legal rules in the regulation of matchmakers. https://tse-fr.eu/pub/27145
Ackermann P, Follert F (2018) Einige bewertungstheoretische Anmerkungen zur Marktwertanalyse der Plattform transfermarkt. de, Diskussionspapiere des Europäischen Instituts für Sozioökonomie eV
Rubio Martin G, Manuel García CM, Rodríguez-López Á, Gonzalez Sanchez FJ (2022) Measuring football clubs’ human capital: analytical and dynamic models based on footballers’ life cycles. J Intellect Capital 23(5):1107–1137
Richau L, Follert F, Frenger M, Emrich E (2010) Performance indicators in football: the im-portance of actual performance for the market value of football players. Sciamus–Sport Und Manage 10:41–67
Behravan I, Razavi SM (2021) A novel machine learning method for estimating football players’ value in the transfer market. Soft Comput 25(3):2499–2511
Oliver JL, Ayala F, Croix MBADS, Lloyd RS, Myer GD, Read PJ (2020) Using machine learning to improve our understanding of injury risk and prediction in elite male youth football players. J Sci Med Sport 23(11):1044–1048
Ezzeddine M (2020) Pricing football transfers: determinants, inflation, sustainability, and market impact: finance, economics, and machine learning approaches. Université Panthéon-Sorbonne - Paris I
Jamil M, Phatak A, Mehta S, Beato M, Memmert D, Connor M (2021) Using multiple machine learning algorithms to classify elite and sub-elite goalkeepers in professional men’s football. Sci Rep 11(1):22703
Inan T, Cavas L (2021) Estimation of market values of football players through artificial neural network: a model study from the Turkish super league. Appl Artif Intell 35(13):1022–1042
Krishna G, Chandran AS (2021) Predictive analysis of football player market value using machine learning
Li C, Kampakis S, Treleaven P (2022) Machine learning modeling to evaluate the value of football players. arXiv preprint arXiv:2207.11361
McHale IG, Holmes B (2023) Estimating transfer fees of professional footballers using advanced performance metrics and machine learning. Eur J Oper Res 306(1):389–399. https://doi.org/10.1016/j.ejor.2022.06.033
Wang Y, Tarakci H, Prybutok V (2023) Model comparison of regression, neural networks, and XGBoost as applied to the English Premier League transfer market. Int J Sport Manage Mark 23(6):543–559
Lee H, Tama BA, Cha M (2022) Prediction of Football Player Value using Bayesian Ensemble Approach. arXiv preprint arXiv:2206.13246
Al-Asadi MA, Tasdemır S (2022) Predict the value of football players using FIFA video game data and machine learning techniques. IEEE Access 10:22631–22645
Hucaljuk J, Rakipović A (2011) Predicting football scores using machine learning techniques. In: 2011 Proceedings of the 34th International Convention MIPRO, IEEE, pp 1623–1627
Joseph A, Fenton NE, Neil M (2006) Predicting football results using bayesian nets and other machine learning techniques. Knowl Based Syst 19(7):544–553
Van Eetvelde H, Mendonça LD, Ley C, Seil R, Tischer T (2021) Machine learning methods in sport injury prediction and prevention: a systematic review. J Exp Orthop 8:1–15
Breiman L, Friedman J, Olshen R, Stone C (1984) Classification and regression trees. CRC Press, Boca Raton
Ikeagwuani CC (2021) Estimation of modified expansive soil CBR with multivariate adaptive regression splines, random forest and gradient boosting machine. Innovative Infrastructure Solutions 6(4):199
Vu DQ, Nguyen DD, Bui Q-AT, Trong DK, Prakash I, Pham BT (2021) Estimation of California bearing ratio of soils using random forest based machine learning. J Sci Transp Technol 1(1):45–58
Breiman L (2001) Random forests. Mach Learn 45:5–32
Rodriguez-Galiano V, Sanchez-Castillo M, Chica-Olmo M, Chica-Rivas M (2015) Machine learning predictive models for mineral prospectivity: an evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol Rev 71:804–818
Liaw A, Wiener M (2002) Classification and regression by randomForest. R news 2(3):18–22
Peters J et al (2007) Random Forests as a tool for ecohydrological distribution modelling. Ecol Modell 207:304–318. https://doi.org/10.1016/j.ecolmodel.2007.05.011
Wu Y, He X (2024) Using the automated random forest approach for obtaining the compressive strength prediction of RCA. Multiscale Multidisciplinary Model Experiments Des 7(2):855–867
Vapnik VN (1995) The nature of statistical learning. Theory, Springer
Laros GGPK (2022) Predicting transfer value of professional football players based on player skills and characteristics using multiple linear regression, support vector regression, and random forest regression, Tilburg University
Smola AJ, Schölkopf B (2004) A tutorial on support vector regression. Stat Comput 14(3):199–222
Prokhorenkova L, Gusev G, Vorobev A, Dorogush AV, Gulin A (2018) CatBoost: unbiased boosting with categorical features. Adv Neural Inf Process Syst, 31
Razali MN, Mustapha A, Mostafa SA, Gunasekaran SS (2022) Football matches outcomes prediction based on gradient boosting algorithms and football rating system. Hum Factors Softw Syst Eng 61:57
Chen T, Guestrin C (2016) Xgboost: A scalable tree boosting system. In: Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, pp 785–794
Yang Y, Chen H, Heidari AA, Gandomi AH (2021) Hunger games search: visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst Appl 177:114864
Seyyedabbasi A, Kiani F (2023) Sand cat swarm optimization: a nature-inspired algorithm to solve global optimization problems. Eng Comput 39(4):2627–2651
Yue L, Liu X, Chang S (2024) Appraising the building cooling load via Hybrid Framework of Machine Learning techniques. Int J Adv Comput Sci Appl 15:6
Li Y, Wang G (2022) Sand cat swarm optimization based on stochastic variation with elite collaboration. IEEE Access 10:89989–90003
Wicker P, Prinz J, Weimar D, Deutscher C, Upmann T (2013) No Pain, no Gain? Effort and Productivity in Professional Soccer. Int J Sport Finance 8:2
Idson TL, Kahane LH (2000) Team effects on compensation: an application to salary determination in the National Hockey League. Econ Inq 38(2):345–357
Kahn LM (2000) The sports business as a labor market laboratory. J Economic Perspect 14(3):75–94
Herm S, Callsen-Bracker H-M, Kreis H (2014) When the crowd evaluates soccer players’ market values: accuracy and evaluation attributes of an online community. Sport Manage Rev 17(4):484–492
Müller O, Simons A, Weinmann M (2017) Beyond crowd judgments: Data-driven estimation of market value in association football. Eur J Oper Res 263(2):611–624
Lucifora C, Simmons R (2003) Superstar effects in sport: evidence from Italian soccer. J Sports Econom 4(1):35–55
Bryson A, Frick B, Simmons R (2009) The returns to scarce talent: footedness and player remuneration in European football. J Sports Econ 14(6):606–628
Franck E, Nüesch S (2012) Talent and/or popularity: what does it take to be a superstar? Econ Inq 50(1):202–216
FootballPlayersDataset. [Online] Available: https://www.openml.org/search?type=data&status=active&id=43604. Accessed 24 Mar 2022
Lundberg SM, Lee S-I (2017) A unified approach to interpreting model predictions. Adv Neural Inf Process Syst 30:4765-74
Lundberg SM, Erion GG, Lee S-I (2018) Consistent individualized feature attribution for tree ensembles, arXiv preprint arXiv:1802.03888
Lundberg SM, Lee S-I (2017) Consistent feature attribution for tree ensembles. arXiv preprint arXiv:1706.06060
Reusser DE, Buytaert W, Zehe E (2011) Temporal dynamics of model parameter sensitivity for computationally expensive models with the Fourier amplitude sensitivity test. Water Resour Res 47:7
Cukier RI, Schaibly JH, Shuler KE (1975) Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. III. Analysis of the approximations. J Chem Phys 63(3):1140–1149
Funding
None.
Author information
Authors and Affiliations
Contributions
Study conception and design, data collection, simulation and analysis, The first draft of the manuscript: Qijie Shen.
Corresponding author
Ethics declarations
Human participants and/or animals
Not applicable.
Ethical approval
Not applicable.
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Shen, Q. Predicting the value of football players: machine learning techniques and sensitivity analysis based on FIFA and real-world statistical datasets. Appl Intell 55, 265 (2025). https://doi.org/10.1007/s10489-024-06189-0
Accepted:
Published:
DOI: https://doi.org/10.1007/s10489-024-06189-0