Skip to main content

Advertisement

Springer Nature Link
Log in

Design and analysis of a variable-parameter noise-tolerant ZNN for solving time-variant nonlinear equations and applications

  • Published:
Applied Intelligence Aims and scope Submit manuscript

Abstract

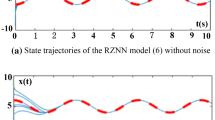
Solvers considering time-varying parameters are more suitable for addressing a variety of time-varying problems, whereas traditional fixed-parameter neural networks are somewhat insufficient for efficiently and quickly solving these problems. Many existing zeroing neural networks ensure rapid convergence using the infinite-valued AFs. For solving time-varying nonlinear equations, this paper proposes a finitely-activated variable parameter noise tolerant zeroing neural network (VPNTZNN), applied to trajectory tracking of redundant robotic arms. The designed variable parameters are error-dependent, enabling adaptive adjustment to optimal values as errors fluctuate, thereby ensuring faster convergence of the proposed VPNTZNN. And the constructed variable parameters and activation functions (AFs) do not escalate infinitely over time. Affected by the above variable parameters, the proposed finitely-activated VPNTZNN achieves rapid finite-time convergence with strong noise suppression. Simulation results validate the effectiveness of our method in solving time-variant nonlinear equations and in trajectory tracking of redundant manipulators. Moreover, this approach employs a finite-valued activation function to design a variable-parameter neural network, thereby avoiding the difficulties of practical implementation.

Graphical abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

  1. Khan Y (2021) Novel solitary wave solution of the nonlinear fractal schrdinger equation and its fractal variational principle. Math Probl Eng 17:630–635

    Google Scholar 

  2. Behera R, Gerontitis D, Stanimirovic P, Katsikis V, Shi Y, Cao X (2023) An efficient zeroing neural network for solving time-varying nonlinear equations. Neural Comput Appl 35:17537–17554

    Article  Google Scholar 

  3. Li J, Shi Y, Xuan H (2021) Unified model solving nine types of time-varying problems in the frame of zeroing neural network. IEEE Trans Neural Netw Learn Syst 32:1896–1905

    Article  MathSciNet  Google Scholar 

  4. Xiao L, Xiao S, He Y, Dai J, Wang Y, Li Y (2024) Comprehensive study on zeroing neural network with high-order evolutionary formula, nonlinear functions, and variable parameter for time-changing matrix cholesky decomposition. IEEE Trans Syst Man Cybern Syst 54:3642–3651

    Article  Google Scholar 

  5. Zhang Y, Zhang Y, Chen D, Xiao Z, Yan X (2017) From davidenko method to zhang dynamics for nonlinear equation systems solving. IEEE Trans Syst Man Cybern Syst 47:2817–2830

    Article  Google Scholar 

  6. Jin J, Chen W, Chen C, Chen L, Tang Z, Chen L, Wu L, Zu C (2023) A predefined fixed time convergence ZNN and its applications to time-varying quadratic programming solving and dual-arm manipulator cooperative trajectory tracking. IEEE Trans Ind Inform 19:8691–8702

    Article  Google Scholar 

  7. Luo J, Yang H, Yuan L, Chen H, Wang X (2022) Hyperbolic tangent variant-parameter robust ZNN schemes for solving time-varying control equations and tracking of mobile robot. IEEE Trans Ind Inform 510:218–232

    Google Scholar 

  8. Sun Z, Fei Y, Tang S, Xiao X, Luo J, Liu K (2024) A noise suppression zeroing neural network for trajectory tracking with joint angle constraints of mobile manipulator. Eng Appl Artif Intel 133:108173

    Article  Google Scholar 

  9. Tan Z, Xiao L, Chen S, Lv X (2020) Noise-tolerant and finite-time convergent ZNN models for dynamic matrix moore-penrose inversion. IEEE Trans Ind Inform 16:1591–1601

    Article  Google Scholar 

  10. Li W, Xiao L, Liao B (2020) A finite-time convergent and noise-rejection recurrent neural network and its discretization for dynamic nonlinear equations solving. IEEE Trans Neural Netw Learn Syst 50:3195–3207

  11. Wu W, Zhang Y (2024) Zeroing neural network with coefficient functions and adjustable parameters for solving time-variant sylvester equation. IEEE Trans Neural Netw Learn Syst 35:6757–6766

    Article  MathSciNet  Google Scholar 

  12. Sun M, Li H, Li W (2019) On finite-duration convergent attracting laws. IEEE Trans Syst Man Cybern Syst pp:1-13

  13. Xiao L, Zhang Z, Li S (2019) Solving time-varying system of nonlinear equations by finite time recurrent neural networks with application to motion tracking of robot manipulators. IEEE Trans Syst Man Cybern Syst 49:2210–2220

    Article  Google Scholar 

  14. Hu Z, Xiao L, Li KL, Li KQ, Li JC (2021) Performance analysis of nonlinear activated zeroing neural networks for time-varying matrix pseudoinversion with application. Appl Soft Comput 98:106735

    Article  Google Scholar 

  15. Li W, Ma X, Luo J, Jin L (2021) A strictly predefined-time convergent neural solution to equality- and inequality-constrained time-variant quadratic programming. IEEE Trans Syst Man Cybern Syst 51:4028–4039

    Article  Google Scholar 

  16. Hu Z, Xiao L, Dai J, Xu Y, Zuo Q, Liu C (2021) A unified predefinedtime convergent and robust ZNN model for constrained quadratic programming. IEEE Trans Ind Inform 17:1998–2010

    Article  Google Scholar 

  17. Xiao L, Cao Y, Dai J, Jia L, Tan H (2021) Finite-time and predefined-time convergence design for zeroing neural network: theorem, method, and verification. IEEE Trans Ind Informat 17:4724–4732

    Article  Google Scholar 

  18. Dai J, Jia L, Xiao L (2021) Design and analysis of two prescribed-time and robust ZNN models with application to time-variant stein matrix equation. IEEE Trans Neural Netw Learn Syst 32:1668–1677

    Article  MathSciNet  Google Scholar 

  19. Xiao L, He Y, Liao B (2022) A parameter-changing zeroing neural network for solving linear equations with superior fixed-time convergence. Expert Syst Appl 208:118086

    Article  Google Scholar 

  20. Xiao L, He Y, Dai J, Liu X, Liao B, Tan H (2022) A variable-parameter noise-tolerant zeroing neural network for time-variant matrix inversion with guaranteed robustness. IEEE Trans Neural Netw Learn Syst 33:1535–1545

    Article  MathSciNet  Google Scholar 

  21. Qi Z, Ning Y, Xiao L, Luo J, Li X (2023) Finite-time zeroing neural networks with novel activation function and variable parameter for solving time-varying Lyapunov tensor equation. Appl Math Comput 452:128072

    MathSciNet  Google Scholar 

  22. Jia L, Xiao L, Dai J, Qi Z, Zhang Z, Zhang Y (2021) Design and application of an adaptive fuzzy control strategy to zeroing neural network for solving time-variant QP problem. IEEE Trans Fuzzy Syst 29:1544–1555

    Article  Google Scholar 

  23. Xiao L, Jia L, Wang Y, Dai J, Zhu Q (2022) Performance analysis and applications of finite-time ZNN models with constant/fuzzy parameters for TVQPEI. IEEE Trans Neural Netw Learn Syst 33:6665–6676

    Article  MathSciNet  Google Scholar 

  24. Xiao L, Dai J, Lu R, Li S, Li J, Wang S (2020) Design and comprehensive analysis of a noise-tolerant ZNN model with limited-time convergence for time-dependent nonlinear minimization. IEEE Trans Neural Netw Learn Syst 31:5339–5348

    Article  MathSciNet  Google Scholar 

  25. Zuo Q, Li K, Xiao L (2022) Robust finite-time zeroing neural networks with fixed and varying parameters for solving dynamic generalized lyapunov equation. IEEE Trans Neural Netw Learn Syst 33:7695–7705

    Article  MathSciNet  Google Scholar 

  26. Jin L, Yan J, Du X, Xiao X, Fu D (2020) RNN for solving time-variant generalized sylvester equation with applications to robots and acoustic source localization. IEEE Trans Indus Inform 16:6359–6369

    Article  Google Scholar 

  27. Xiao L, Zhang Z, Li S (2019) Solving time-varying system of nonlinear equations by finite time recurrent neural networks with application to motion tracking of robot manipulators. IEEE Trans Syst Man Cybern Syst 49:2210–2220

    Article  Google Scholar 

  28. Chen D, Li S, Wu Q (2021) A novel supertwisting zeroing neural network with application to mobile robot manipulators. IEEE Trans Neural Netw Learn Syst 32:1776–1787

    Article  MathSciNet  Google Scholar 

  29. Lu H, Jin L, Zhang J, Sun Z, Zhang Z (2021) New joint-drift-free scheme aided with projected ZNN for motion generation of redundant robot manipulators perturbed by disturbances. IEEE Trans Syst Man Cybern Syst 51:5639–5651

    Article  Google Scholar 

  30. Yan X, Liu M, Jin L, Li S, Hu B, Zhang X, Huang Z (2019) New zeroing neural network models for solving nonstationary sylvester equation with verifications on mobile manipulators. IEEE Trans Ind Inform 15:5011–5022

    Article  Google Scholar 

  31. Si Y, Wang D, Chou Y, Fu D (2023) Non-convex activated zeroing neural network model for solving time-varying nonlinear minimization problems with finite-time convergence. Knowl-Based Syst 274:110633

  32. Sun M, Zhang Y, Wu Y, He X (2022) On a finitely activated terminal RNN approach to time-variant problem solving. IEEE Trans Neural Netw Learn Syst 33:7289–7302

    Article  MathSciNet  Google Scholar 

Download references

Funding

This work was supported by the National Natural Science Foundation of China under Grant Nos 62073291 and 62233016.

Author information

Authors and Affiliations

  1. College of Information Engineering, Zhejiang University of Technology, Hangzhou, 310023, China

    Yu Zhang, Liming Wang & Guomin Zhong

Authors
  1. Yu Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Liming Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Guomin Zhong
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Yu Zhang: Conceptualization, Methodology, Formal analysis, Software, Writing-original draft, Writing-review & editing. Liming Wang: Data curation, Formal analysis, Investigation, Writing-original draft. Guomin Zhong: Conceptualization, Methodology, Supervision, Formal analysis, Writing-review & editing.

Corresponding author

Correspondence to Guomin Zhong.

Ethics declarations

Competing Interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Y., Wang, L. & Zhong, G. Design and analysis of a variable-parameter noise-tolerant ZNN for solving time-variant nonlinear equations and applications. Appl Intell 55, 460 (2025). https://doi.org/10.1007/s10489-025-06304-9

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10489-025-06304-9

Keywords