Attention ensemble mixture: a novel offline reinforcement learning algorithm for autonomous vehicles

Abstract

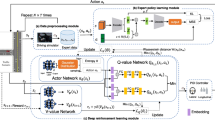
Offline Reinforcement Learning (RL), which optimizes policies from previously collected datasets, is a promising approach for tackling tasks where direct interaction with the environment is infeasible due to high risk or cost of errors, such as autonomous vehicle (AV) applications. However, offline RL faces a critical challenge: extrapolation errors arising from out-of-distribution (OOD) data. In this paper, we propose Attention Ensemble Mixture (AEM), a novel offline RL algorithm that leverages ensemble learning and an attention mechanism. Ensemble learning enhances the confidence of Q-function predictions, while the attention mechanism evaluates the uncertainty of selected actions. By assigning appropriate attention weights to each Q-head, AEM effectively down-weights OOD actions and up-weights in-distribution actions. We further introduce three key improvements to enhance the robustness and generality of AEM: attention-weighted Bellman backups, KL divergence regularization, and delayed attention updates. Extensive comparative experiments demonstrate that AEM outperforms several state-of-the-art ensemble offline RL algorithms, while ablation studies underscore the significance of the proposed enhancements. In AV tasks, AEM exhibits superior performance compared to other methods, excelling in both offline and online evaluations.

Appendices

Appendix A

Theorem 1

Assume that $Q^*(s, a)$ is the optimal Q-function. The Bellman optimality operator is $(\mathcal {T} Q)(s, a):= r + \gamma \mathbb {E}_{P(s'|s, a)}$ $\left[ \mathop {\max }_{a'} Q(s', a') \right] .$ Define $\zeta _{k}(s, a) = \left| Q_{k}(s, a) - Q^{*}(s, a)\right|$ as the total error at the k-th iteration, and define $\delta _{k}(s, a) = \left| Q_{k}(s, a) - \mathcal {T} Q_{k-1}(s, a)\right|$ as the Bellman error at the k-th iteration. Then, we have

$$\begin{aligned} \zeta _{k}(s, a) \le \delta _{k}(s, a) + \gamma \mathop {\max }_{a'} \mathbb {E}_{P(s'|s, a)}\left[ \zeta _{k-1}(s', a')\right] . \end{aligned}$$

(13)

Proof

$$\begin{aligned} \begin{aligned} \zeta _{k}(s, a)&= \left| Q_{k}(s, a) - Q^{*}(s, a)\right| \\&= \left| Q_{k}(s, a) - \mathcal {T} Q_{k-1}(s, a) + \mathcal {T} Q_{k-1}(s, a) - Q^{*}(s, a)\right| \\&\le \left| Q_{k}(s, a) - \mathcal {T} Q_{k-1}(s, a) \right| + \left| \mathcal {T} Q_{k-1}(s, a) - Q^{*}(s, a)\right| \\&= \delta _{k}(s, a) + \left| \mathcal {T} Q_{k-1}(s, a) - \mathcal {T} Q^{*}(s, a)\right|&\! \textcircled {1} \\&= \delta _{k}(s, a) + \left| r + \gamma \mathbb {E}_{P(s'|s, a)}[\mathop {\max }_{a'} Q_{k-1}(s', a')] \right. \\&\left. - (r + \gamma \mathbb {E}_{P(s'|s, a)}[\mathop {\max }_{a'} Q^{*}(s', a')]) \right| \\&\le \delta _{k}(s, a) + \gamma \mathop {\max }_{a'} \mathbb {E}_{P(s'|s, a)} [\left| Q_{k-1}(s', a')- Q^{*}(s', a') \right| ]&\! \textcircled {2}\\&= \delta _{k}(s, a) + \gamma \mathop {\max }_{a'} \mathbb {E}_{P(s'|s, a)}[\zeta _{k-1}(s', a')] \end{aligned} \end{aligned}$$

where $\textcircled {1}: Q^{*} = \mathcal {T} Q^{*}. \textcircled {2}:$ Jensen’s Inequality.

Thus, $\zeta _{k}(s, a) \le \delta _{k}(s, a) + \gamma \mathop {\max }_{a'} \mathbb {E}_{P(s'|s, a)}[\zeta _{k-1}(s', a')]$. $\square$

Appendix B

The advantages of AWBB loss function over WQF loss function will be illustrated by a simple example shown in Fig. 11. Assume that the agent chooses the action a in state s and transfers to state $s'$. Meanwhile, the Q-function is estimated as $Q(s, a) = 3$. There are three next-step action choices $a_1, a_2, a_3$. In addition, we assume that there are three target Q-networks in the ensemble Q-network.

In Fig. 11, the OOD actions($a_1$ and $a_2$) are noted by the dotted line, and the red colour represents the $a_{ij} = \mathop {\arg \max }_{a_{ij}} Q^i(s', a_j). i = 1, 2, 3; j = 1, 2, 3$, where the superscript i is the i-th target Q-network, and the subscript j is the j-th action.

Fig. 11

A simple example to show the advantage of AWBB over WQF loss function

For simplicity, we assume that the reward $r=0$ and discount factor $\gamma =1$. According to the Bellman error $\delta (s, a) = \left| Q(s, a) - \mathcal {T} Q(s, a) \right|$, we calculate

$$\begin{aligned} \begin{aligned}&\delta ^1 (s, a) = \left| Q(s, a) - Q^1(s', a_1) \right| = \left| 3 - 12 \right| = 9, \\&\delta ^2 (s, a) = \left| Q(s, a) - Q^2(s', a_2) \right| = \left| 3 - 15 \right| = 12, \\&\delta ^3 (s, a) = \left| Q(s, a) - Q^3(s', a_3) \right| = \left| 3 - 6 \right| = 3. \end{aligned} \end{aligned}$$

Then, we assume that the attention weights after training are strictly inverse proportional to the Bellman error since the attention network should assign lower weights to the larger Bellman errors. Thus, the normalized attention weight of each target Q-network is calculated as follows,

$$\begin{aligned} \begin{aligned}&\alpha _1 = \delta ^1(s,a)^{-1} / \sum _{k=1}^{3} \delta ^k(s,a)^{-1} = 4/19, \\&\alpha _2 = \delta ^2(s,a)^{-1} / \sum _{k=1}^{3} \delta ^k(s,a)^{-1} = 3/19, \\&\alpha _3 = \delta ^3(s,a)^{-1} / \sum _{k=1}^{3} \delta ^k(s,a)^{-1} = 12/19. \end{aligned} \end{aligned}$$

For the WQF loss function $\mathcal {L}_{WQF}(s, a, s', \alpha )$, 7.69.6

$$\begin{aligned} \begin{aligned} \mathcal {L}_{WQF}(s,a,s',\alpha )&= \left[ \sum _{i=1}^{3}\alpha _{i}Q(s, a) - \mathop {\max }_{a_j} \sum _{i=1}^{3} \alpha _{i} Q^{i}(s', a_j) \right] ^2 \\&= \left[ 3 - \mathop {\max }_{a_j} \left[ \begin{array}{ccc} 4/19 \times 12 + 3/19 \times 12 + 12/19 \times 4 \\ 4/19 \times 9 + 3/19 \times 15 + 12/19 \times 4\\ 4/19 \times 6 + 3/19 \times 6 + 12/19 \times 6 \end{array} \right] \right] ^2 \\&= \left[ 3 - 132/19 \right] ^2 \\&= 5625/361. \end{aligned} \end{aligned}$$

For the form of AWBB loss function $\mathcal {L}_{AWBB}(s, a, s', \alpha )$, 79

$$\begin{aligned} \begin{aligned} \mathcal {L}_{AWBB}(s,a,s',\alpha )&= \sum _{i=1}^{3}\alpha _{i} \left[ Q(s, a) - \mathop {\max }_{a_j} Q^{i}(s', a_j) \right] ^2 \\&= 4/19 \times (3-12)^2 + 3/19 \times (3-15)^2 + 12/19 \times (3-6)^2 \\&= 6156/361 + 8208/361 + 2052/361. \end{aligned} \end{aligned}$$

Based on the example above, firstly, even though the attention weights are appropriately assigned to each target Q-network, we found that agent with $\mathcal {L}_{WQF}(s, a, s', \alpha )$ chooses $a_1 = \mathop {\max }_{a_j} \sum _{i=1}^{3} \alpha _{i} Q^{i}(s', a_j)$, which is an OOD action. Secondly, although the agent with $\mathcal {L}_{AWBB}(s, a, s', \alpha )$ chooses the OOD action $a_1$, $a_2$ to update the target Q-network $T-Q-Head_1$, $T-Q-Head_2$, respectively, the loss values for target Q-network $T-Q-Head_1$ and $T-Q-Head_2$ are 6156/361, 8208/361, larger than the $\mathcal {L}_{WQF}$, which means OOD actions causes a larger loss. Meanwhile, the agent with $\mathcal {L}_{AWBB}(s, a, s', \alpha )$ chooses the in-distribution action $a_3$ according to the $T-Q-Head_3$, which introduces a more minor error than $\mathcal {L}_{WQF}(s, a, s', \alpha )$. Therefore, using the $\mathcal {L}_{AWBB}(s, a, s', \alpha )$ is more consistent with the analysis of Theorem. 1.

Appendix C

Table 1 DQN Hypermaters to Build Datasets

Table 2 MetaDrive Setting Parameters

Table 3 Hypermaters in DQN, Ensemble, REM, Independent-AEM and AEM