Use of artificial intelligence techniques in characterization of vibration signals for application in agri-food engineering

Abstract

Bottling machinery is a critical component in agri-food industries, where maintaining operational efficiency is key to ensuring productivity and minimizing economic losses. Early detection of faulty conditions in this equipment can significantly improve maintenance procedures and overall system performance. This research focuses on health monitoring of gripping pliers in bottling plants, a crucial task that has traditionally relied on analyzing raw vibration signals or using narrowly defined, application-specific features. However, these methods often face challenges related to limited robustness, high computational costs, and sensitivity to noise. To address these limitations, we propose a novel approach based on generic features extracted through basic signal processing techniques applied to vibration signals. These features are then classified using a random forest algorithm, enabling an effective analysis of health states. The proposed method is evaluated against traditional approaches and demonstrates clear advantages, including higher accuracy in detecting and classifying faulty conditions, greater robustness against random perturbations, and a reduced computational cost. Additionally, the method requires fewer training instances to achieve reliable performance. This study highlights the potential of artificial intelligence and signal processing techniques in predictive maintenance, offering a scalable and efficient solution for fault detection in manufacturing processes, particularly within the agri-food sector.

1 Introduction

Maintenance strategies play a critical role in ensuring the reliability and efficiency of industrial systems. However, traditional approaches often fail to fully address the complexity of modern industrial environments, where real-time monitoring and predictive insights are essential. Key challenges include the high dimensionality of monitoring data, the imbalanced nature of datasets due to infrequent fault occurrences, and the lack of cost-effective solutions for comprehensive Health Monitoring (HM).

Defining a proper maintenance strategy of devices and systems or, in a broader sense, an Asset Management (AM), is a very hot topic with a huge impact on industry operation as it enhances performance, increases reliability, decreases time-down, and saves cost. An up-to-date state of the art of this topic can be found in [1].

For any type of organizations, developing an effective AM is a key factor to achieve value by balancing risks and opportunities, to attain an optimum trade-off between costs, risks, and performance [2].

Fig. 1

Maintenance maturity pyramid

In the context of AM, up to five levels in the maintenance of devices and systems are usually considered [3,4,5]: Reactive Maintenance (level 1), running until a failure and then repairing; Preventive Maintenance (level 2), cyclic inspection and conservation activities based on time or use; Condition-Based Maintenance (level 3), triggered by some rules (e.g. exceeding a certain threshold) based on objective measures obtained by several sensors; Predictive Maintenance (level 4), where actual sensor data about the equipment and its operating condition are extensively and continuously analyzed for a very early detection of potential malfunctioning, suggesting equipment or operating conditions modifications and predicting its Remaining Useful Life (RUL); and Risk-Based Maintenance (level 5), for an integral and comprehensive approach, considering assets performance, reliability, and costs. These maintenance maturity levels are depicted as a pyramid in Fig. 1.

This paper focuses on the three upper levels of the pyramid (highlighted in green), where Health Monitoring is essential. HM involves capturing data such as vibrations (accelerations), sounds, temperatures, voltages, and electric currents. These measurements are typically recorded as temporal signals or time series data, often sampled at a constant rate.

The field of industrial Health Monitoring (HM) has seen considerable advancements in maintenance strategies, encompassing rule-based systems, traditional Machine Learning (ML) techniques, and specialized feature extraction methods. Despite these advancements, existing methodologies face significant challenges, particularly in addressing the dynamic and resource-constrained nature of industrial environments. Rule-based systems [6], while conceptually simple, lack the adaptability to handle complex and variable fault patterns, often resulting in suboptimal performance in dynamic scenarios. Similarly, traditional ML techniques [7] typically rely on extensive labeled datasets to achieve high accuracy [8, 9]. However, the collection of such datasets in HM applications is time-consuming, costly, and impractical, as faults occur infrequently and datasets are often small and imbalanced.

Recent studies have explored data-driven and ML-based approaches as state-of-the-art solutions for analyzing high-dimensional HM signals [10]. However, few have addressed the critical trade-off between feature extraction complexity and performance in resource-constrained environments. For example, methods reliant on deep learning architectures often achieve superior performance but at the cost of significant computational and data requirements, which limits their practical applicability in real-world settings [11]. Similarly, many existing techniques fail to account for the robustness needed to handle noisy environments and diverse fault types, resulting in reduced reliability across applications.

A major limitation of existing data-driven methods is their inability to balance computational efficiency with classification accuracy. Approaches based on raw features, such as vibration signals comprising thousands of samples, yield high-dimensional datasets imposing excessive computational demands and often lead to overfitting when training ML models [12]. These issues are further exacerbated by the need for large and representative datasets, which are challenging to obtain in industrial contexts where faulty states are rare.

Conversely, specialized feature extraction methods are frequently designed for specific fault detection tasks [13], requiring deep domain expertise and significant computational resources. When a deep knowledge of the signal interpretation is available, very specialized features can be extracted applying specific signal processing algorithms. For instance, MPEG-7 [14] parameters or fine-tuned Mel Frequency Cepstrum Coefficients [15] for audio signals, State-of-Charge and State-of-Health related Key Performance Indicators (KPI) for battery description [16], or kurtogram-based attributes for rolling bearings [17]. While these methods may achieve high accuracy in controlled environments, their scalability and generalizability to diverse industrial settings are limited.

Fig. 2

Trade-off between classification and feature extraction efforts

On one hand, describing signals with raw features is the simplest extracting procedure but it yields to high-dimensional datasets, requiring a large number of instances and very demanding classification algorithms. On the other hand, characterizing signals by very specialized features drives to low-dimensional reduced datasets which are more easily classified, but at the cost of a large extraction effort which requires a deep engineering knowledge.

To address these limitations, this study introduces a novel methodology leveraging generic features for fault detection and classification. Generic features provide a middle ground between raw and specialized features, offering computational efficiency without sacrificing classification accuracy. This trade-off is depicted in Fig. 2. Unlike specialized features, they require minimal domain-specific knowledge and are inherently adaptable to various fault types. This innovation significantly reduces data requirements, computational complexity, and costs, making the methodology particularly well-suited for real-world applications where scalability, robustness, and efficiency are paramount. Moreover, the proposed approach demonstrates strong resilience to noise and variability, which are common in industrial environments, thereby enhancing its practicality and reliability.

In this approach, vibration signals are summarized by a reduced set of generic features, which are commonly extracted from the signal using time, frequency, or time-frequency domain analysis. Some more specific methods have also been proposed, based on Cepstrum [18], Wavelet Analysis [19], Hilbert-Huang Transform [20], Empirical Mode Decomposition [21], Linear Predictive Coding [21], Time Series Analysis [22], etc. A review of these feature extraction procedures has been described for different applications, such as mechanical vibrations [23], sounds [24] or biomedical signals [25].

The present paper studies the compromise between classification and feature extraction when the three previous defined types of features are used to detect faults in a particular industrial context. In the research, we focus on the input gripping pliers of the blow molding machine in a plastic bottling plant (detailed in Section 2.1), where the features must be extracted from vibration signals acquired by accelerometers (extraction process described in Sections 2.2, 2.3, and 2.4).

The analysis of the input gripping pliers serves as a critical case study, as their malfunction can disrupt the production line and contribute to inefficiencies. Understanding the relationship between feature extraction and classification accuracy in this context not only aids in fault detection but also underscores the broader implications for optimizing production systems. By addressing these challenges, this research aims to highlight how improved Health Monitoring (HM) can directly impact key performance indicators like overall equipment effectiveness (OEE), which remains a pressing issue in many industries.

The importance of this study relies on one hand, in the fact that the OEE in production companies is about 60% [26, 27]. The 40% loss of efficiency is mainly due to five factors: (i) planned stoppages, for planned maintenance or cleaning activities; (ii) machine failures, due to unexpected damages; (iii) short process failures (up to a few minutes), caused by jams or lacking products; (iv) process slowdown, where the equipment is not running at its optimum production rate; and (v), initialization procedures, to prepare the machine for a certain production process. Most of these factors can be significantly reduced with an adequate AM strategy, increasing the OEE and enhancing the overall economic results.

Also, the studied application is very significant as bottling plants are an essential element in the production phase of the beverage [28] and other agri-food products life cycle [29]. The food industry includes all activities (production, processing, manufacturing, sale, and distribution) of food, dietary supplements, and beverages [30]. In other words, the food industry includes all the stages of the process, from design to delivery of the product to the customer, through design, construction, and maintenance, in the animal nutrition industry and the food industry [31].

The primary contribution of this research is the demonstration that, in the studied industrial setting, a set of generic features offers superior performance compared to both raw, unprocessed features and highly specialized, knowledge-based attributes. Unlike raw or highly specialized features, generic features achieve a significantly higher classification accuracy with much lower computational demands. This advantage is particularly noteworthy in fault type identification, where generic features outperform specialized attributes, which, while effective for general fault detection, show limited capability in pinpointing specific fault causes.

Furthermore, generic features prove to be more resilient to noise, maintaining classification performance even in datasets with random noise contamination, a limitation observed in raw and specialized features. Another important contribution is the reduction in dataset size requirements; classifiers trained with generic features need far fewer data points, making this approach more practical and cost-effective for industrial applications.

Additionally, the research highlights the advantage of dividing vibration signals into smaller segments, thereby increasing the number of training examples and improving classification performance, with an optimal segment length identified to balance representational accuracy and instance availability.

By advancing the understanding and application of generic features, this study contributes to bridging critical gaps in HM methodologies. It offers a scalable, efficient, and robust solution that addresses the key shortcomings of existing approaches while enabling more effective fault detection and classification. These contributions mark a significant step forward in the field, particularly for resource-constrained industrial systems requiring practical, high-performance HM solutions.

The remaining of the paper is organized as follows: Section 2 describes the engineering application of the research (a bottling system), their health conditions, the dataset generation process and the classification algorithm proposed; Section 3 presents the results obtained by applying three types of features (raw, specialized and generic); Section 4 discusses these results analyzing the impact of perturbations on datasets, the number of training instances, the length of vibration signals and the required computational effort; and, finally, Section 5 states the main conclusions of the article.

2 Methodology

2.1 The bottling system

A bottling plant for filling beverages is a set of several very different types of specialized machines and conveyors that automatically handles the entire process from pallets supplied with boxes containing empty bottles to the final output of pallets with (clean) boxes and filled and labeled bottles [32].

The bottling process can be abstracted as a discrete sequence of operations aimed at transforming raw materials into a finished product ready for distribution. Let $S={s_1,s_2.\cdots ,s_n}$ represent the set of sequential stages in the bottling system, where $s_i$ denotes the i-th process, and n is the total number of stages. Each stage involves an input state $b_{i-1}$, a transformation $f_i(b_{i-1})$, and an output state $b_i$. Mathematically, the system can be expressed as:

$$\begin{aligned} b_i=f_i(b_{i-1}),i=1,\cdots ,n \end{aligned}$$

(1)

where $b_0$ is the raw material input and $b_n$ represents the final output, i.e., packaged and palletized bottles. The goal of this work is to implement a health monitoring system for critical components $C \subset S$, ensuring operational reliability and efficiency.

Specifically, the bottling system under investigation consists of the following processes:

• 1. Input Stage ($s_1$): A conveyor belt delivers raw plastic preforms ($b_0$) to the system (state $b_1$).

• 2. Heating Stage ($s_2$): An oven heats the preforms to a temperature sufficient for blow molding, transforming the preforms into a deformable state $b_2$.

• 3. Transfer Stage ($s_3$): Gripping pliers transfer the heated preforms to the blow molding machine (state $b_3$).

• 4. Blow Molding Stage ($s_4$): The blow molding machine applies a shaping force to form the final bottle structure $b_4$.

• 5. Intermediate Transfer ($s_5$): Gripping pliers transfer the bottles to the filling machine (state $b_5$).

• 6. Filling and Capping Stage ($s_6$): The bottles are filled with a target liquid volume and capped (state $b_6$).

• 7. Packaging Stage ($s_7$): The bottles are grouped into packages (state $b_7$).

• 8. Palletizing Stage ($s_8$): Packages are stacked onto pallets for distribution, ensuring a spatial arrangement that maximizes stability during transport (state $b_8$).

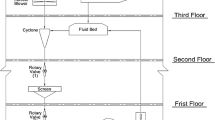
The health monitoring system, indicated in gray in Fig. 3, focuses on critical stages $C=\{s_3,s_4,s_5\}$, particularly the gripping pliers, which are prone to wear and mechanical failures. These components operate under thermal and mechanical conditions that are monitored using specialized sensors. Fig. 3 illustrates the system layout, highlighting cold parts (blue), hot parts (orange), and health monitoring system integrations (gray). By generalizing the system’s operations using the above formulations, the methodology can be adapted to a wide range of bottling processes beyond the specific implementation described here.

Fig. 3

Bottling system diagram. Cold parts (blue), hot parts (orange), and health monitoring (gray)

Fig. 4

Diagram of the mechanical system controlling position and opening of the input gripping pliers. The most mechanically demanded elements are colored in orange

The gripping pliers are embedded in a mechanical system with several moving parts, where the plier’s position is controlled by a rotating motor linked through a bearing, and the opening of the plier’s arms is driven by a cam coupled by a spring. Four gripping pliers, at a 90°angle, are linked to the rotating motor through a rod (see Fig. 4). The bottles arrive at a nominal rate of 7200 pieces per hour (120 per minute) which means that motor rotates at 30 rpm (4 bottles are managed in each revolution). The operation at an increased rate of 9200 bottles per hour (bph) has also been tested (the motor rotating at 38.3 rpm).

In this arrangement the most mechanically demanded elements are the bearings (supporting a continuous high-speed friction) and the springs (suffering repetitive cycles of stretching and compression). Additionally, the input gripping pliers (showed in Fig. 5) suffer increased wear and tear as they operate at slightly higher temperatures than the output counterparts. Therefore, the focus of this research will be in those elements. A more detailed description of the bottling system and the studied elements can be found in [33].

Fig. 5

Input gripping pliers of a bottling system

The hypothesis of this work is that possible damages in any of the elements under supervision (bearings or springs), will yield a different pattern of mechanical vibrations. To explore this postulate, a single axis accelerometer is attached to the pliers’ structure measuring de vibrations in the radial direction (orthogonal to the rotation axis). More complex faults may necessitate monitoring across multiple axes; however, these scenarios are beyond the scope of our study. Since the vibration signals (both healthy and faulty) have a bandwidth of approximately 5.5 kHz, sensor values are acquired at a rate of 12.8 kHz. This rate exceeds twice the bandwidth and is among the sampling options available in the data acquisition equipment described in [33].

Table 1 Experiments and segments for each health state

A bottling machine, typical of those used in bottling plants, was tested across 13 experiments conducted over multiple days under controlled conditions. The machine was evaluated under three health conditions: in four experiments (1 to 4), it operated in a healthy state; in five experiments (5 to 9), a spring damage (SD) fault was introduced; and in the remaining four experiments (10 to 13), a bearing damage (BD) fault was induced. Each experiment lasted approximately 3 minutes.

2.2 Raw features

Considering each experiment an instance (example) in a machine learning approach, their number (4 or 5 of each class) are clearly insufficient for a data-driven classification. Therefore, each experiment is split in 5-seconds segments which obtains 497 hundred instances (instead of the original 13). The number of segments in each class is detailed in Table 1. The value chosen for the segment duration (five seconds) is discussed in Section 4.5.

The number of values (features in ML terminology) characterizing each 5-seconds segment is 64000, a figure directly derived from the 12.8 kHz sampling rate. This is a high dimensional vector that poses a special challenge for classifier algorithms.

Fig. 6

Examples of vibration signals for each health state. Acceleration units are expressed in terms of g (9.81 m/s$^{2}$)

Fig. 7

Overview of the process to extract the kurtosis-based specialized feature

Fig. 8

Example of spectra for a vibration signal. Left: Original healthy signal (blue), and the result after filtering (orange), and envelope detection processes (green). Right: Spectra of the envelope signal corresponding to three different health states

A graphical representation of the vibration signals is depicted in Fig. 6, for examples of each health state. This time-domain representation seems quite confusing and, at a first glance, no definitive conclusion about the corresponding health state can be easily reached. Then, another set of features representing vibrations must be explored.

2.3 Specialized features

As the high dimensionality of raw vectors may cause special complexities to the ML algorithms, specially is the number of instances is not too large, alternative features are considered. In a general case, the deep knowledge of the engineering process yielding the vibration signals, can be used to design a very short set of highly specialized features that summarize the health state of the system. For the input gripping pliers of the bottling machine, these summarizing features are derived from the hypothesis–initially inspired by [33]–that the system behaves similarly to a rolling bearing, an assumption later validated through this research. This approach leverages the extensive body of knowledge on rolling bearings, which have been widely studied for health monitoring purposes [34]. Specifically, the specialized features proposed here are primarily based on kurtosis, as defined in [35] and [17].

The process to obtain these features begins with band-pass filtering of the vibration signal, followed by envelope detection and calculation of the statistical kurtosis of the resulting values. This sequence is repeated across a range of filters, selecting the filter that produces the highest kurtosis as the optimal choice, with this kurtosis value serving as the feature characterizing the vibration. To provide a clearer understanding of the workflow and its connection to the paper’s outcomes, Fig. 7 offers an overview of the process and references Figs. 8 to 11 to highlight their interrelation.

In more detail, for each vibration segment, defined as a signal v(t), a band-pass filtered signal r(t) is obtained for a filter in the frequency range $[f_c-b_c,f_c+b_f]$, where $f_c$ is the central frequency and $b_c$ the semi-bandwidth of the filter. Then, the envelope e(t) of the filtered signal r(t) is derived. Since envelope detection of a signal is some sort of demodulation of an Amplitude Modulated signal, the envelope e(t) is centered at zero-frequency and has bandwidth $b_f$. The spectrum of the vibration, filtered, and envelope signals are depicted in the left panel of Fig. 8 for a healthy experiment. In the right panel, the envelope’s spectra of different health conditions are compared.

The time-domain representation of the envelope signal is depicted in Fig. 9 for segments with different health conditions.

Once the envelope signal e(t) has been obtained, its samples are statistically analyzed and its kurtosis derived using the following expression,

$$\begin{aligned} k(f_c,b_f)=\dfrac{1}{N}\sum ^{N}_{i=1}{(\dfrac{e_i-\mu _e}{\sigma _e})^4} \end{aligned}$$

(2)

where $e_i$ is the value of the $i^{th}$ sample of the e(t), $\mu _e$ and $\sigma _e$ are the mean and standard deviation of the values of e(t), and N is the total number of samples in the segment. The probability density functions of the samples of e(t) for different health states are depicted in Fig. 10. They have been obtained using a kernel density estimation technique.

The value of the kurtosis is a function of the parameters of the filter, $f_c$ and $b_c$. This relationship is drawn as a heat-map in Fig. 11 for a certain segment.

Fig. 9

Envelope signals for vibrations corresponding to different health conditions

Fig. 10

Statistical distribution of the samples of the envelope signals, for vibrations corresponding to different health conditions

Fig. 11

Kurtosis of the envelope of a filtered vibration signal, for different values of the filter’s parameters: central frequency $f_c$, and bandwidth $b_f$

The kurtosis feature K is defined as the maximum value of the kurtosis $k(f_c,b_f)$, that is,

$$\begin{aligned} K = \max _{f_c,b_c}{k(f_c,b_c)} \end{aligned}$$

(3)

For the segment represented in Fig. 11, the maximum value is $K = 174$, obtained for an optimum band-pass filter centered at $f_c^* = 3936Hz$ with a semi-bandwidth $b_f^*=202Hz$. When the optimum filter is applied to a segment, an optimum filtered signal and an envelope signal are obtained, denoted as $r^*(t)$ and $e^*(t)$ respectively.

From the previous process, a companion feature can also be obtained, the Root Mean Square (RMS) of the optimum envelope $e^*(t)$. It can be defined as:

$$\begin{aligned} R = \sqrt{\dfrac{1}{N}\sum _{i=1}^N{e_i^*}^2} \end{aligned}$$

(4)

Using this approach, the number of features characterizing each segment is just two (kurtosis and RMS), which is a very low dimensional vector, quite convenient for ML algorithms.

2.4 Generic features

The specialized features described in the previous section obtains a very low-dimensional description of the vibrations but requires a significant extraction process (computationally expensive) and, even more important, a deep knowledge of the underlying engineering process. In fact, the proposed features have been derived from the field of rolling bearings, but do not consider the unknown engineering details of other faults, such as those concerning the springs.

An alternative, intermediate between raw and specialized features, is to use a reduced set of generic features which are not tailored for any known engineering process. In the case of time signals, they are derived analyzing the vibrations both in the time-domain and in the frequency-domain. The set of generic features used in the paper are inspired in those used for some other authors [36,37,38].

Table 2 Definition of time-domain generic features

The process of feature extraction assumes that the vibration signal v(t) is sampled at a certain rate obtaining a sequence of N ordered values, where the $i^{th}$ sample is denoted as $v_i$. Then. in the time-domain, up to 24 features are defined, as it is described in Table 2.

In this time-domain set of features, $T_{12}$ resembles the specialized kurtosis defined in (2) and (3), and $T_7$ looks like a scaled version of the RMS defined in (4) but they are not the same, since generic features are obtained from the original vibration signal while the specialized attributes are derived from the envelope signal.

Applying the Fast Fourier Transform to a vibration signal, its power spectrum is obtained in the form of a sequence of M ordered values, where the j-th element denoted as $V_j$, corresponds to the power of the harmonic component at the frequency $f_j$. By the Nyquist-Shannon sampling theorem, the number of values in the power spectrum is one half of the number of samples, $M=N/2$. Then, in the frequency-domain, up to 9 features have been defined, as it is described in Table 3.

Table 3 Definition of frequency-domain generic features

Using this approach, the number of generic features characterizing each segment is 33. This means that the dimensionality of the vector describing each vibration segment, while not low, is certainly quite moderate.

2.5 Design matrices

The segments of vibrations obtained from the experiments described in Table 1, can be characterized using three different strategies: raw, specialized, and generic features. So, the design matrices corresponding to each approach has the same number of rows (497, one for each 5-seconds length segment), but different number of columns (features).

To tune the ML model, the rows of the design matrix are split into 3 groups using a hold-out technique: training (60%, 298 instances), to obtain the parameters of the ML model; validation (20%, 99 instances), to select the hyperparameters of the model; and testing (20%, 100 instances), to generalize the results of the model to data not used in its construction. The number of rows in each design matrix corresponds to the count of observations. The number of columns, however, depends on the feature set used in each scenario: 64,000 columns for raw features (5-second recordings sampled at 12.8 kHz), 2 columns for specialized features (kurtosis and RMS), and 33 columns for generic features (as outlined in Tables 2 and 3). The structure of the corresponding design matrices is summarized in Table 4.

Table 4 Structure of the design matrices

For a given vibration segment, the values of its corresponding features can significantly differ from each other, leading to a convergence problem in many ML algorithms. To avoid it, the design matrix is usually normalized by column before its use for training. In this research a z-score normalization has been employed. For a design matrix X of dimension ($n \times d$), the value of the i-th row and j-th column is normalized using the expression:

$$\begin{aligned} Z_{i,j} = \dfrac{X_{i,j}-\mu _{xj}}{\sigma _{xj}} \end{aligned}$$

(5)

where $\mu _{xj}$ and $\sigma _{x_j}$ are the mean and standard deviation of the values in the j-th column, that is,

$$\begin{aligned} \mu _{xj} = \dfrac{1}{n}\sum _{i=1}^n{X_{i,j}}, \sigma _{xj} = \sqrt{\dfrac{1}{n}\sum _{i=1}^n(X_{i,j}-\mu _{xj})^2} \end{aligned}$$

(6)

To extend the research to more demanding scenarios, some synthetics design matrices are derived from the original ones by adding some random noise. The value of the i-th row and j-th column of the noisy synthetic design matrix is obtained using the expression, $W_(i,j)=Z_(i,j)+G_(i,j)$, where G is a random gaussian matrix of dimension ($n \times d$), null mean, and standard deviation $\sigma _N$, also known as noise level.

2.6 Classification algorithm

The ML algorithm requires, not only a design matrix, but also a target (column) vector, y, of dimension ($n\times 1$), where the value at the i-th row corresponds to the health state of the i-th vibration segment. As there are only three different values of the health state (see Table 1) and they are nominal (no order between them can be established), the ML algorithm must face a classification problem.

Many classification algorithms have been proposed. As the purpose of this research is to compare different ways of describing vibrations and not classification algorithms, a particular classifier has been selected: the random forest classifier [39], which can work in non-linear problems, has a very limited number of hyperparameters, outperforms many other algorithms when datasets have a low number of instances, and its predictions can be very well generalized as it contains an ensemble of underlying decision trees.

The computing tasks in the research have been coded in Python, while the ML algorithms and, in particular, the random forest classifier, have been programmed using the scikit-learn library [40]. The random forest classifier uses the default options in that library but two of them are used to tune the model. These two hyperparameters are: the number of decision trees in the forest; and the maximum depth of every tree. This later one plays the role of regularization hyperparameter, avoiding overfitting to training data.

The performance of a certain classification algorithm can be revealed by the absolute confusion matrix, where the element $A_{kq}$ of this matrix represents the number of instances belonging to the k-th class, that has been classified as belonging to the q-th class. It is also common to represent the algorithm’s performance in terms of classification ratios by using the relative confusion matrix, where the element $CM_{kq}$ is obtained as

$$\begin{aligned} CM_{kq} = \dfrac{A_{kq}}{n_k} \end{aligned}$$

(7)

being $n_k$ the number of instances belonging to the k-th class.

To summarize the confusion matrix in a single value, several classification metrics have been proposed. Probably the most used one is the classification’s accuracy ACC defined as

$$\begin{aligned} ACC = \dfrac{1}{n}\sum _{k=1}^C{n_k}{CM_{kk}} \end{aligned}$$

(8)

where C is the total number of classes. This metric is easy to understand, has a good behavior under slightly imbalanced datasets [41] and it is not affected by a change in the order of the classes [42].

3 Results

3.1 Classification using raw features

As it was described in Section 2.2 and summarized in Table 4, each vibration segment can be featured using 64000 raw values. This high-dimensional vectors can be graphically represented by applying a Principal Component Analysis (PCA) [43]. This technique rotates the vectors using a linear transformation that maximize statistical variance in the first components of the new vectors. Then the transformed vector is projected onto the plane of the two first components, obtaining a 2D representation. The result, indicating with colors the different health states, is shown in Fig. 12. From this figure, we should expect a quite good separation of classes but with some overlaps leading to a few misclassifications.

Fig. 12

Bidimensional representation of the vibration dataset using raw features and a PCA dimensionality reduction technique

To select the two hyperparameters of the random forest classifier several combinations of the number of trees and their maximum depth have been explored. The classification accuracy on the validation dataset for these combinations is depicted in Fig. 13. An ensemble of 75 trees with a maximum depth of 30 steps between the root node and the leaf node have been selected as the hyperparameters of the classifier.

Fig. 13

Classification accuracy as a function of the values of the hyperparameters: maximum depth of trees (left) and number of tress (right)

After training the model with these hyperparameters, the classification results obtained on the testing dataset are shown as a confusion matrix shown in Fig. 14, with an overall accuracy of 83%.

Fig. 14

Confusion matrix for the random forest classifier with segments defined by raw features

3.2 Classification using specialized features

In the case of using the two specialized features described in Section 2.3, , kurtosis and RMS, the graphic representation of the segments in the dataset is straightforward, as it is shown in Fig. 15. As the range of values for kurtosis is very large, they have been represented in logarithmic scale. From this figure, a very good identification of healthy vibrations should be expected. In fact, using only the kurtosis feature, most of the healthy segments are correctly separated. However, the two types of damages (on bearing and spring) are very overlapped, suggesting a difficult separation of these two faulty classes.

Fig. 15

Bidimensional representation of the vibration dataset using specialized features. Kurtosis values are in logarithmic scale

A clearer view of the overlapping of the feature values can be seen using the probability density function (PDF) of these values as they are depicted in Fig. 16. By using just kurtosis, healthy segments appear very well separated from faulty ones, but the pdfs of the faulty conditions are significantly overlapped. On the other hand, RMS values could help to separate the faulty segments, but a limited success should be expected as their PDFs are still considerably overlapped.

Fig. 16

Probability density functions corresponding to the specialized features: kurtosis (left) and RMS (right)

A random forest classifier has been selected and trained using these specialized features. The best results on the validation datasets have been obtained for the same values of the hyperparameters indicated in the previous Section. And the classification results are drawn as a confusion matrix in Fig. 17, with an overall accuracy of 88%. It can be seen that healthy segments are successfully identified in a 100% of the cases, but identifying the type of fault is a much harder task for this classifier.

Fig. 17

Confusion matrix for the random forest classifier with segments defined by specialized features

3.3 Classification using generic features

Finally, if the vibration segments are defined using the 33 generic features defined in Section 2.4, the dataset can be graphically represented using PCA as it is depicted in Fig. 18. A cleaer separation of classes can be observed, which suggest that classification algorithms should obtain very good results.

Fig. 18

Bidimensional representation of the vibration dataset using generic features

The classification results obtained by the random forest classifier using the generic features are represented in Fig. 19. A 100% success rate have been obtained clearly overperforming the other two ways of featuring vibration signals.

Fig. 19

Confusion matrix for the random forest classifier with segments defined by generic features

Fig. 20

Confusion matrices for the random forest classifier with segments defined by three types of noisy features (noise level $\sigma _N=1$): raw (left), specialized (center) and generic (right)

Fig. 21

Classification performance as a function of the noise level added to the original dataset: accuracy (left); loss of accuracy (right)

4 Discussion

The results described through Section 3 show that, for the analyzed dataset, the description of vibrations by generic features clearly outperforms the other two alternatives: raw or specialized features.

In this section the impact on performance of four issues will be discussed: synthetically generated noisy features, number of training instances, length of vibration segments and computational effort of each method.

4.1 Noisy features

To extend the study’s conclusions beyond the original datasets, a synthetic modification of the design matrices, as described in Section 2.5, was performed. First, each feature value was normalized to achieve a mean of zero and a standard deviation of $\sigma =1$. Gaussian noise with a mean of zero and a standard deviation of $\sigma _N$ was then added. For $\sigma _N$, classification performance significantly decreased: overall accuracy dropped by 26 percentage points (from 83% to 57%) for raw features, 52 percentage points (from 88% to 36%) for specialized features, and 14 percentage points (from 100% to 86%) for generic features.

Confusion matrices for these three types of features are shown in Fig. 20. It must be noted that a classifier making a random guess of one out of the three possible classes should obtain on average an accuracy of 33.3%, a close value to the result obtained when specialized features are used.

It can be seen that the use of generic features not only obtains the best accuracy results in the original datasets, but they are also the most robust features under noise perturbations. These results can be extended to different noise levels showing that accuracy of models using generic features worsen more slowly than those based on raw or specialized features, as it is depicted in Fig. 21.

To evaluate the noise robustness of each feature set, we define the Half-Accuracy Noise Threshold (HANT, $\sigma _{N_{50}}$) as the noise level that reduces the accuracy by half. For each line in Fig. 21, which depicts the function $acc=(\sigma _N)$ for a given feature set, it holds that $acc=( \sigma _{N_{50}})= acc(0)/2$. The values obtained for each feature set are shown in Table 5. The results indicate that generic features demonstrate greater resilience to noise compared to specialized features, with raw features occupying an intermediate position between the two.

4.2 Alternative techniques

As part of the research, various alternative approaches have been explored, including strategies to address dataset imbalance, the evaluation of different sets of generic features, and an analysis of the impact of using various classifiers.

First, to address the slight class imbalance in the dataset, the Synthetic Minority Over-sampling Technique (SMOTE) [44] was initially applied to increase the instance count of each class to match that of the most populated class. However, as the imbalance was small and SMOTE yielded no significant improvement, the study proceeded without synthetic instances.

Table 5 Noise robustness for each feature set

Second, in addition to the generic features listed in Tables 2 and 3, two additional feature sets were analyzed: one proposed by Nayana [45], based solely on time-domain characteristics, and another introduced by Yan [46], which incorporates statistical metrics from both time and frequency domains. The results, presented in Fig. 22, show that all generic feature sets outperform both specialized and raw features, with the feature set proposed in this research achieving the best performance among all.

Fig. 22

Accuracy vs. noise level added for other generic feature sets

Finally, additional classifiers were tested, including logistic regression, support vector machines (SVM), and various configurations of feedforward neural networks. While these models showed similar accuracy for both specialized and generic features, the high dimensionality of raw features presents a significant challenge for classification. As a result, performance varies noticeably, depending heavily on the classifier type and its hyperparameters. Among these algorithms, logistic regression had the lowest computational cost, followed by SVM and random forest with moderate requirements, while the neural network configurations were the most computationally demanding.

4.3 Bottling speed

All acquired vibration signals include bottling speed as associated information. However, this information was intentionally excluded as a feature in the design matrices for the three classification approaches (using raw, specialized, and generic features). Instead, only features derived from the vibration signal itself were used. This choice was based on the observation that bottling speed information is inherently embedded in the other features. For example, a PCA representation of the dataset using raw features, as shown in Fig. 23, reveals that instances with different bottling speeds occupy distinct regions, indicating that just two principal components are sufficient to differentiate the corresponding bottling speeds.

Fig. 23

Learning curves. The accuracy of the random forest classifier using different set of features is plotted as a function of the number of examples used to train the model

Classification accuracy under varying noise levels was also evaluated for the three feature types, both with and without including bottling speed as a feature. The results, shown in Fig. 24, indicate that incorporating bottling speed in the design matrices has a negligible effect on accuracy. This aligns with expectations, as bottling speed is inherently embedded in the other features, rendering it non-essential for accurately identifying the health state.

Fig. 24

Classification accuracy as a function of noise level added to the original dataset, evaluated across different feature types, with and without bottling speed as an additional feature

Fig. 25

Learning curves. The accuracy of the random forest classifier using different set of features is plotted as a function of the number of examples used to train the model (for two noise levels)

4.4 Learning curves

As it was described in Section 2, the vibration signal obtained in each experiment is split in many 5-seconds segments to increase the number of examples available to train the ML models. To check if the resulting number of segments are enough, the corresponding learning curves are depicted in Fig. 25, where each plot represents the evolution of the classification accuracy as the number of training examples is increased.

It can be concluded that the random forest classifier using generic features on a dataset with no added noise requires just 50 examples to achieve the maximum accuracy, while the use of the specialized features requires about 175, and the use of raw features do not get the maximum accuracy for the available training samples (the blue line does not stabilize for the range of available training instances). In the case of adding a noise level $\sigma _N=1$, the classifier using generic features requires 125 instances, that based on specialized features needs about 200, while the use of raw features appears to require more instances that those available in the training dataset. By performing more experiments and/or increasing their duration, the classifiers based on raw features would probably increase its accuracy even over the specialized features.

4.5 Length of segments

The number of examples to train the models could be easily increased by reducing the length of each segment. The intuition says that a very short segment may not be representative enough of its health condition and, therefore, classifiers trained on that segments will show lower performance.

On the other hand, choosing very long segments yields to a very scarce training dataset which certainly will affect the classifier performance as it was shown in the previous Section. Additionally, as the testing dataset will also be very scarce, the value of the accuracy will have a large variance.

Then, a balance must be sought about the length of the segments: nor too short under-representative signals, nor too long but scarce instances. To explore this balance, the classification accuracy has been computed using different length of segments. The results are depicted in Fig. 26 for the three types of features using the original dataset (no noise), and a perturbed datasets with a noise level of $\sigma _N=1$. It can be seen that short segments (leftmost part of the plots) show comparatively low accuracy, while long segments (rightmost part of the plots) also have low accuracy with values very spread (large variance due to the scarcity of testing instances). A trade-off can be reached for segments of 5-seconds length, as it is indicated in the figure, justifying the election made in Section 2.4.

Fig. 26

Classification accuracy for different segment lengths. The 5-second length selected for this research is depicted as a red dotted line

Fig. 27

Classifier accuracy using single features

Splitting signals to increase dataset size is a scalable methodology suitable for handling very long signals. The optimal segment length, however, is application-specific and should be tailored to each case. For example, in [47], the authors work with one-year-long signals, which they segment into one-day intervals. From a computational standpoint, splitting is highly efficient, as feature extraction becomes less costly with shorter segments. Overall, the computational impact of splitting is minimal.

4.6 Explaining the Overperformance of Generic Features

As demonstrated in the results section, the generic features proposed in this research consistently outperform the specialized features, which are primarily based on kurtosis. This outcome remains consistent even when alternative sets of generic features are employed, as shown in Section 4.2. Here, we will delve into the possible reasons behind these findings.

To begin, let’s examine the random forest classifier’s accuracy in identifying the health state condition when only a single feature—either specialized or generic—is used. The results, shown in Fig. 27, reveal that the carefully crafted kurtosis-based specialized feature achieves accuracy well above the mean. However, it performs at a level similar to several generic features, such as $T_9$, $T_{12}$, and $F_2$. This suggests that, for our application, the lengthy design and time-consuming extraction process of the kurtosis-based feature does not yield a significant advantage over certain off-the-shelf generic features.

Next, consider the correlation of the kurtosis-based specialized feature with other features, as measured by the absolute value of Pearson’s correlation coefficient. In Fig. 28, the blue line represents the kurtosis-based feature’s correlation with other features, while the orange line represents the root mean square (RMS)—a companion specialized feature. RMS offers a distinct perspective of the vibration signal, demonstrated by its low correlation with kurtosis, which can enhance feature diversity. Interestingly, other generic features also exhibit low correlation with kurtosis while achieving better performance in single-feature classification (e.g., $T_9$, $F_2$, and $F_3$), making them potentially more valuable complements to the kurtosis-based specialized feature.

Fig. 28

Absolute Pearson’s correlation of kurtosis (blue) and RMS (orange) with other features

Finally, we explore the cumulative accuracy achieved by classifiers as more features are added, using the Forward Feature Selection (FFS) algorithm [48]. In the first step, $T_{12}$ is chosen, as it yields the highest accuracy in Fig. 27. Adding $F_4$ further improves performance. This process is iteratively repeated until all features are considered, as shown in Fig. 29 (blue line). For comparison, we also conducted the same process starting with the kurtosis-based specialized feature, followed by the remaining features in sequence; this result is depicted by the orange line. In both cases, accuracy stabilizes around 15 features, suggesting that the superior results of the generic features are not attributable to any single optimal feature. Instead, they reflect the cumulative contribution of various features, each providing complementary insights into the vibration signals.

Fig. 29

Classifier accuracy with incremental feature selection using Forward Feature Selection: generic features (blue) vs. kurtosis-based plus remaining features (orange)

A hunting analogy illustrates this concept: to catch elusive prey, a shotgun firing multiple pellets—each with slightly diverging trajectories—is often more effective than a single, high-precision bullet. This analogy underscores the advantage of using a broad set of generic features over a limited set of specialized ones, a principle that appears to be domain-independent. Similar benefits have been observed in industrial applications like battery health monitoring [47] and various other classification contexts [49, 50].

4.7 Computational cost

In previous Sections, the three types of features have been analyzed from the perspective of their performance, as they are measured by the classification accuracy. However, the computing effort required by each method should also be considered. This effort can be broken down into three categories: extraction, training, and testing.

The extraction time considers the processes required to convert a 5 second vibration signal to a vector of raw, specialized, or generic features. In the case of raw features, no process is required, as the 64,000 values of the vibration (sampling rate of 12.8 kHz) already are the raw features.

Fig. 30

Computing times for different processes using raw, specialized, and generic features: feature extraction (left), model training (center), and classifier testing (right)

In the other hand, to extract the specialized features it is required to filter the signal, to get its envelope and then compute its kurtosis and RMS values (see Section 2.3). This process must be repeated for a grid of parameters of the filter, combining pairs of values for central frequency $f_c$ and bandwidth $b_f$. The specialized features have been extracted using a grid of $50\times 50$ pairs of values, which is a very time-consuming process.

Finally, the extraction of generic features implies making some calculations on the raw values to obtain the time-domain features, computing the spectrum of the signal using a Fast Fourier Transform (FFT), and eventually deriving the frequency-domain features from the spectrum values (see Section 2.4).

Once the design matrix has been constructed, its training portion is used to obtain the parameters defining the classifier. And finally, the time required to classify the instances in the testing dataset is analyzed. Usually, longer feature vectors drive to more computing costs on training and testing. Extraction, training, and testing costs have been measured using a Python 3 script running in a desktop computer powered by an Intel®i7-11700 processor at 2.10 GHz, under a Windows-11 operating system. The resulting computing times are shown (in logarithmic scale) in Fig. 30

Using raw features means no extraction effort but the corresponding longer feature vectors require significant training and testing times. Alternatively, specialized features demand very heavy computing for extraction (highly dependent on the grid size used to determine the optimum filter), but they have the shortest training and testing times due to the low dimensionality of the feature vectors. Finally, generic features are relatively easy to extract while its use for training and testing demands slightly higher computing resources than the specialized features.

These results demonstrate that both raw and generic features are suitable for real-time environments, as the extraction and prediction (testing) times are well below the segment duration (real-time training is not required). However, the extraction time for specialized features on a high-end laptop approaches the segment duration, presenting a significant challenge for real-time implementation on low-cost edge devices.

These values can be redrawn to replicate with actual data, the sketch depicted in Fig. 2. For this purpose, the classification effort will be assimilated to the sum of training and testing computing times. Results are shown in Fig. 31.a where the specific values are the center of the ellipses corresponding to each type of feature. Additionally, the computational effort (the sum of extraction, training, and testing times) associated to each features type can be compared to the classification accuracy obtained for that type, as it is depicted in Fig. 31.b. Raw and specialized features have a similar classification performance at a comparable computational costs, while generic features clearly overperforms both of them requiring a much lower effort.

Fig. 31

Summary of computational effort: left (a), trade-off between classification and feature extraction efforts for the actual data of this research; right (b), classification accuracy and computational effort

4.8 Implementation and scalability considerations

The integration of AI-based health monitoring with existing maintenance workflows in bottling plants presents opportunities to transition from preventive to predictive maintenance strategies. Unlike traditional preventive maintenance, which operates on scheduled intervals, predictive maintenance leverages real-time anomaly detection to address emerging issues proactively. By identifying subtle signs of wear or malfunction in gripping pliers, the proposed AI system allows maintenance teams to plan interventions more strategically, aligning with production goals of minimizing unscheduled downtime and enhancing equipment reliability.

However, deploying this solution at scale involves several practical challenges. One of the primary considerations is the installation and positioning of sensors on all relevant equipment, which could be logistically demanding and may necessitate wireless solutions to reduce operational disruptions. Furthermore, the high data throughput required for real-time monitoring could strain existing network infrastructure, especially if additional critical assets are to be monitored. Approaches such as edge computing or selective monitoring of high-priority assets may mitigate data handling challenges, facilitating smoother implementation at scale.

Compatibility with existing IT infrastructure is another critical aspect, as data integration between new AI systems and legacy maintenance frameworks can be technically complex. To address this, middleware solutions or APIs designed for seamless data interoperability can enhance integration, ensuring that the AI-driven system communicates effectively with established control systems. Additionally, data security is paramount, as real-time data processing and AI-driven maintenance introduce cybersecurity vulnerabilities. Industry-standard security practices, such as data encryption and role-based access control, are recommended to safeguard sensitive operational information and maintain system integrity.

From an operational standpoint, workforce considerations are essential for successful adoption. Implementing an intuitive user interface and providing training for interpreting AI-driven insights could improve usability for maintenance technicians unfamiliar with AI systems. Moreover, establishing a feedback loop with plant operators can further refine the model, allowing the system to adapt to the specific conditions and operational rhythms of individual plants.

The long-term implications of deploying this AI health monitoring system extend to both economic and operational benefits. By enhancing equipment uptime and reducing reactive maintenance, the system has the potential to yield a significant return on investment (ROI) over time. Future research should focus on validating the system’s effectiveness across various agri-food production environments and exploring its application to other critical equipment. Studying the system’s performance under diverse operational conditions would provide a more comprehensive understanding of its broader industrial applicability and impact.

5 Conclusions

The main finding of this research is that, for the analyzed industrial application, the use of a set of generic features clearly overperforms the other two alternatives: either raw unprocessed features or highly treated over-specialized knowledge-rooted attributes. Its classification accuracy is significantly higher while its computational cost is much lower.

Although specialized features have achieved excellent results in detecting fault conditions, they got mediocre results to identify the type of fault. This problem has been overcome using generic features that have shown a remarkable performance in discriminating the causes of faulty conditions.

Generic features have also shown a more robust behavior than raw or specialized features in synthetic datasets where the original design matrices were corrupted by an increasing level of random noise.

On the other hand, the size of the dataset required for classifiers using generic features is remarkable smaller than those needed for specialized or, even more, for raw features. The size of the dataset available for this research (about 40 minutes of vibration signals) has revealed to be enough for the two first cases, but insufficient for the raw features case.

The research has also revealed that, splitting the original vibration signals in smaller segments, increases the number of training examples, which can help to achieve a better classification accuracy. An optimal segment length has been deduced, as too short segments do not properly represent their health states and too large ones yield few training instances.

To enhance the applicability of our method, future studies could explore extending this approach to other types of machinery commonly used in the agri-food industry, such as conveyors, mixers, or pumps. These machines also generate vibration signals, and a similar classification framework could potentially improve maintenance practices across diverse equipment types.

To further improve dataset size, a logical next step would be to conduct data collection campaigns across multiple facilities and under varied operational conditions. This would enable a more comprehensive dataset that captures a wider range of potential equipment states and wear patterns. Additionally, integrating advanced signal processing techniques, such as wavelet transforms or cepstral analysis, could help extend generic feature extraction to other domains, improving the method’s robustness and accuracy.

These steps could contribute to a more generalized, scalable AI-driven solution for equipment health monitoring in the agri-food sector.