Skip to main content

Advertisement

Springer Nature Link
Log in

Integrating planning and control for single-bodied wheeled mobile robots

  • Published:
Autonomous Robots Aims and scope Submit manuscript

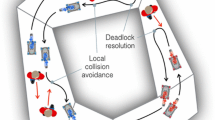
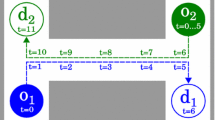
Abstract

This paper presents an approach to couple path planning and control for mobile robot navigation in a hybrid control framework. We build upon an existing hybrid control approach called sequential composition, in which a set of feedback control policies are prescribed on well-defined domains contained in the robot’s free space. Each control policy drives the robot to a goal set, which lies in the domain of a subsequent policy. Control policies are deployed into the free state space so that when composed among one another, the overall action of the set of control policies drives the robot to perform a task, such as moving from a start to a goal location or patrolling a perimeter. A planner determines the sequence of control policies to be invoked. When control policies defined in this framework respect the low-level dynamics and kinematics of the system, this formal approach guarantees that high-level tasks are either accomplished by a given set of policies, or verifies that the tasks are not achievable with the given policies.

Specifically, this paper makes three key contributions to the technique of sequential composition. First, we allow for a larger variety of transitions among the control policies, which results in a richer set of generated behaviors. In particular, we are able to design policies that respect multiple interacting constraints including obstacles, nonholonomic constraints, and input bounds. This is achieved by utilizing flow-through control policies, which allow the robot to exit the policy domain through a subset of the domain boundary. Second, our hybrid control approach lifts the planning problem from working in trajectory space to control policy space, allowing for both more efficient and meaningful symbolic planners to be employed for systems with nonholonomic constraints. Finally, we address the issue of deploying control policies in configuration spaces whose obstacles have curvature (i.e., are not polytopes in configuration space); ultimately, such an approach results in the collection of policy domains only approximating the free space. We believe this trade-off is necessary, and provide a technique to measure the relative completeness of the approximation. The paper concludes with an experimental validation of our approach on a mobile robot.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Balluchi, A., Bicchi, A., Balestrino, A., & Casalino, G. (1996). Path tracking control for Dubin’s car. In IEEE International conference on robotics and automation (pp. 3123–3128), Minneapolis, MN.

    Google Scholar 

  • Belta, C., Iser, V., & Pappas, G. J. (2005). Discrete abstractions for robot planning and control in polygonal environments. IEEE Transactions on Robotics, 21(5), 864–874.

    Article  Google Scholar 

  • Bloch, A. M., Baillieul, J., Crouch, P., & Marsden, J. (2003). Nonholonomic mechanics and control. Berlin: Springer.

    Book  MATH  Google Scholar 

  • Boyd, S., & Vandenberghe, L. (2004). Convex optimization. Cambridge: Cambridge University Press.

    MATH  Google Scholar 

  • Branicky, M. S. (1999). Behavioral programming. In Working notes AAAI spring symp. on hybrid systems and AI, Stanford, CA.

    Google Scholar 

  • Brock, O., & Kavraki, L. E. (2001). Decomposition-based motion planning: a framework for real-time motion planning in high-dimensional configuration places. In Proceedings of IEEE international conference on robotics and automation (pp. 1469–1475).

    Google Scholar 

  • Brockett, R. (1983). Asymptotic stability and feedback stabilization. In R. W. Brockett, R. S. Millman, & H. J. Sussmann (Eds.), Differential geometric control theory (pp. 181–191). Cambridge: Birkhauser Boston.

    Google Scholar 

  • Brockett, R. (1988). On the computer control of movement. In Proceedings of the 1988 IEEE international conference on robotics and automation (Vol. 1, pp. 534–540).

    Chapter  Google Scholar 

  • Burridge, R. R., Rizzi, A. A., & Koditschek, D. E. (1999). Sequential composition of dynamically dexterous robot behaviors. International Journal of Robotics Research, 18(6), 534–555.

    Article  Google Scholar 

  • Clarke, E. M., & Peled, O. G. D. (1999). Model checking. Cambridge: MIT Press.

    Google Scholar 

  • Conner, D. C. (2008). Integrating planning and control for constrained dynamical systems. Ph.D. Thesis: CMU-RI-TR-08-01 (available at http://www.ri.cmu.edu/pubs/pub_5961.html), Robotics Institute, Carnegie Mellon University, Pittsburgh, PA.

  • Conner, D. C., Rizzi, A. A., & Choset, H. (2003). Composition of local potential functions for global robot control and navigation. In IEEE/RSJ int’l. conf. on intelligent robots and systems (pp. 3546–3551), Las Vegas, NV.

    Google Scholar 

  • Conner, D. C., Choset, H., & Rizzi, A. A. (2006). Integrated planning and control for convex-bodied nonholonomic systems using local feedback control policies. In Proceedings of robotics: science and systems II, Philadelphia, PA.

    Google Scholar 

  • Conner, D. C., Kress-Gazit, H., Choset, H., Rizzi, A. A., & Pappas, G. J. (2007). Valet parking without a valet. In 2007 IEEE/RSJ international conference on intelligent robots and systems (pp. 572–577).

    Chapter  Google Scholar 

  • Conner, D. C., Choset, H., & Rizzi, A. A. (2009). Flow-through policies for hybrid controller synthesis applied to fully actuated systems. IEEE Transactions on Robotics, 25(1), 136–146.

    Article  Google Scholar 

  • DeCarlo, R., Zak, S., & Matthews, G. (1988). Variable structure control of nonlinear multivariable systems: a tutorial. Proceedings of the IEEE 76(3).

  • DeCarlo, R., Branicky, M., Pettersson, S., & Lennartson, B. (2000). Perspectives and results on the stability and stabilizability of hybrid systems. Proceedings of the IEEE, Special Issue on Hybrid Systems, 88(7), 1069–1082.

    Google Scholar 

  • Egerstedt, M., & Brockett, R. (2003). Feedback can reduce the specification complexity of motor programs. IEEE Transactions on Automatic Control, 48(2), 213–223.

    Article  MathSciNet  Google Scholar 

  • Fainekos, G., Kress-Gazit, H., & Pappas, G. J. (2005a). Hybrid controllers for path planning: a temporal logic approach. In IEEE conference on decision and control, Seville, Spain.

    Google Scholar 

  • Fainekos, G., Kress-Gazit, H., & Pappas, G. J. (2005b). Temporal logic planning for mobile robots. In IEEE conference on robotics and automation, Barcelona, Spain.

    Google Scholar 

  • Frazzoli, E., Dahleh, M., & Feron, E. (2005). Maneuver-based motion planning for nonlinear systems with symmetries. IEEE Transactions on Robotics, 21(6), 1077–1091.

    Article  Google Scholar 

  • Habets, L. C. G. J. M., & van Schuppen, J. H. (2001). Control of piecewise-linear hybrid systems on simplices and rectangles. In Lecture notes in computer science: Vol. 2034. Hybrid systems: computation and control (pp. 261–274).

    Chapter  Google Scholar 

  • Habets, L. C. G. J. M., Collins, P. J., & van Schuppen, J. H. (2006). Reachability and control synthesis for piecewise-affine hybrid systems on simplices. IEEE Transactions on Automatic Control, 51(6), 938–948.

    Article  Google Scholar 

  • Hammersley, J. M., & Handscomb, D. C. (1964). Monte Carlo methods. London: Chapman and Hall.

    MATH  Google Scholar 

  • Hristu-Varsakelis, D., Egerstedt, M., & Krishnaprasad, P. (2003). On the structural complexity of the motion description language MDLe. In Proceedings of 42nd IEEE conference on decision and control (Vol. 4, pp. 3360–3365).

    Google Scholar 

  • Kantor, G., & Rizzi, A. A. (2003a). Feedback control of underactuated systems via sequential composition: visually guided control of a unicycle. In Proceedings of 11th international symposium of robotics research.

    Google Scholar 

  • Kantor, G. A., & Rizzi, A. A. (2003b). Sequential composition for control of underactuated systems (Technical Report TR-03-23). Robotics Institute, Carnegie Mellon University, Pittsburgh, PA.

  • Kloetzer, M., & Belta, C. (2006). A fully automated framework for control of linear systems from LTL specifications. In 9th international workshop on hybrid systems: computation and control, Santa Barbara, California.

    Google Scholar 

  • Kloetzer, M., & Belta, C. (2007). Managing non-determinism in symbolic robot motion planning and control. In IEEE international conference on robotics and automation (ICRA), Rome, Italy.

    Google Scholar 

  • Kress-Gazit, H., Fainekos, G. E., & Pappas, G. J. (2007). Where’s Waldo? Sensor-based temporal logic motion planning. In IEEE international conference on robotics and automation (pp. 3116–3121), Rome, Italy.

    Google Scholar 

  • Kress-Gazit, H., Conner, D. C., Choset, H., Rizzi, A. A., & Pappas, G. J. (2008). Courteous cars: decentralized multiagent traffic coordination. IEEE Robotics and Automation Magazine.

  • Liberzon, D., & Morse, A. S. (1999). Basic problems in stability and design of switched systems. IEEE Control Systems, 59–70.

  • Likhachev, M., & Koenig, S. (2003). Speeding up the parti-game algorithm. In Advances in neural information processing systems, (Vol. 15). Cambridge: MIT Press.

    Google Scholar 

  • Lindemann, S. R., & LaValle, S. M. (2005). Smoothly blending vector fields for global robot navigation. In IEEE conference on decision and control (pp. 3553–3559), Seville, Spain.

    Google Scholar 

  • Lindemann, S. R., & LaValle, S. M. (2007). Smooth feedback for car-like vehicles in polygonal environments. In IEEE international conference on robotics and automation (ICRA) (pp. 3104–3109), Rome, Italy.

    Google Scholar 

  • Lindemann, S. R., Hussein, I. I., & LaValle, S. M. (2006). Realtime feedback control for nonholonomic mobile robots with obstacles. In IEEE conference on decision and control (pp. 2406–2411), San Diego, CA.

    Google Scholar 

  • Manikonda, V., Krishnaprasad, P., & Hendler, J. (1998). Languages, behaviors, hybrid architectures and motion control.

  • Nelson, W. L. (1989). Continuous curvature paths for autonomous vehicles. In IEEE international conference on robotics and automation (Vol. 3, pp. 1260–1264), Scottsdale, AZ.

    Google Scholar 

  • Patel, S., Jung, S.-H., Ostrowski, J. P., Rao, R., & Taylor, C. J. (2002). Sensor based door navigation for a nonholonomic vehicle. In IEEE international conference on robotics and automation (pp. 3081–3086), Washington, DC.

    Google Scholar 

  • Pathak, K., & Agrawal, S. K. (2005). An integrated path-planning and control approach for nonholonomic unicycles using switched local potentials. IEEE Transactions on Robotics, 21(6), 1201–1208.

    Article  Google Scholar 

  • Rizzi, A. A. (1998). Hybrid control as a method for robot motion programming. In IEEE international conference on robotics and automation (Vol. 1, pp. 832–837).

    Google Scholar 

  • Roszak, B., & Broucke, M. E. (2006). Necessary and sufficient conditions for reachability on a simplex. Automatica, 42(11), 1913–1918.

    Article  MathSciNet  MATH  Google Scholar 

  • Yang, L., & Lavalle, S. M. (2004). The sampling-based neighborhood graph: an approach to computing and executing feedback motion strategies. IEEE Transactions on Robotics and Automation, 20(3), 419–432.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, 15213, USA

    David C. Conner & Howie Choset

  2. Boston Dynamics, Waltham, MA, 02451, USA

    Alfred A. Rizzi

Authors
  1. David C. Conner
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Howie Choset
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Alfred A. Rizzi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Howie Choset.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Conner, D.C., Choset, H. & Rizzi, A.A. Integrating planning and control for single-bodied wheeled mobile robots. Auton Robot 30, 243–264 (2011). https://doi.org/10.1007/s10514-011-9217-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10514-011-9217-4

Keywords