Abstract
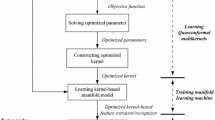
The aim of this paper is to solve the problem of unsupervised manifold regularization being used under supervised classification circumstance. This paper not only considers that the manifold information of data can provide useful information but also proposes a supervised method to compute the Laplacian graph by using the label information and the Hellinger distance for a comprehensive evaluation of the similarity of data samples. Meanwhile, multi-source or complex data is increasing nowadays. It is desirable to learn from several kernels that are adaptable and flexible to deal with this type of data. Therefore, our classifier is based on multiple kernel learning, and the proposed approach to supervised classification is a multiple kernel model with manifold regularization to incorporate intrinsic geometrical information. Finally, a classifier that minimizes the testing error and considers the geometrical structure of data is put forward. The results of experiments with other methods show the effectiveness of the proposed model and computing the inner potential geometrical information is useful for classification.

Similar content being viewed by others
References
Murty, M.N., Devi, V.S.: Introduction to pattern recognition and machine learning. J. Cell. Physiol. 200(1), 71–81 (2015)
Hinton, G.E., Osindero, S., Teh, Y.W.: A fast learning algorithm for deep belief nets. Neural Comput. 18(7), 1527–1554 (2014)
Sheu, J., Chen, Y., Chu, K., et al.: An intelligent three-phase spam filtering method based on decision tree data mining. Secur. Commun. Netw. 9(17), 4013–4026 (2016)
Campello, B., Moulavi, D., Zimek, A., Sander, J.: A framework for semisupervised and unsupervised optimal extraction of clusters from hierarchies. Data Min. Knowl. Discov. 27(3), 344–371 (2013)
Sørensen, A.P.W.: Geometric classification of simple graph algebras. Ergod. Theory Dyn. Syst. 33(4), 1199–1220 (2013)
Criminisi, A., Shotton, J.: Semi-supervised classification forests. Adv. Comput. Vis. Pattern Recognit. 161, 544–563 (2013)
Wang, B., Tu, Z., Tsotsos, J.K.: Dynamic label propagation for semi-supervised multi-class multi-label classification. Pattern Recognit. 52, 75–85 (2016)
Belkin, M., Niyogi, P., Sindhwani, V.: Manifold regularization: a geometric framework for learning from labels and unlabels examples. J. Mach. Learn. Res. 7(1), 2399–2434 (2006)
Xing, X., Yu, Y., Jiang, H., et al.: A multi-manifold semi-supervised Gaussian mixture model for pattern classification. Pattern Recognit. Lett. 34(16), 2118–2125 (2013)
Lanckriet, G., Cristianini, N., Bartlett, P., Ghaoui, L.E., Jordan, M.: Learning the kernel matrix with sem-idefinite programming. J. Mach. Learn. Res. 5(1), 323–330 (2004)
Liang, Z., Zhang, L., Liu, J.: A novel multiple kernel learning method based on the Kullback-Leibler divergence. Neural Process. Lett. 42(3), 1–18 (2015)
Bucak, S., Jin, R., Jain, A.K.: Multiple kernel learning for visual object recognition: a review. IEEE Trans. Pattern Anal. Mach. Intell. 36(7), 1354–1369 (2014)
Rakotomamonjy, A., Bach, F., Canu, S., Grandvalet, Y.: SimpleMKL. J. Mach. Learn. Res. 9(3), 2491–2521 (2008)
Althloothi, S., Mahoor, M.H., Zhang, X.: Human activity recognition using multi-features and multiple ker-nel learning. Pattern Recognit. 47(5), 1800–1812 (2014)
Nazarpour, A., Adibi, P.: Two-stage multiple kernel learning for supervised dimensionality reduction. Pattern Recognit. 48(5), 1854–1862 (2015)
Aiolli, F., Donini, M.: EasyMKL: a scalable multiple kernel learning algorithm. Neurocomputing 169, 215–224 (2015)
Yang, T., Fu, D.: Semi-supervised classification with Laplacian multiple kernel learning. Neurocomputing 140, 19–26 (2014)
Cao, Y., Chen, D.R.: Generalization errors of Laplacian regularized least squares regression. Sci. China Math. 55(9), 1859–1868 (2012)
Arqub, O.A., Al-Smadi, M., Momani, S., et al.: Numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method. Soft. Comput. 20(8), 3283–3302 (2016)
Mcfee, B., Lanckriet, G.: Learning multi-modal similarity. J. Mach. Learn. Res. 12(8), 491–523 (2010)
Dinuzzo, F., Neve, M., Necolao, G.D.: On the representer theorem and equivalent degrees of freedom of SVR. J. Mach. Learn. Res. 8(8), 2467–2495 (2007)
Ladd, A.M., Kavraki, L.E.: Measure theoretic analysis of probabilistic path planning. IEEE Trans. Robot. Autom. 20(2), 229–242 (2004)
Chrétien, B., Escande, A., Kheddar, A.: GPU robot motion planning using semi-infinite nonlinear programming. IEEE Trans. Parallel Distrib. Syst. 27(10), 1–1 (2016)
Micchelli, C.A., Pontil, M., Wu, Q., et al.: Error bounds for learning the kernel. Anal. Appl. 14(06), 849–868 (2016)
Ying, Y., Campbell, C.: Rademacher chaos complexities for learning the kernel problem. Neural Comput. 22(11), 2858–2886 (2014)
Ashok, P., Nawaz, G.M.K.: Outlier detection method on UCI repository dataset by entropy based rough K-means. Def. Sci. J. 66(2), 113–119 (2016)
Johnson, D., Xiong, C., Corso, J.: Semi-supervised nonlinear distance metric learning via forests of max-margin cluster hierarchies. IEEE Trans. Knowl. Data Eng. 28(4), 1035–1046 (2016)
Chang, C.C., Lin, C.J.: LIBSVM: a library for support vector machines. Trans. Intell. Syst. Technol. 2, 27–27 (2011)
Ding, G., Wu, Q., Yao, Y.D., et al.: Kernel-based learning for statistical signal processing in cognitive radio networks: theoretical foundations, example applications, and future directions. IEEE Signal Process. Mag. 30(4), 126–136 (2013)
Harchaoui, Z., Bach, F., Cappe, O., et al.: Kernel-based methods for hypothesis testing: a unified view. IEEE Signal Process. Mag. 30(4), 87–97 (2013)
Bazerque, J.A., Giannakis, G.B.: Nonparametric basis pursuit via sparse kernel-based learning: a unifying view with advances in blind methods. IEEE Signal Process. Mag. 30(4), 112–125 (2013)
Acknowledgements
The authors acknowledge the China Postdoctoral Science Foundation (No. 2017M620615) and Fundamental Research Funds for the Central Universities (Grant: FRF-TP-16-082A1) and National Natural Science Foundation of China (No. 61272358).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Yang, T., Fu, D., Li, X. et al. Manifold regularized multiple kernel learning with Hellinger distance. Cluster Comput 22 (Suppl 6), 13843–13851 (2019). https://doi.org/10.1007/s10586-018-2106-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10586-018-2106-2