Abstract
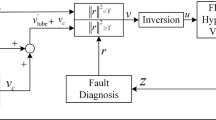
In this paper, the linear parameter varying (LPV) reliable non-fragile control for the hypersonic vehicle (HV) is studied in case of disturbance and controller gain variations. Due to the dramatic and complex change of the HV longitudinal dynamics, a polytopic LPV model is constructed for the HV system stability analysis and controller design in a large flight envelope. Then, a disturbance observer (DOB)-based non-fragile controller for HV system with disturbance and unknown controller uncertainty is designed to guarantee the closed-loop stability and control performance under an adequate level of reliability, which is formed with two parts. One part is a DOB to compensate the uncertain dynamics and disturbance. The other is a robust non-fragile controller, which is designed based on a novel robust reliability method to deal with controller uncertainties, and obtained by carrying out reliability-based linear matrix inequality optimization. The presented controller for HV can provide the robustness as well as an excellent performance under the condition that the prescribed reliability degree is satisfied. Finally, numerical simulation for an HV demonstrates the effectiveness of the proposed method.









Similar content being viewed by others
References
Xu, B., Shi, Z.: An overview on flight dynamics and control approaches for hypersonic vehicles. Sci. China Inform. Sci. 58(7), 1–19 (2015)
Marrison, C.I., Stengel, R.F.: Design of robust control systems for a hypersonic aircraft. J. Guid. Control Dyn. 21(1), 58–63 (1998)
Huang, J., Tu, X., He, J.: Design and evaluation of the RUPERT wearable upper extremity exoskeleton robot for clinical and in-home therapies. IEEE Trans. Syst. Man Cybern. Syst. 46(7), 926–935 (2016)
Bolender, M.A., Doman, D.B.: Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle. J. Spacecr. Rockets 44(2), 374–387 (2007)
Parker, J.T., Serrani, A., Yurkovich, S., Bolender, M.A., Doman, D.B.: Control-oriented modeling of an air-breathing hypersonic vehicle. J. Guid. Control Dyn. 30(3), 856–869 (2007)
Buschek, H., Calise, A.J.: Uncertainty modeling and fixed-order controller design for a hypersonic vehicle model. J. Guid. Control Dyn. 20(1), 42–48 (1997)
Li, H., Si, Y., Wu, L., Hu, X., Gao, H.: Guaranteed cost control with poles assignment for a flexible air-breathing hypersonic vehicle. Int. J. Syst. Sci. 42(5), 863–876 (2011)
Sigthorsson, D., Jankovsky, P., Serrani, A., Yurkovich, S., Bolender, M., Doman, D.B.: Robust linear output feedback control of an airbreathing hypersonic vehicle. J. Guid. Control Dyn. 31(4), 1052–1066 (2008)
An, H., Wang, C., Fidan, B.: Sliding mode disturbance observer-enhanced adaptive control for the air-breathing hypersonic flight vehicle. Acta Astronaut. 139, 111–121 (2017)
Xu, B.: Robust adaptive neural control of flexible hypersonic flight vehicle with dead-zone input nonlinearity. Nonlinear Dyn. 80(3), 1509–1520 (2015)
Zong, Q., Ji, Y., Zeng, F., Liu, H.: Output feedback back-stepping control for a generic hypersonic vehicle via small-gain theorem. Aerosp. Sci. Technol. 23(1), 409–417 (2012)
Xu, B., Yang, C., Pan, Y.: Global neural dynamic surface tracking control of strict-feedback systems with application to hypersonic flight vehicle. IEEE Trans. Neural Netw. Learn. 26(10), 2563–2575 (2015)
Yan, X.-G., Spurgeon, S.K., Zhu, Q., Zhang, Q.: Memoryless variable structure control for affine nonlinear systems using only output information. Int. J. Robust Nonlinear 25(17), 3316–3329 (2015)
Mu, C., Ni, Z., Sun, C., He, H.: Air-breathing hypersonic vehicle tracking control based on adaptive dynamic programming. IEEE Trans. Neural Netw. Learn. 28(3), 584–598 (2017)
Ye, J., Ding, Y.: Controllable keyword search scheme supporting multiple users. Future Gener. Comput. Syst. 81, 433–442 (2018)
Huang, J., Wang, Y., Fukuda, T.: Set-membership-based fault detection and isolation for robotic assembly of electrical connectors. IEEE Trans. Autom. Sci. Eng. 15(1), 160–171 (2018)
Cai, G.B., Duan, G.R., Hu, C.H.: A velocity-based LPV modeling and control framework for an airbreathing hypersonic vehicle. Int. J. Innov. Comput. I 7(5A), 2269–2281 (2011)
Lind, R.: Linear parameter-varying modeling and control of structural dynamics with aerothermoelastic effects. J. Guid. Control Dyn. 25(4), 733–739 (2002)
Wu, L., Yang, X., Li, F.: Nonfragile output tracking control of hypersonic air-breathing vehicles with an LPV model. IEEE-ASME Trans. Mechatron. 18(4), 1280–1288 (2013)
Baranyi, P.: TP model transformation as a way to LMI-based controller design. IEEE Trans. Ind. Electron. 51(2), 387–400 (2004)
Cheng, H., Dong, C., Jiang, W., Wang, Q., Hou, Y.: Non-fragile switched H∞ control for morphing aircraft with asynchronous switching. Chin. J. Aeronaut. 30(3), 1127–1139 (2017)
Guo, L., Chen, W.-H.: Disturbance attenuation and rejection for systems with nonlinearity via DOBC approach. Int. J. Robust Nonlinear 15(3), 109–125 (2005)
Wu, G., Meng, X.: Nonlinear disturbance observer based robust backstepping control for a flexible air-breathing hypersonic vehicle. Aerosp. Sci. Technol. 54, 174–182 (2016)
Xu, B., Shi, Z., Yang, C.: Composite fuzzy control of a class of uncertain nonlinear systems with disturbance observer. Nonlinear Dyn. 80(1), 341–351 (2015)
Xu, B., Sun, F., Pan, Y., Chen, B.: Disturbance observer based composite learning fuzzy control of nonlinear systems with unknown dead zone. IEEE Trans. Syst. Man Cybern. Syst 47(8), 1854–1862 (2017)
Wu, H.-N., Feng, S., Liu, Z.-Y., Guo, L.: Disturbance observer based robust mixed H2/H∞ fuzzy tracking control for hypersonic vehicles. Fuzzy Set. Syst. 306, 118–136 (2017)
Huang, J., Ri, S., Liu, L., Wang, Y., Kim, J., Pak, G.: Nonlinear disturbance observer-based dynamic surface control of mobile wheeled inverted pendulum. IEEE Trans. Control Syst. Technol. 23(6), 2400–2407 (2015)
Huang, Y., Sun, C., Qian, C., Wang, L.: Non-fragile switching tracking control for a flexible air-breathing hypersonic vehicle based on polytopic LPV model. Chin. J. Aeronaut. 26(4), 948–959 (2013)
Wu, H., Lian, J., Wu, J., Wang, Y.: Research on non-fragile robust control of high-speed reentry vehicle. In: 21st AIAA International Space Planes and Hypersonics Technologies Conference, Xiamen, China, 6–9 Mar 2017
Liu, C., Sun, Z., Shi, K., Wang, F.: Robust dynamic output feedback control for attitude stabilization of spacecraft with nonlinear perturbations. Aerosp. Sci. Technol. 64, 102–121 (2017)
Guo, S.-X.: Non-probabilistic robust reliability method and reliability-based performance optimization for active vibration control of structures and dynamic systems with bounded uncertain parameters. J. Vib. Control 22(6), 1472–1491 (2016)
Guo, S.-X.: Robust reliability method for non-fragile guaranteed cost control of parametric uncertain systems. Syst. Control Lett. 64, 27–35 (2014)
Ditlevsen, O.D., Madsen, H.O.: Structural Reliability Methods, 2nd edn. John Wiley & Sons Inc, New York (2007)
Guo, S.-X.: Robust reliability as a measure of stability of controlled dynamic systems with bounded uncertain parameters. J. Vib. Control 16(9), 1351–1368 (2010)
Tanaka, K., Wang, H.O.: Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach. John Wiley & Sons Inc, New York (2002)
Tuan, H.D., Apkarian, P., Narikiyo, T., Yamamoto, Y.: Parameterized linear matrix inequality techniques in fuzzy control system design. IEEE Trans. Fuzzy Syst. 9(2), 324–332 (2001)
Hu, X., Wu, L., Hu, C., Gao, H.: Fuzzy guaranteed cost tracking control for a flexible air-breathing hypersonic vehicle. IET Control Theory Appl. 6(9), 1238 (2012)
Yam, Y., Baranyi, P., Yang, C.T.: Reduction of fuzzy rule base via singular value decomposition. IEEE Trans. Fuzzy Syst. 7(2), 120–132 (1999)
Petersen, I.R.: A stabilization algorithm for a class of uncertain linear systems. Syst. Control Lett. 8(4), 351–357 (1987)
Acknowledgements
This work was supported in part by the National Nature Science Foundation of China (Grant Nos. 61473124 and 61573161).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The author(s) declare no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Appendices
Appendix 1
where
Appendix 2
Proof of Theorem 1
For \(Q = Q^{T} \ge 0\) and \(R = R^{T} \ge 0\), it can be seen from (26) that
For the control system (22), the Lyapunov function can be selected as follows
then take the time derivative of \(V(\tilde{x})\), and we obtain
According to Lemma 1 [39], we have
then
from this and Eq. (68), we have \(\dot{V}(\tilde{x}) < 0\). Therefore, on the basis of the Lyapunov stability theory, the control system (22) is asymptotically stable with \(y_{r} (t) = 0\).Then, we consider the performance index \(J\) in (25)
The proof is completed.□
Rights and permissions
About this article
Cite this article
Wei, X., Liu, L. & Wang, Y. Reliability-based linear parameter varying robust non-fragile control for hypersonic vehicles with disturbance observer. Cluster Comput 22 (Suppl 3), 6709–6728 (2019). https://doi.org/10.1007/s10586-018-2528-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10586-018-2528-x