Abstract
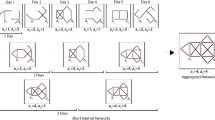
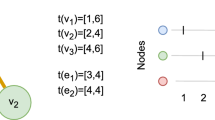
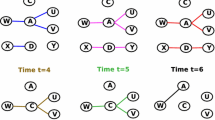
Longitudinal networks evolve over time through the creation and/or deletion of links among a set of actors (e.g., individuals or organizations). A longitudinal network can be viewed as a single static network (i.e., structure of network is fixed) that aggregates all the edges observed over some time period or as a series of static networks observed in different point of time over the entire network observation period (i.e., structure of network is changing over time). The understanding of the underlying structural changes of longitudinal networks and contributions of individual actors to these changes enable researchers to investigate different structural properties of such networks. By following a topological approach (i.e., static topology and dynamic topology), this paper first proposes a framework to analyze longitudinal social networks. In static topology, social networks analysis (SNA) methods are applied to the aggregated network of entire observation period. Smaller segments of network data (i.e., short-interval network) that are accumulated in less time compared to the entire network observation period are used in the dynamic topology for analysis purposes. Based on this framework, this study then conducts topological analysis of two longitudinal networks to explore over time actor-level dynamics during different phases of these two networks. The proposed topological framework can be utilized to explore structural vulnerabilities and evolutionary trend of various longitudinal social networks (e.g., disease spread network and computer virus network). This will eventually lead to better authorization and control over such networks. For network science researchers, this framework will bring new research opportunities to enhance our present knowledge about different aspects (e.g., network disintegration and contribution of individual actor’s to network evolution) of longitudinal social networks.



Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Banks DL, Carley KM (1996) Models for network evolution. J Math Sociol 21(1–2):173–196
Bickart KC, Wright CI, Dautoff RJ, Dickerson BC, Barrett LF (2010) Amygdala volume and social network size in humans. Nat Neurosci 14(2):163–164
Carley KM, Reminga J, and Kamneva N (1998) Destabilizing terrorist networks. Institute for Software Research, Pittsburgh, p. 45
Carley KM, Dombroski M, Tsvetovat M, Reminga J, Kamneva N (2003) Destabilizing dynamic covert networks. International Command and Control Research and Technology Symposium, National Defense War College, Wasington DC
Coffee JC Jr (2001) Understanding Enron: it’s about the gatekeepers, stupid. Bus Law 57:1403
Dabholkar PA, Shepherd CD, Thorpe DI (2000) A comprehensive framework for service quality: an investigation of critical conceptual and measurement issues through a longitudinal study. J Retail 76(2):139–173
Diggle P (2002) Analysis of longitudinal data. Oxford University Press, USA
Drutman L, Hopkins DJ (2013) The inside view: using the Enron e-mail archive to understand corporate political attention. Legis Stud Q 38(1):5–30
Feld SL (1997) Structural embeddedness and stability of interpersonal relations. Soc Netw 19(1):91–95
Hill SA, Braha D (2010) Dynamic model of time-dependent complex networks. Phys Rev E 82(4):046105
Holland PW, Leinhardt S (1977) A dynamic model for social networks. J Math Sociol 5(1):5–20
Kim H, Anderson R (2012) Temporal node centrality in complex networks. Phys Rev E 85(2):026107
Masuda N, Ohtsuki H (2009) Evolutionary dynamics and fixation probabilities in directed networks. New J Phys 11:033012
Mercken L, Steglich C, Sinclair P, Holliday J, Moore L (2012) A longitudinal social network analysis of peer influence, peer selection, and smoking behavior among adolescents in British schools. Health Psychol 31(4):450–459
Mogus AM, Djurdjevic I, Suvak N (2012) The impact of student activity in a virtual learning environment on their final mark. Act Learn High Educ 13(3):177–189
Newcomb TM (1961) The acquaintance process. Holt, Rinehart and Winston, New York
Novak M, Wootton JT, Doak DF, Emmerson M, Estes JA, Tinker MT (2011) Predicting community responses to perturbations in the face of imperfect knowledge and network complexity. Ecology 92(4):836–846
Pattison P, Wasserman S, Robins G, Kanfer AM (2000) Statistical evaluation of algebraic constraints for social networks. J Math Psychol 44(4):536–568
Pfeffer J, Carley KM (2012) k-Centralities: local approximations of global measures based on shortest paths. Proceedings of the 21st international conference companion on World Wide Web, ACM
Roberts J, Armitage J (2006) From organization to hypermodern organization: on the accelerated appearance and disappearance of Enron. J Organ Change Manag 19(5):558–577
Robins G, Pattison P (2001) Random graph models for temporal processes in social networks*. J Math Sociol 25(1):5–41
Robins G, Pattison P (2005) Interdependencies and social processes: dependence graphs and generalized dependence structures. Models Methods Soc Netw Anal 28:192–214
Robins G, Pattison P, Wasserman S (1999) Logit models and logistic regressions for social networks: III. Valued relations. Psychometrika 64(3):371–394
Robins G, Pattison P, Kalish Y, Lusher D (2007) An introduction to exponential random graph (p*) models for social networks. Soc Netw 29(2):173–191
Salathé M, Kazandjieva M, Lee JW, Levis P, Feldman MW, Jones JH (2010) A high-resolution human contact network for infectious disease transmission. Proc Natl Acad Sci 107(51):22020–22025
Sampson SF (1968) A novitiate in a period of change: an experimental and case study of social relationships. Unpublished doctoral dissertation, Cornell University
Sanil A, Banks D, Carley K (1995) Models for evolving fixed node networks: model fitting and model testing. Soc Netw 17(1):65–81
Snijders TAB (2005) Models for longitudinal network data. Cambridge University Press, New York
Snijders T, Van Duijn M (1997) Simulation for statistical inference in dynamic network models. Lect Notes Econ Math Syst 456:493–512
Snijders TA, Pattison PE, Robins GL, Handcock MS (2006) New specifications for exponential random graph models. Soc Methodol 36(1):99
Snijders TAB, Van de Bunt GG, Steglich CEG (2010) Introduction to stochastic actor-based models for network dynamics. Soc Netw 32(1):44–60
Uddin S, Jacobson MJ (2013) Dynamics of email communications among university students throughout a semester. Comput Educ 64:95–103
Uddin S, Hossain L, Murshed ST, Crawford JW (2011a) Static versus dynamic topology of complex communications network during organizational crisis. Complexity 16(5):27–36
Uddin S, Murshed STH, Hossain L (2011b) Power-law behaviour in complex organizational communication network during crisis. Phys A 390(15):2845–2853
Uddin S, Chung KSK and Piraveenan M (2012) Capturing actor-level dynamics of longitudinal networks. Advances in Social Networks Analysis and Mining (ASONAM), IEEE/ACM
Uddin S, Piraveenan M, Chung K and Hossain L (2013) Topological analysis of longitudinal networks. Hawaii international conference on system sciences (HICSS), Hawaii, USA, IEEE Computer Society
Van de Bunt GG, Van Duijn MAJ, Snijders TAB (1999) Friendship networks through time: an actor-oriented dynamic statistical network model. Comput Math Organ Theory 5(2):167–192
Wasserman S, Faust K (2003) Social network analysis: methods and applications. Cambridge University Press, Cambridge
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Uddin, S., Khan, A., Hossain, L. et al. A topological framework to explore longitudinal social networks. Comput Math Organ Theory 21, 48–68 (2015). https://doi.org/10.1007/s10588-014-9176-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10588-014-9176-3