Skip to main content
Springer Nature Link
Log in

A computational consumer-driven market model: statistical properties and the underlying industry dynamics

  • Manuscript
  • Published:
Computational and Mathematical Organization Theory Aims and scope Submit manuscript

Abstract

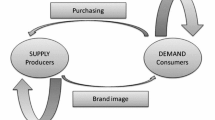
We present an agent-based market model in which social emulation by consumers and the adaptation of producers to demand play a significant role. Our theoretical approach considers boundedly-rational agents, heterogeneity of agents and product characteristics, and the co-evolution of consumers’ desires and firms’ adaptation efforts. The model reproduces, and allows us to interpret, statistical regularities which have been observed in the evolution of industrial sectors, and that seem to be also significant in the case of discretionary consumption activities. Thus, we suggest new determinants and explanations (from the consumer-side) for these stylized facts, and we obtain new theoretical patterns which may be of help to better understand the dynamics of discretionary goods markets. This model and results may contribute to guide future research on the field of consumer market.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Notes

  1. Those goods which are not strictly necessary for everyday life.

  2. Clearly these goods are heavily influenced by social emulation, and this could explain the emergence of consumer trends and the diversity of tastes.

  3. The characteristic space is inspired by Lancaster (1966).

  4. In each time period consumers only make one purchase decision but many social interactions can occur, which must take place sequentially in order to be implemented computationally. For this reason, periods are divided into steps and we use an asynchronous–random updating mechanism that sets the order in which consumers interact (see, for example, Miller and Page 2004).

  5. We consider the Euclidean distance, although depending on the specific features of each product, other metrics might be more suitable.

  6. We have considered that representative niches are those with a minimum size equivalent to 5 % of the population; clearly, other thresholds could be set up, but these changes produce no significant variations in the model dynamics.

  7. This parameter can measure two kinds of market opacity. On the demand side, the uncertainty regarding the precise desires of the niche. On the supply side, it shows the possibility of not being able to satisfy exactly the consumer desires, or not knowing how to do it technically.

  8. We are interested in proving that our model can show several well-known industrial patterns, which really requires finding only one specific parameter set that can generate them. In particular, in our simulations we take the default parameter values: N = 75, α = 24, β = 6, p = 0.003, r = 0.3, δ = 0.8, K = 0.1, M = 0.9, σ = 0.1, q = 0.05, λ = 0.003; although similar time evolutions of the system are obtained over a wide range of parameter values. All figures in this section have been obtained with these default parameter values and averaged from 500 replications (for different random seeds).

  9. Characterized by the three aggregate variables: level of adoption \({{\varLambda }}\left( t \right)\), number of producers \(\prod \left( t \right)\) and Herfindahl index H(t).

  10. We are only interested in proving the existence of a phase transition. The specific value of r that produces it, which depends on the values of the other parameters, is irrelevant for our purposes.

References

  • Addis M, Holbrook M (2001) On the conceptual link between mass customization and experimental consumption: an explosion of subjectivity. J Consum Behav 1:50–66

    Article  Google Scholar 

  • Agarwal S (2002) Restructuring seaside tourism. Ann Tour Res 29:25–55

    Article  Google Scholar 

  • Aversi R, Dosi G, Fagiolo G, Meacci M, Olivetti C (1999) Demand dynamics with socially evolving preferences. Ind Corp Change 8(2):353–408

    Article  Google Scholar 

  • Baudrillard J (1981) For a critique of the political economy of the signs. Telos Press, St. Louis

    Google Scholar 

  • Becker GS (1996) Accounting for tastes. Harvard University Press, Cambridge

    Google Scholar 

  • Bianchi M (ed) (1998) The active consumer. Routledge, London

    Google Scholar 

  • Bianchi M (2002) Novelty, preferences and fashion: when goods are unsettling. J Econ Behav Organ 47:1–18

    Article  Google Scholar 

  • Bottazzi G, Secchi A (2003) Common properties and sectoral specificities in the dynamics of US manufacturing companies. Rev Ind Organ 23(3–4):217–232

    Article  Google Scholar 

  • Bottazzi G, Cefis E, Dosi G, Secchi A (2003) Invariances and diversities in the evolution of manufacturing industries (No. 2003/21). LEM Working Paper Series

  • Butler RW (2011) Tourism area life cycle. Goodfellow Publishers, Oxford

    Google Scholar 

  • Camerer C, Loewenstein G, Prelec D (2005) Neuroeconomics: how neuroscience can inform economics. J Econ Lit 44:9–64

    Article  Google Scholar 

  • Cefis E (2003) Persistence in innovation and profitability. Rivista Internazionale di Scienze Sociali 110:19–37

    Google Scholar 

  • Chai A, Earl P, Potts J (2007) Fashion, growth and welfare: an evolutionary approach. Adv Austrian Econ 10:187–207

    Google Scholar 

  • Cowan R, Cowan W, Swann P (1997) A model of demand with interactions among consumers. Int J Ind Organ 15(6):711–732

    Article  Google Scholar 

  • De Vany A (2004) Hollywood economics. How extreme uncertainty shapes the film industry. Routledge, London

    Google Scholar 

  • Deci E, Flaste R (1996) Why we do what we do: understanding self-motivation. Penguins Books, New York

    Google Scholar 

  • Dosi G (2007) Statistical regularities in the evolution of industries. A guide through some evidence and challenges for the theory. In: Malerba F, Brusoni S (eds) Perspectives on innovation. Cambridge University Press, Cambridge, pp 153–186

    Chapter  Google Scholar 

  • Dosi G, Nelson RR (2010) Technical change and industrial dynamics as evolutionary processes. Hand Econ Innov 1:51–127

    Article  Google Scholar 

  • Evans DS (1987) Tests of alternative theories of firm growth. J Polit Econ 95:657–674

    Article  Google Scholar 

  • Fernández-Márquez CM, Vázquez FJ (2014) A simple emulation-based computational model. J Artif Soc Soc Simul 17(2):1–23

    Article  Google Scholar 

  • Fernández-Márquez CM, Fatás-Villafranca F, Vázquez FJ (2016) Endogenous demand and demanding consumers: a computational approach. Comput Econ (forthcoming)

  • Foxall GR (1990) Consumer psychology in behavioral perspective. Routledge, London

    Google Scholar 

  • Gilbert D, Abdullah J (2004) Holiday taking and the sense of well-being. Ann Tour Res 31:103–121

    Article  Google Scholar 

  • Hall BH, Rosenberg N (eds) (2010) Handbook of the economics of innovation, vol 2. Elsevier-North Holland, New York

    Google Scholar 

  • Hunt RWG (2004) The reproduction of colour. Wiley, Chichester

    Book  Google Scholar 

  • Jackson MO (2008) Social and economic networks. Princeton University Press, Oxford

    Google Scholar 

  • Klepper S (1997) Industry life cycles. Ind Corp Change 6(1):145–182

    Article  Google Scholar 

  • Lancaster KJ (1966) A new approach to consumer theory. J Polit Econ 74(2):132–157

    Article  Google Scholar 

  • Lebergott S (1993) Pursuing happiness. American consumers in the 20th Century. Princeton University Press, Princeton

    Google Scholar 

  • Leiss W (1983) The icons of the market place. Theory Cult Soc 1(3):10–21

    Article  Google Scholar 

  • Loasby B (2001) Cognition, imagination and institutions in demand creation. J Evolut Econ 11(1):7–21

    Article  Google Scholar 

  • Lotti F, Santarelli E, Vivarelli M (2003) Does Gibrat’s Law hold among young, small firms? J Evolut Econ 13(3):213–235

    Article  Google Scholar 

  • Malerba F, Nelson R, Orsenigo L, Winter S (2007) Demand, innovation, and the dynamics of market structure: the role of experimental users and diverse preferences. J Evolut Econ 17(4):371–399

    Article  Google Scholar 

  • Marsali M, Vega-Redondo F, Slanina F (2007) The rise and fall of a networked society: a formal model. Proc Natl Acad Sci USA 101:1439–1442

    Article  Google Scholar 

  • Miller JH, Page SE (2004) The standing ovation problem. Complexity 9(5):8–16

    Article  Google Scholar 

  • Moreau C, Lehmann D, Markman A (2001) Entrenched knowledge structure and consumer response to new products. J Mark Res 38:14–16

    Article  Google Scholar 

  • Mowery DC, Nelson RR (eds) (1999) Sources of industrial leadership: studies of seven industries. Cambridge University Press, Cambridge

    Google Scholar 

  • Nelson RR, Consoli D (2010) An evolutionary theory of household consumption behavior. J Evolut Econ 20(5):665–687

    Article  Google Scholar 

  • Nelson RR, Winter SG (1982) An evolutionary theory of economic change. Belknap Press, Cambridge

    Google Scholar 

  • North MJ, Collier NT, Vos JR (2006) Experiences creating three implementations of the repast agent modeling toolkit. ACM Trans Model Comput Simul 16(1):1–25

    Article  Google Scholar 

  • Pyka A, Fagiolo G (2007) Agent-based modelling: a methodology for neo-Schumpeterian economics. Elgar companion to neo-Schumpeterian economics [electronic resource], p 467

  • R Core Team (2015). R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna. https://www.r-project.org/

  • Rabin D, Forget C (1998) The Dictionary of Beer and Brewing. Taylor and Francis, Chicago

    Google Scholar 

  • Rixen M, Weigand J (2014) Agent-based simulation of policy induced diffusion of smart meters. Technol Forecast Soc Change 85:153–167

    Article  Google Scholar 

  • Stanley MH, Buldyrev SV, Havlin S, Mantegna RN, Salinger MA, Eugene Stanley H (1995) Zipf plots and the size distribution of firms. Econ Lett 49(4):453–457

    Article  Google Scholar 

  • Steenkamp J, Burgess S (2002) Optimum stimulation level and exploratory consumer behavior in an emerging consumer market. Int J Res Mark 19:131–150

    Article  Google Scholar 

  • Stigler GJ, Becker GS (1977) De gustibus non est disputandum. Am Econ Rev 67(2):76–90

    Google Scholar 

  • Valente M (2003) A model of bounded rational consumers with endogenous preferences. SIE, University of L’Aquila (working paper)

  • Valente M (2012) Evolutionary demand: a model for boundedly rational consumers. J Evolut Econ 22(5):1029–1080

    Article  Google Scholar 

  • Veblen TB (1899) The theory of the leisure class: an economic study in the evolution of institutions. Macmillan, New York

    Google Scholar 

  • Vogel H (1998) Entertainment industry economics. Cambridge University Press, Cambridge

    Google Scholar 

  • Windrum P (2005) Heterogeneous preferences and new innovation cycles in mature industries: the amateur camera industry 1955–1974. Ind Corp Change 14:1043–1074

    Article  Google Scholar 

  • Witt U (ed) (2001) Escaping satiation. The demand side of economic growth. Springer, Berlin

    Google Scholar 

  • Witt U (2005) From sensory to positivist utilitarianism and back: The rehabilitation of naturalistic conjectures in the theory of demand. Papers on economics and evolution. Max Planck Institute of Economics, Jena

Download references

Author information

Authors and Affiliations

  1. Department of Economic Analysis: Quantitative Economics, School of Business and Economics, Autonomous University of Madrid (UAM), E-3 205A, Francisco Tomás y Valiente Street, Number 5, 28049, Madrid, Spain

    Carlos M. Fernández-Márquez

  2. Department of Economic Analysis, Floor 3, School of Business and Economics, University of Zaragoza, Gran Vía Street, Number 2, 50005, Saragossa, Spain

    Francisco Fatas-Villafranca

  3. Department of Economic Analysis: Quantitative Economics, School of Business and Economics, Autonomous University of Madrid (UAM), E-3 312, Francisco Tomás y Valiente Street, Number 5, 28049, Madrid, Spain

    Francisco J. Vázquez

Authors
  1. Carlos M. Fernández-Márquez
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Francisco Fatas-Villafranca
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Francisco J. Vázquez
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Carlos M. Fernández-Márquez.

Appendix: Pseudo-code for replication

Appendix: Pseudo-code for replication

In this section we include a detailed algorithm that describes the specifications of the model in order to make it less ambiguous and reproducible for any researcher.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fernández-Márquez, C.M., Fatas-Villafranca, F. & Vázquez, F.J. A computational consumer-driven market model: statistical properties and the underlying industry dynamics. Comput Math Organ Theory 23, 319–346 (2017). https://doi.org/10.1007/s10588-016-9230-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10588-016-9230-4

Keywords

JEL Classification