Skip to main content

Advertisement

Springer Nature Link
Log in

A fuzzy polynomial fitting and mathematical programming approach for enhancing the accuracy and precision of productivity forecasting

  • Manuscript
  • Published:
Computational and Mathematical Organization Theory Aims and scope Submit manuscript

Abstract

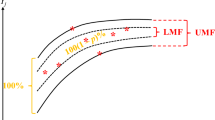
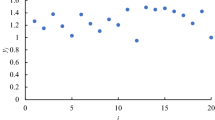
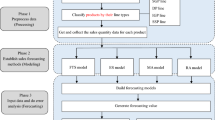
Forecasting future productivity is a critical task to every organization. However, the existing methods for productivity forecasting have two problems. First, the logarithmic or log-sigmoid value, rather than the original value, of productivity is dealt with. Second, the objective functions are not consistent with those adopted in practice. To address these problems, a fuzzy polynomial fitting and mathematical programming (FPF-MP) approach are proposed in this study. The FPF-MP approach solves two polynomial programming problems, based on the original value of productivity, in two steps to optimize accuracy and precision of forecasting future productivity, respectively. A real case was adopted to validate the effectiveness of the proposed methodology. According to the experimental results, the proposed FPF-MP approach outperformed six existing methods in improving the forecasting accuracy and precision.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Abbreviations

ANN:

Artificial neural network

ARIMA:

Autoregressive integrated moving average

DEA:

Data envelopment analysis

DRAM:

Dynamic random access memory

FCI:

Fuzzy collaborative intelligence

FLR:

Fuzzy linear regression

FNN:

Fuzzy neural network

FPF:

Fuzzy polynomial fitting

GMM:

Generalized method of moments

iMTA:

Institute for medical technology assessment

iPCQ:

iMTA productivity cost questionnaire

KKT:

Karush–Kuhn–Tucker

MAE:

Mean absolute error

MAPE:

Mean absolute percentage error

MP:

Mathematical programming

MPI:

Malmquist productivity index

NLP:

Nonlinear programming

PP:

Polynomial programming

RMSE:

Root mean square error

STB:

Smaller-the-better

TFN:

Triangular fuzzy number

VOLP:

Valuation of lost productivity

References

  • Bloom N, Draca M, Van Reenen J (2016) Trade induced technical change? The impact of Chinese imports on innovation, IT and productivity. Rev Econ Stud 83(1):87–117

    Article  Google Scholar 

  • Bouwmans C, Krol M, Brouwer W, Severens JL, Koopmanschap MA, Hakkaart L (2014) IMTA productivity cost questionnaire (IPCQ). Value Health 17(7):A550

    Article  Google Scholar 

  • Brandt L, Van Biesebroeck J, Zhang Y (2009) Creative accounting or creative destruction? Firm-level productivity growth in Chinese manufacturing. Working Paper 15152, NBER Working Paper Series

  • Chen T (2017a) New fuzzy method for improving the precision of productivity predictions for a factory. Neural Comput Appl 28:3507–3520

    Article  Google Scholar 

  • Chen T (2017b) Fitting an uncertain productivity learning process using an artificial neural network approach. Comput Math Org Theory (in press)

  • Chen T, Lin YC (2008) A fuzzy-neural system incorporating unequally important expert opinions for semiconductor yield forecasting. Int J Uncertain Fuzziness Knowl Based Syst 16(1):35–58

    Article  Google Scholar 

  • Chen T, Romanowski R (2014) Forecasting the productivity of a virtual enterprise by agent-based fuzzy collaborative intelligence—with Facebook as an example. Appl Soft Comput 24:511–521

    Article  Google Scholar 

  • Chen T, Wang YC (2016) Evaluating sustainable advantages in productivity with a systematic procedure. Int J Adv Manuf Technol 87:1435–1442

    Article  Google Scholar 

  • Chen T, Mikoláš Z, Wang Y-C (2016) Competitiveness assessment and enhancement for virtual organisations. Int J Technol Manag 70(1):1–3

    Article  Google Scholar 

  • Chou SY, Chang YH, Shen CY (2008) A fuzzy simple additive weighting system under group decision-making for facility location selection with objective/subjective attributes. Eur J Oper Res 189(1):132–145

    Article  Google Scholar 

  • Donoso S, Marin N, Vila MA (2006) Quadratic programming models for fuzzy regression. In: Proceedings of international conference on mathematical and statistical modeling in Honor of Enrique Castillo

  • Doraszelski U, Jaumandreu J (2013) R&D and productivity: estimating endogenous productivity. Rev Econ Stud 80(4):1338–1383

    Article  Google Scholar 

  • Earnest A, Chen MI, Ng D, Sin LY (2005) Using autoregressive integrated moving average (ARIMA) models to predict and monitor the number of beds occupied during a SARS outbreak in a tertiary hospital in Singapore. BMC Health Serv Res 5(1):36

    Article  Google Scholar 

  • Giachetti RE, Young RE (1997) A parametric representation of fuzzy numbers and their arithmetic operators. Fuzzy Sets Syst 91(2):185–202

    Article  Google Scholar 

  • Hägglöf K, Lindberg PO, Svensson L (1995) Computing global minima to polynomial optimization problems using Gröbner bases. J Global Optim 7(2):115–125

    Article  Google Scholar 

  • Hazewinkel M (2001) The algebra of quasi-symmetric functions is free over the integers. Adv Math 164(2):283–300

    Article  Google Scholar 

  • Hilton MF, Scuffham PA, Vecchio N, Whiteford HA (2010) Using the interaction of mental health symptoms and treatment status to estimate lost employee productivity. Aust N Z J Psychiatry 44(2):151–161

    Article  Google Scholar 

  • Kim CW, Lee K (2003) Innovation, technological regimes and organizational selection in industry evolution: a ‘history friendly model’ of the DRAM industry. Ind Corp Chang 12(6):1195–1221

    Article  Google Scholar 

  • Krol M, Brouwer W (2014) How to estimate productivity costs in economic evaluations. Pharmacoeconomics 32(4):335–344

    Article  Google Scholar 

  • Liu FHF, Wang PH (2008) DEA Malmquist productivity measure: Taiwanese semiconductor companies. Int J Prod Econ 112(1):367–379

    Article  Google Scholar 

  • Lv Y, Duan Y, Kang W, Li Z, Wang FY (2015) Traffic flow prediction with big data: a deep learning approach. IEEE Trans Intell Transp Syst 16(2):865–873

    Google Scholar 

  • Mattke S, Balakrishnan A, Bergamo G, Newberry SJ (2007) A review of methods to measure health-related productivity loss. Am J Manag Care 13(4):211

    Google Scholar 

  • Min JH, Lee YC (2005) Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters. Expert Syst Appl 28(4):603–614

    Article  Google Scholar 

  • Mirahadi F, Zayed T (2016) Simulation-based construction productivity forecast using neural-network-driven fuzzy reasoning. Autom Constr 65:102–115

    Article  Google Scholar 

  • Nocedal J, Wright SJ (2006) Numerical optimization. Springer, New York

    Google Scholar 

  • Peters G (1994) Fuzzy linear regression with fuzzy intervals. Fuzzy Sets Syst 63:45–55

    Article  Google Scholar 

  • Stevenson WJ (2002) Operations management. McGraw-Hill, New York

    Google Scholar 

  • Strömberg C, Aboagye E, Bergström G, Hagberg J, Lohela-Karlsson M (2017) Estimating the effect and economic impact of absenteeism, presenteeism, and work environment-related problems on reductions in productivity from a managerial perspective. Value in Health 20(8):1058–1064

    Article  Google Scholar 

  • Tanaka H, Watada J (1988) Possibilistic linear systems and their application to the linear regression model. Fuzzy Sets Syst 272:75–289

    Google Scholar 

  • Van Biesebroeck J (2007) Robustness of productivity estimates. J Ind Econ 55(3):529–569

    Article  Google Scholar 

  • Wang YF (2002) Predicting stock price using fuzzy grey prediction system. Expert Syst Appl 22(1):33–38

    Article  Google Scholar 

  • Wang Y-C, Chen T (2013) A fuzzy collaborative forecasting approach for forecasting the productivity of a factory. Adv Mech Eng Article No. 234571

Download references

Acknowledgements

This study was sponsored by the Ministry of Science and Technology, Taiwan.

Author information

Authors and Affiliations

  1. Department of Industrial Engineering and Management, National Chiao Tung University, 1001 University Road, Hsinchu, Taiwan

    Toly Chen

  2. Department of Industrial and Systems Engineering, Chang Yuan Christian University, 200 Chung Pei Road, Chung Li District, Taoyuan, Taiwan

    Chungwei Ou

  3. Department of Computer-aided Industrial Design, Overseas Chinese University, 100 Chiao Kung Rd., Taichung, Taiwan

    Yu-Cheng Lin

Authors
  1. Toly Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Chungwei Ou
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yu-Cheng Lin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Chungwei Ou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, T., Ou, C. & Lin, YC. A fuzzy polynomial fitting and mathematical programming approach for enhancing the accuracy and precision of productivity forecasting. Comput Math Organ Theory 25, 85–107 (2019). https://doi.org/10.1007/s10588-018-09287-w

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10588-018-09287-w

Keywords