Simulating the impact of social resource shortages on involution competition: involution, sit-up, and lying-flat strategies

Abstract

Along with COVID-19 ravaging almost 3 years, restricted working time and limited online working efficiency for the whole population results in social produced resource shortage sharpening. But how would the resource shortage affect the evolution of social population’s competition strategies? The concepts of involution, sit-up and lying-flat are put forward to describe such abnormal social competition phenomena and simulate individuals’ behaviour strategies, and a replicator dynamics game method with three strategies is proposed to solve the question. It is found that resource decrease and population increase result in involution degree relieving, while working time decreasing promotes involution. The increasing of sit-up cost and the utility of involution leads to severe involution, while the increase in involution cost will relieve involution. Moreover, it’s interesting to find that bad strategy drives out good when the resource becomes scarce. The robustness of results is tested by Derivative-free spectral approach, dual annealing and traversal method. The research sorts the evolution of involution concept and remaining qualitative & quantitative researches, and complements it from sit-up and lying-flat concept. The evolution of the three competition strategies is deduced from mathematics and proved by the simulation results. The research pays attention to the social involution concerns, in which the method and the results are meaningful to help give some insights for the deteriorative social competition. The R code and results can be reached at https://github.com/ZuoRX/replicator-dynamics/tree/main/codeA1.

Appendices

Appendix A The variants of replicator dynamics with three strategies

A denominator ${\bar{P}}$ added into Eq. (6) would not affect the final equilibrium result. When ${\bar{P}}=0$, the denominator is nonsense and is therefore abandoned.

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{y}}_D} = \frac{{{y_D}({P_D} - \bar{P})}}{{\bar{P}}}\\ {{\dot{z}}_C} = \frac{{{z_C}({P_C} - \bar{P})}}{{\bar{P}}}\\ {{\dot{x}}_L} = \frac{{{x_L}({P_L} - \bar{P})}}{{\bar{P}}} \end{array} \right. \end{aligned}$$

(A1)

A denominator ${\log (M + 1)}$ added into Eq. (6) would also not affect the final equilibrium result. But the influence of huge resource to relative payoffs can be controlled and the visualization in experimental part can be more vivid. While for simple rule, it is also not adopted.

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{y}}_D} = \frac{{{y_D}({P_D} - \bar{P})}}{{\log (M + 1)}}\\ {{\dot{z}}_C} = \frac{{{z_C}({P_C} - \bar{P})}}{{\log (M + 1)}}\\ {{\dot{x}}_L} = \frac{{{x_L}({P_L} - \bar{P})}}{{\log (M + 1)}} \end{array} \right. \end{aligned}$$

(A2)

Appendix B Transform replicator dynamics with three strategies into two strategies

1.1 Remove sit-up strategy

The proposed replicator dynamics with three strategies model is compatible to two strategies. When sit-up strategy is abandoned, ${z_C}{\mathrm{= }}1 - {x_L} - {y_{\textrm{D}}}{\mathrm{= }}0$ and ${{\textrm{N}}_{\textrm{C}}} = 0$. Even if $c \ne 0,{\beta _C} \ne 0$, the model is robust.

Therefore, the payoff of an individual with $N_D$ involution individuals, $N_C=0$ sit-up individuals and $N_L$ lying-flat individuals in current status is calculated by Eq. (B3).

$$\begin{aligned} \left\{ \begin{array}{l} {\pi _D} = \frac{{{\beta _D}d}}{{({N_D} + 1){\beta _D}d + 0 + {N_L}l}} \cdot M - d\\ {\pi _C} = \frac{{{\beta _C}c}}{{{N_D}{\beta _D}d + {\beta _C}c + {N_L}l}} \cdot M - c > 0\\ {\pi _L} = \frac{l}{{{N_D}{\beta _D}d + 0 + ({N_L} + 1)l}} \cdot M - l \end{array} \right. \end{aligned}$$

(B3)

The probabilities of selecting $N_D$, $N_C=N-N_L-N_D$, and $N_L$ individuals with high, medium, and low effort are therefore:

$$\begin{aligned} {p_{({N_D},{N_L})}} = \left( \begin{array}{c} N - 1\\ {N_D} \end{array} \right) \left( \begin{array}{c} {N_L}\\ {N_L} \end{array} \right) {y_{\textrm{D}}}^{{N_D}}{x_L}^{{N_L}}{(0)^0} = \left( \begin{array}{c} N - 1\\ {N_D} \end{array} \right) {y_{\textrm{D}}}^{{N_D}}{x_L}^{{N_L}} \end{aligned}$$

(B4)

The payoff expected value of three strategies, respectively $P_D$, $P_C$, and $P_L$ with all possible $N_D$s and $N_L$s is thus calculated by Eq. (B5).

$$\begin{aligned} \left\{ \begin{array}{l} {P_D} = \sum \limits _{{N_D} = 0}^{N - 1} {\sum \limits _{{N_L} = 0}^{{N_L}} {{p_{({N_D},{N_L})}}} } \cdot {\pi _D} = \sum \limits _{{N_D} = 0}^{N - 1} {{p_{({N_D},{N_L})}}} \cdot {\pi _D}\\ {P_C} = \sum \limits _{{N_D} = 0}^{N - 1} {\sum \limits _{{N_L} = 0}^{{N_L}} {{p_{({N_D},{N_L})}}} } \cdot {\pi _C} = \sum \limits _{{N_D} = 0}^{N - 1} {{p_{({N_D},{N_L})}}} \cdot {\pi _C} > 0\\ {P_L} = \sum \limits _{{N_D} = 0}^{N - 1} {\sum \limits _{{N_L} = 0}^{{N_L}} {{p_{({N_D},{N_L})}}} } \cdot {\pi _L} = \sum \limits _{{N_D} = 0}^{N - 1} {{p_{({N_D},{N_L})}}} \cdot {\pi _L} \end{array} \right. \end{aligned}$$

(B5)

The average payoff of three strategies for the whole individuals then follows Eq. (B6).

$$\begin{aligned} \bar{P} = {y_{\textrm{D}}}{P_D} + 0\cdot {P_C} + {x_L}{P_L} = {y_{\textrm{D}}}{P_D} + {x_L}{P_L} \end{aligned}$$

(B6)

And an individual’s payoff expectation value can also be calculated as:

$$\begin{aligned} \bar{P} = \frac{M}{N} - {y_{\textrm{D}}}d - 0 \cdot c - {x_L}l = \frac{M}{N} - {y_{\textrm{D}}}d - {x_L}l \end{aligned}$$

(B7)

As a result, the equilibrium values of the three strategies without sit-up strategy are

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{y}}_D} = {y_{\textrm{D}}}({P_D} - \bar{P})\\ {{\dot{z}}_C} = 0\cdot ({P_C} - \bar{P})\\ {{\dot{x}}_L} = {x_L}({P_L} - \bar{P}) \end{array} \right. = \left\{ \begin{array}{l} {{\dot{y}}_D} = {y_{\textrm{D}}}({P_D} - \bar{P})\\ {{\dot{x}}_L} = {x_L}({P_L} - \bar{P}) \end{array} \right. \end{aligned}$$

(B8)

1.2 Remove involution strategy

When sit-up strategy is abandoned, ${y_{\textrm{D}}}{\mathrm{= }}0$ and ${{\textrm{N}}_{\textrm{D}}} = 0$. Even if $d \ne 0,{\beta _D} \ne 0$, the model is robust.

Therefore, the payoff of an individual with $N_D=0$ involution individuals, $N_C$ sit-up individuals and $N_L$ lying-flat individuals in current status is calculated by Eq. (B9).

$$\begin{aligned} \left\{ \begin{array}{l} {\pi _D} = \frac{{{\beta _D}d}}{{{\beta _D}d + {N_C}{\beta _C}c + {N_L}l}} \cdot M - d > 0\\ {\pi _C} = \frac{{{\beta _C}c}}{{0 + ({N_C} + 1){\beta _C}c + {N_L}l}} \cdot M - c\\ {\pi _L} = \frac{l}{{0 + {N_C}{\beta _C}c + ({N_L} + 1)l}} \cdot M - l \end{array} \right. \end{aligned}$$

(B9)

The probabilities of selecting $N_D=0$, $N_C=N-N_L-N_D$, and $N_L$ individuals with high, medium, and low effort are therefore:

$$\begin{aligned} \begin{array}{l} {p_{({N_C},{N_L})}} = \left( \begin{array}{c} N - 1\\ 0 \end{array} \right) \left( \begin{array}{c} N - 1\\ {N_L} \end{array} \right) {y_{\textrm{D}}}^0{x_L}^{{N_L}}{(1 - 0 - {x_L})^{N - {N_L} - 1}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = \left( \begin{array}{c} N - 1\\ {N_L} \end{array} \right) {x_L}^{{N_L}}{(1 - {x_L})^{N - {N_L} - 1}} \end{array} \end{aligned}$$

(B10)

The payoff expected value of three strategies, respectively $P_D$,$P_C$, and $P_L$ with all possible $N_D=0$ and $N_L$s is thus calculated by Eq. (B11).

$$\begin{aligned} \left\{ \begin{array}{l} {P_D} = \sum \limits _{{N_D} = 0}^0 {\sum \limits _{{N_L} = 0}^{N - 1} {{p_{({N_C},{N_L})}}} } \cdot {\pi _D} = \sum \limits _{{N_L} = 0}^{N - 1} {{p_{({N_C},{N_L})}}} \cdot {\pi _D} > 0\\ {P_C} = \sum \limits _{{N_D} = 0}^0 {\sum \limits _{{N_L} = 0}^{N - 1} {{p_{({N_C},{N_L})}}} } \cdot {\pi _C} = \sum \limits _{{N_L} = 0}^{N - 1} {{p_{({N_C},{N_L})}}} \cdot {\pi _C}\\ {P_L} = \sum \limits _{{N_D} = 0}^0 {\sum \limits _{{N_L} = 0}^{N - 1} {{p_{({N_C},{N_L})}}} } \cdot {\pi _L} = \sum \limits _{{N_L} = 0}^{N - 1} {{p_{({N_C},{N_L})}}} \cdot {\pi _L} \end{array} \right. \end{aligned}$$

(B11)

The average payoff of three strategies for the whole individuals then follows Eq. (B12).

$$\begin{aligned} \bar{P} = 0\cdot {P_D} + (1 - {x_L} - 0){P_C} + {x_L}{P_L} = (1 - {x_L}){P_C} + {x_L}{P_L} \end{aligned}$$

(B12)

And an individual’s payoff expectation value can also be calculated as:

$$\begin{aligned} \bar{P} = \frac{M}{N} - 0 \cdot d - (1 - {x_L} - 0)c - {x_L}l = \frac{M}{N} - (1 - {x_L})c - {x_L}l \end{aligned}$$

(B13)

As a result, the equilibrium values for the three strategies without involution strategy are

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{y}}_D} = 0\cdot ({P_D} - \bar{P})\\ {{\dot{z}}_C} = {z_C}({P_C} - \bar{P})\\ {{\dot{x}}_L} = {x_L}({P_L} - \bar{P}) \end{array} \right. = \left\{ \begin{array}{l} {{\dot{z}}_C} = {z_C}({P_C} - \bar{P})\\ {{\dot{x}}_L} = {x_L}({P_L} - \bar{P}) \end{array} \right. \end{aligned}$$

(B14)

1.3 Remove lying-flat strategy

When lying-flat strategy is abandoned, ${x_L}{\mathrm{= }}0$ and ${{\textrm{N}}_{\textrm{L}}} = 0$. Even if $l \ne 0$, the model is robust.

Therefore, the payoff of an individual with $N_D$ involution individuals, $N_C$ sit-up individuals and $N_L=0$ lying-flat individuals in current status is calculated by Eq. (B15).

$$\begin{aligned} \left\{ \begin{array}{l} {\pi _D} = \frac{{{\beta _D}d}}{{({N_D} + 1){\beta _D}d + {N_C}{\beta _C}c + 0}} \cdot M - d\\ {\pi _C} = \frac{{{\beta _C}c}}{{{N_D}{\beta _D}d + ({N_C} + 1){\beta _C}c + 0}} \cdot M - c\\ {\pi _L} = \frac{l}{{{N_D}{\beta _D}d + {N_C}{\beta _C}c + l}} \cdot M - l > 0 \end{array} \right. \end{aligned}$$

(B15)

The relative utility of involution compared to sit-up is therefore $\beta = \frac{{{\beta _D}}}{{{\beta _C}}}$, and ${{\beta _C}} \ne 1$ do not affect the result.

The probabilities of selecting $N_D$, $N_C=N-N_L-N_D$, and $N_L$ individuals with high, medium, and low effort are therefore:

$$\begin{aligned} \begin{array}{l} {p_{({N_D},{N_C})}} = \left( \begin{array}{c} N - 1\\ {N_D} \end{array} \right) \left( \begin{array}{c} {N_C}\\ {N_C} \end{array} \right) {y_{\textrm{D}}}^{{N_D}}{0^0}{(1 - {y_D} - 0)^{N - {N_D} - 1}}\\ \;\;\;\;\;\;\;\;\;\;\;\; = \left( \begin{array}{c} N - 1\\ {N_D} \end{array} \right) {y_{\textrm{D}}}^{{N_D}}{(1 - {y_D})^{N - {N_D} - 1}} \end{array} \end{aligned}$$

(B16)

The payoff expected value of three strategies, respectively $P_D$,$P_C$, and $P_L$ with all possible $N_D$s and $N_L$s is thus calculated by Eq. (B17).

$$\begin{aligned} \left\{ \begin{array}{l} {P_D} = \sum \limits _{{N_D} = 0}^{N - 1} {\sum \limits _{{N_L} = 0}^0 {{p_{({N_D},{N_C})}}} } \cdot {\pi _D} = \sum \limits _{{N_D} = 0}^{N - 1} {{p_{({N_D},{N_C})}}} \cdot {\pi _D} > 0\\ {P_C} = \sum \limits _{{N_D} = 0}^{N - 1} {\sum \limits _{{N_L} = 0}^0 {{p_{({N_D},{N_C})}}} } \cdot {\pi _C} = \sum \limits _{{N_D} = 0}^{N - 1} {{p_{({N_D},{N_C})}}} \cdot {\pi _C}\\ {P_L} = \sum \limits _{{N_D} = 0}^{N - 1} {\sum \limits _{{N_L} = 0}^0 {{p_{({N_D},{N_C})}}} } \cdot {\pi _L} = \sum \limits _{{N_D} = 0}^{N - 1} {{p_{({N_D},{N_C})}}} \cdot {\pi _L} \end{array} \right. \end{aligned}$$

(B17)

The average payoff of three strategies for the whole individuals then follows Eq. (B18).

$$\begin{aligned} \bar{P} = {y_{\textrm{D}}}{P_D} + (1 - 0 - {y_{\textrm{D}}}){P_C} + 0 \cdot {P_L} = {y_{\textrm{D}}}{P_D} + (1 - {y_{\textrm{D}}}){P_C} \end{aligned}$$

(B18)

And an individual’s payoff expectation value can also be calculated as:

$$\begin{aligned} \bar{P} = \frac{M}{N} - {y_{\textrm{D}}}d - (1 - 0 - {y_{\textrm{D}}})c - 0 \cdot l = \frac{M}{N} - {y_{\textrm{D}}}d - (1 - {y_{\textrm{D}}})c \end{aligned}$$

(B19)

As a result, the equilibrium values for the three strategies without sit-up strategy are

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{y}}_D} = {y_{\textrm{D}}}({P_D} - \bar{P})\\ {{\dot{z}}_C} = {z_C}({P_C} - \bar{P})\\ {{\dot{x}}_L} = 0 \cdot ({P_L} - \bar{P}) \end{array} \right. = \left\{ \begin{array}{l} {{\dot{y}}_D} = {y_{\textrm{D}}}({P_D} - \bar{P})\\ {{\dot{z}}_C} = {z_C}({P_C} - \bar{P}) \end{array} \right. \end{aligned}$$

(B20)

Appendix C Scenario of involution utility declining

In reality, the utility of high effort is relative to the population who chooses the same strategy. Namely, the utility is relatively large when just a few individuals choose such strategy. However, given all staff in the department are working overtime and do not rest in the weekends, the possible utility of high effort, e.g., leader’s recognition or post promotion for example, can decrease to a very limited value.

Logistic function has been widely used to simulate population increasing with S shape curve. And Sigmoid function is a common format.

$$\begin{aligned} S(x) = \frac{1}{{1 + {e^{-x}}}} \end{aligned}$$

(C21)

This equation is the best mathematical model to describe the population growth law under the condition of limited resources. In the context of economic downturn, external resource is becoming very limited. The model is therefore suited to modeling the growth of the population who adopted high effort strategy.

In this experimental design, its variant is used to depict that the utility of an individual decreases with population increasing. Equation (C22) models the trend of high effort strategy community’s utility.

$$\begin{aligned} {{{\beta '}_D} = {\beta _D} - \frac{{{\beta _D} - {\beta _C}}}{{1 + {e^{ - k(\frac{{{N_D}}}{N} - \frac{1}{2})}}}}} \end{aligned}$$

(C22)

where ${{\beta _C}< {{\beta '}_D} < {\beta _D}}$. k is a parameter to adjust the curve degree and is set to 10 as default. And 1/2 is set to depict the utility value of the middle state when $N_C = \frac{1}{2}N$. ${\beta '}_D$ is close to $\beta _D$ when $N_D$ is close to 0, and close to $\beta _C$ when $N_C$ is close to N.

Equation (C23) models the trend of middle effort strategy community’s utility. And ${1< {{\beta '}_C} < {\beta _C}}$. $\beta '_C$ is close to $\beta _C$ when $N_C$ is close to 0, and close to 1, or the relative utility of lying-flat, when $N_C$ is close to N.

$$\begin{aligned} {{{\beta '}_C} = {\beta _C} - \frac{{{\beta _C} - 1}}{{1 + {e^{ - k(\frac{{{N_C}}}{N} - \frac{1}{2})}}}}} \end{aligned}$$

(C23)

Then the equilibrium value of the three strategies also follow Eqs. (1–6).

Appendix D Python-based implementation

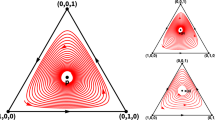
Another approach is adopted to further verify the result of the experiment. Instead of an infinite population, the game takes place among just three individuals. Figure 14 is done using a python package Egtplot (Mirzaev et al. 2018).

Fig. 14

The phase diagram for three strategies in three individuals. Given the default parameters of $M=10$, $\beta _D=1.5$, $\beta _C=1.1$, $d=4$, $c=1$ and $l=0.5$, the proportion of each strategy stabilizes at $x_D=1$, with $x_C=1$ as a saddle point

Except from the plot above, other sets of parameters are explored, and the proportion always stabilizes around $x_D=1$, $x_C=1$ or $x_L=1$. Namely, three strategies stabilize into two.