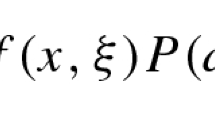Abstract
Stochastic linear programs can be solved approximately by drawing a subset of all possible random scenarios and solving the problem based on this subset, an approach known as sample average approximation (SAA). The value of the objective function at the optimal solution obtained via SAA provides an estimate of the true optimal objective function value. This estimator is known to be optimistically biased; the expected optimal objective function value for the sampled problem is lower (for minimization problems) than the optimal objective function value for the true problem. We investigate how two alternative sampling methods, antithetic variates (AV) and Latin Hypercube (LH) sampling, affect both the bias and variance, and thus the mean squared error (MSE), of this estimator. For a simple example, we analytically express the reductions in bias and variance obtained by these two alternative sampling methods. For eight test problems from the literature, we computationally investigate the impact of these sampling methods on bias and variance. We find that both sampling methods are effective at reducing mean squared error, with Latin Hypercube sampling outperforming antithetic variates. For our analytic example and the eight test problems we derive or estimate the condition number as defined in Shapiro et al. (Math. Program. 94:1–19, 2002). We find that for ill-conditioned problems, bias plays a larger role in MSE, and AV and LH sampling methods are more likely to reduce bias.
Similar content being viewed by others
References
Avramidis, A., Wilson, J.: Correlation-induction techniques for estimating quantiles in simulation experiments. Oper. Res. 46, 574–591 (1998)
Bailey, T.G., Jensen, P., Morton, D.P.: Response surface analysis of two-stage stochastic linear programming with recourse. Nav. Res. Logist. 46, 753–778 (1999)
Beale, E.M.: On minimizing a convex function subject to linear inequalities. J. R. Stat. Soc. B 17, 173–184 (1955)
Burnetas, A., Smith, C.: Adaptive ordering and pricing for perishable products. Oper. Res. 48, 436–443 (2000)
Czyzyk, J., Linderoth, J., Shen, J.: SUTIL: A utility library for handling stochastic programs. user’s manual (2005). Available at http://coral.ie.lehigh.edu/sutil
Dantzig, G.B.: Linear programming under uncertainty. Manag. Sci. 1, 197–206 (1955)
Dantzig, G.B.: Linear Programming and Extensions. Princeton University Press, Princeton (1963)
Diwekar, U.M., Kalagnanam, J.R.: Efficient sampling technique for optimization under uncertainty. AIChE J. 43, 440–447 (1997)
Dupačová, J., Wets, R.J.-B.: Asymptotic behavior of statistical estimators and of optimal solutions of stochastic optimization problems. Ann. Stat. 16, 1517–1549 (1988)
Foster, I., Kesselman, C.: Computational grids. In: Foster, I., Kesselman, C. (eds.) The Grid: Blueprint for a New Computing Infrastructure, pp. 15–52. Morgan Kaufmann, San Mateo (1999)
Higle, J.L.: Variance reduction and objective function evaluation in stochastic linear programs. INFORMS J. Comput. 10, 236–247 (1998)
Homem-de-Mello, T.: On rates of convergence for stochastic optimization problems under non-I.I.D. sampling. SIAM J. Optim. 19, 524–551 (2008)
Infanger, G.: Monte Carlo (importance) sampling within a Benders decomposition algorithm for stochastic linear programs. Ann. Oper. Res. 39, 69–95 (1992)
Janjarassuk, U., Linderoth, J.: Reformulation and sampling to solve a stochastic network interdiction problem. Networks 52, 120–132 (2008)
Law, A., Kelton, D.: Simulation Modeling and Analysis, 3rd edn. McGraw-Hill, Boston (2000)
Linderoth, J., Shapiro, A., Wright, S.: The empirical behavior of sampling methods for stochastic programming. Ann. Oper. Res. 142, 215–241 (2006)
Linderoth, J., Wright, S.: Implementing a decomposition algorithm for stochastic programming on a computational grid. Comput. Optim. Appl. 24, 207–250 (2003)
Litzkow, M.J., Livny, M., Mutka, M.W.: Condor—A hunter of idle workstations. In: Proceedings of the 8th International Conference on Distributed Computing Systems, pp. 104–111 (1988)
Louveaux, F., Smeers, Y.: Optimal investments for electricity generation: a stochastic model and a test problem. In: Ermoliev, Y., Wets, R.J.-B. (eds.) Numerical Techniques for Stochastic Optimization Problems, pp. 445–452. Springer, Berlin (1988)
Mak, W.K., Morton, D.P., Wood, R.K.: Monte Carlo bounding techniques for determining solution quality in stochastic programs. Oper. Res. Lett. 24, 47–56 (1999)
McKay, M.D., Beckman, R.J., Conover, W.J.: A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 21, 239–245 (1979)
Mulvey, J.M., Ruszczyński, A.: A new scenario decomposition method for large scale stochastic optimization. Oper. Res. 43, 477–490 (1995)
Norkin, V., Pflug, G., Ruszczyński, A.: A branch and bound method for stochastic global optimization. Math. Program. 83, 425–450 (1998)
Partani, A.: Adaptive jackknife estimators for stochastic programming. Ph.D. thesis, University of Texas at Austin (2007)
Partani, A., Morton, D., Popova, I.: Jackknife estimators for reducing bias in asset allocation. In: Perrone, L.F., Wieland, F.P., Liu, J., Lawson, B.G., Nicol, D.M., Fujimoto, R.M. (eds.) Proceedings of the 2006 Winter Simulation Conference, pp. 783–791. IEEE Press, New York (2006)
Powell, W., Topaloglu, H.: Fleet management. In: Wallace, S., Ziemba, W. (eds.) Applications of Stochastic Programming. MPS-SIAM Series on Optimization, pp. 185–216. SIAM, Philadelphia (2005)
Sen, S., Doverspike, R.D., Cosares, S.: Network planning with random demand. Telecommun. Syst. 3, 11–30 (1994)
Shapiro, A., Homem-de-Mello, T., Kim, J.: Conditioning of convex piecewise linear stochastic programs. Math. Program. 94, 1–19 (2002)
Van Slyke, R., Wets, R.J.-B.: L-shaped linear programs with applications to control and stochastic programming. SIAM J. Appl. Math. 17, 638–663 (1969)
Author information
Authors and Affiliations
Corresponding author
Electronic Supplementary Material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Freimer, M.B., Linderoth, J.T. & Thomas, D.J. The impact of sampling methods on bias and variance in stochastic linear programs. Comput Optim Appl 51, 51–75 (2012). https://doi.org/10.1007/s10589-010-9322-x
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-010-9322-x