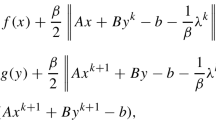Skip to main content
SpringerLink
Log in

Bregman operator splitting with variable stepsize for total variation image reconstruction

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

Abstract

This paper develops a Bregman operator splitting algorithm with variable stepsize (BOSVS) for solving problems of the form \(\min\{\phi(Bu) +1/2\|Au-f\|_{2}^{2}\}\), where ϕ may be nonsmooth. The original Bregman Operator Splitting (BOS) algorithm employed a fixed stepsize, while BOSVS uses a line search to achieve better efficiency. These schemes are applicable to total variation (TV)-based image reconstruction. The stepsize rule starts with a Barzilai-Borwein (BB) step, and increases the nominal step until a termination condition is satisfied. The stepsize rule is related to the scheme used in SpaRSA (Sparse Reconstruction by Separable Approximation). Global convergence of the proposed BOSVS algorithm to a solution of the optimization problem is established. BOSVS is compared with other operator splitting schemes using partially parallel magnetic resonance image reconstruction problems. The experimental results indicate that the proposed BOSVS algorithm is more efficient than the BOS algorithm and another split Bregman Barzilai-Borwein algorithm known as SBB.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Baraniuk, R., Steeghs, P.: Compressive radar imaging. In: 2007 IEEE Radar Conference, pp. 128–133 (2007)

    Chapter  Google Scholar 

  2. Barzilai, J., Borwein, J.M.: Two point step size gradient methods. IMA J. Numer. Anal. 8, 141–148 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  3. Block, K., Uecker, M., Frahm, J.: Undersampled radial MRI with multiple coils: iterative image reconstruction using a total variation constraint. Magn. Reson. Med. 57, 1086–1098 (2007)

    Article  Google Scholar 

  4. Chan, T.F., Golub, G.H., Mulet, P.: A nonlinear primal-dual method for total variationbased image restoration. SIAM J. Optim. 20, 1964–1977 (1999)

    MathSciNet  MATH  Google Scholar 

  5. Chen, Y., Hager, W.W., Huang, F., Phan, D.T., Ye, X., Yin, W.: Fast algorithms for image reconstruction with application to partially parallel MR imaging. SIAM J. Imaging Sci. 5, 90–118 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  6. Darbon, J., Sigelle, M.: A fast and exact algorithm for total variation minimization. In: Lecture Notes in Comput. Sci. IbPRIA, vol. 3522, pp. 351–359. Springer, Berlin (2005)

    Google Scholar 

  7. Donoho, D.: Compressed sensing. IEEE Trans. Inf. Theory 52, 351–359 (2006)

    Google Scholar 

  8. Gabay, D.: Applications of the method of multipliers to variational inequalities. In: Fortin, M., Glowinski, R. (eds.) Augmented Lagrange Methods: Applications to the Solution of Boundary-Valued Problems, pp. 299–331. North Holland, Amsterdam (1983)

    Chapter  Google Scholar 

  9. Goldstein, T., Osher, S.: The split Bregman method for L1 regularized problems. SIAM J. Imaging Sci. 2, 323–343 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hager, W.W., Phan, D.T., Zhang, H.: Gradient-based methods for sparse recovery. SIAM J. Imaging Sci. 4, 146–165 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  11. Hestenes, M.R.: Multiplier and gradient methods. J. Optim. Theory Appl. 4, 303–320 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  12. Huang, Y., Ng, M.K., Wen, Y.: A new total variation method for multiplicative noise removal. SIAM J. Imaging Sci. 2, 20–40 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  13. Li, Y., Santosa, F.: An affine scalling algorithm for minimizing total variation in image enhancement. Tech. Rep. TR94-1470, Cornell Theory Center, Cornell University, Ithaca, NY (1994)

  14. Lustig, M., Donoho, D., Pauly, J.M.: Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58, 1182–1195 (2007)

    Article  Google Scholar 

  15. Pruessmann, K., Weiger, M., Bornert, P., Boesiger, P.: Advances in sensitivity encoding with arbitrary k-space trajectories. Magn. Reson. Med. 46, 638–651 (2001)

    Article  Google Scholar 

  16. Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton (1970)

    MATH  Google Scholar 

  17. Rudin, L., Osher, S., Fatemi, E.: Non-linear total variation noise removal algorithm. Physica D 60, 259–268 (1992)

    Article  MATH  Google Scholar 

  18. Strong, D., Chan, T.: Edge preserving and scale-dependent properties of total variation regularization. Inverse Probl. 19, 165–187 (2003)

    Article  MathSciNet  Google Scholar 

  19. Vogel, C.R.: A multigrid method for total variation-based image denoising. In: Bowers, K., Lund, J. (eds.) Computation and Control IV. Progess in Systems and Control Theory, vol. 20, pp. 323–331. Birkhauser, Boston (1995)

    Chapter  Google Scholar 

  20. Vogel, C.R., Oman, M.E.: Iterative methods for total variation denoising. SIAM J. Sci. Comput. 17, 227–238 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  21. Wang, Y., Yang, J., Yin, W., Zhang, Y.: A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imaging Sci. 1, 248–272 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  22. Wright, S.J., Nowak, R.D., Figueiredo, M.A.T.: Sparse reconstruction by separable approximation. IEEE Trans. Signal Process. 57, 2479–2493 (2009)

    Article  MathSciNet  Google Scholar 

  23. Yang, J., Zhang, Y., Yin, W.: A fast alternating direction method for TVL1-L2 signal reconstruction from partial Fourier data. IEEE J. Sel. Top. Signal Process. 4, 288–297 (2010)

    Article  Google Scholar 

  24. Ye, X., Chen, Y., Huang, F.: Computational acceleration for MR image reconstruction in partially parallel imaging. IEEE Trans. Med. Imaging 30, 1055–1063 (2011)

    Article  Google Scholar 

  25. Zhang, X., Burger, M., Bresson, X., Osher, S.: Bregmanized nonlocal regularization for deconvolution and sparse reconstruction. SIAM J. Imaging Sci. 3, 253–276 (2011)

    Article  MathSciNet  Google Scholar 

  26. Zhang, X., Burger, M., Osher, S.: A unified primal-dual algorithm framework based on Bregman iteration. J. Sci. Comput. 46, 20–46 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  27. Zhu, M., Chan, T.: An efficient primal-dual hybrid gradient algorithm for total variation image restoration. Tech. Rep. 08-34, CAM UCLA (2008)

  28. Zhu, M., Wright, S., Chan, T.: Duality-based algorithms for total-variation-regularized image restoration. Comput. Optim. Appl. 47, 377–400 (2010)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors thank Invivo Corporation and Dr. Feng Huang for providing the PPI data used in the paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Florida, P.O. Box 118105, Gainesville, FL, 32611-8105, USA

    Yunmei Chen, William W. Hager & Maryam Yashtini

  2. School of Mathematics, Georgia Institute of Technology, 686 Cherry Street, Atlanta, GA, 30332-0160, USA

    Xiaojing Ye

  3. Department of Mathematics, Louisiana State University, Baton Rouge, LA, 70803-4918, USA

    Hongchao Zhang

Authors
  1. Yunmei Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. William W. Hager
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Maryam Yashtini
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiaojing Ye
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hongchao Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Maryam Yashtini.

Additional information

This research was partly supported by National Science Foundation grants 1115568 and 1016204, and by Office of Naval Research grant N00014-11-1-0068.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chen, Y., Hager, W.W., Yashtini, M. et al. Bregman operator splitting with variable stepsize for total variation image reconstruction. Comput Optim Appl 54, 317–342 (2013). https://doi.org/10.1007/s10589-012-9519-2

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10589-012-9519-2

Keywords

Search

Navigation