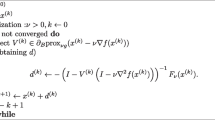Abstract
We propose a new stochastic first-order algorithm for solving sparse regression problems. In each iteration, our algorithm utilizes a stochastic oracle of the subgradient of the objective function. Our algorithm is based on a stochastic version of the estimate sequence technique introduced by Nesterov (Introductory lectures on convex optimization: a basic course, Kluwer, Amsterdam, 2003). The convergence rate of our algorithm depends continuously on the noise level of the gradient. In particular, in the limiting case of noiseless gradient, the convergence rate of our algorithm is the same as that of optimal deterministic gradient algorithms. We also establish some large deviation properties of our algorithm. Unlike existing stochastic gradient methods with optimal convergence rates, our algorithm has the advantage of readily enforcing sparsity at all iterations, which is a critical property for applications of sparse regressions.


Similar content being viewed by others
Notes
Although Lemma 5 in [6] is stated for \(\eta_{i}=\eta\sqrt{i+1}\), its conclusion and proof remain valid whenever η i is positive and nondecreasing in i.
References
Beck, A., Teboulle, M.: A fast iterative shrinkage-threshold algorithm for linear inverse problems. SIAM J. Image Sci. 2(1), 183–202 (2009)
Chung, K.L.: On a stochastic approximation method. Ann. Math. Stat. 25, 463–483 (1954)
Cotter, A., Shamir, O., Srebro, N., Sridharan, K.: Better mini-batch algorithms via accelerated gradient methods. In: Advances in Neural Information Processing Systems (NIPS) (2011)
Dekel, O., Gilad-Bachrach, R., Shamir, O., Xiao, L.: Optimal distributed online prediction using mini-batches. J. Mach. Learn. Res. 13, 165–202 (2012)
Duchi, J., Singer, Y.: Efficient online and batch learning using forward-backward splitting. J. Mach. Learn. Res. 10, 2873–2898 (2009)
Duchi, J.C., Bartlett, P.L., Wainwright, M.J.: Randomized smoothing for stochastic optimization. SIAM J. Optim. 22(2), 674–701 (2012)
Ermoliev, Y.: Stochastic quasigradient methods and their application to system optimization. Stochastics 9, 1–36 (1983)
Gaivoronski, A.A.: Nonstationary stochastic programming problems. Kybernetika 4, 89–92 (1978)
Hu, C., Kwok, J.T., Pan, W.: Accelerated gradient methods for stochastic optimization and online learning. In: Advances in Neural Information Processing Systems (NIPS) (2009)
Kiefer, J., Wolfowitz, J.: Stochastic estimation of the maximum of a regression function. Ann. Math. Stat. 23, 462–466 (1952)
Kushner, H.J., Yin, G.G.: Stochastic Approximation Algorithms and Applications. Springer, New York (2003)
Lan, G.: An optimal method for stochastic composite optimization. Math. Program. 133(1), 365–397 (2012)
Lan, G., Ghadimi, S.: Optimal stochastic approximation algorithm for strongly convex stochastic composite optimization, I: a generic algorithmic framework. SIAM J. Optim. 22(4), 1469–1492 (2012)
Lan, G., Ghadimi, S.: Optimal stochastic approximation algorithm for strongly convex stochastic composite optimization, II: shrinking procedures and optimal algorithms. SIAM J. Optim. 23(4), 2061–2069 (2013)
Langford, J., Li, L., Zhang, T.: Sparse online learning via truncated gradient. J. Mach. Learn. Res. 10, 2873–2908 (2009)
Lee, S., Wright, S.J.: Manifold identification in dual averaging methods for regularized stochastic online learning. J. Mach. Learn. Res. 13, 1705–1744 (2012)
Liu, J., Ji, S., Ye, J.: Multi-task feature learning via efficient ℓ 1/ℓ 2 norm minimization. In: The Twenty-Fifth Conference on Uncertainty in Artificial Intelligence (UAI) (2009)
Nemirovski, A., Juditsky, A., Lan, G., Shapiro, A.: Robust stochastic approximation approach to stochastic programming. SIAM J. Optim. 19(4), 1574–1609 (2009)
Nemirovski, A., Yudin, D.: On Cezari’s convergence of the steepest descent method for approximating saddle point of convex-concave functions. Soviet Mathematics Doklady 19 (1978)
Nemirovski, A., Yudin, D.: Problem Complexity and Method Efficiency in Optimization. Wiley, New York (1983)
Nesterov, Y.E.: Gradient methods for minimizing composite objective function. Technical report, CORE (2007)
Nesterov, Y.: Introductory Lectures on Convex Optimization: A Basic Course. Kluwer, Amsterdam (2003)
Nesterov, Y.: Smooth minimization of non-smooth functions. Math. Program. 103(1), 127–152 (2005)
Nesterov, Y.: Primal-dual subgradient methods for convex problems. Math. Program. 120, 221–259 (2009)
Pflug, G.C.: Optimization of Stochastic Models, the Interface Between Simulation and Optimization. Kluwer, Boston (1996)
Polyak, B.T., Juditsky, A.B.: Acceleration of stochastic approximation by averaging. SIAM J. Control Optim. 30, 838–855 (1992)
Polyak, B.T.: New stochastic approximation type procedures. Automat. Telemekh. 7, 98–107 (1990)
Pong, T.K., Tseng, P., Ji, S., Ye, J.: Trace norm regularization: reformulations, algorithms, and multi-task learning. SIAM J. Optim. 20(6), 3465–3489 (2010)
Robbins, H., Monro, S.: A stochastic approximation method. Ann. Math. Stat. 22(3), 400–407 (1951)
Ruszczynski, A., Syski, W.: A method of aggregate stochastic subgradients with on-line stepsize rules for convex stochastic programming problems. Math. Program. Stud. 28, 113–131 (1986)
Sacks, J.: Asymptotic distribution of stochastic approximation. Ann. Math. Stat. 29, 373–409 (1958)
Tibshirani, R.: Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B 58, 267–288 (1996)
Toh, K.-C., Yun, S.: An accelerated proximal gradient algorithm for nuclear norm regularized least squares problems. Pac. J. Optim. 6, 615–640 (2010)
Tseng, P.: On accelerated proximal gradient methods for convex-concave optimization. Technical report, University of Washington (2008)
Xiao, L.: Dual averaging methods for regularized stochastic learning and online optimization. J. Mach. Learn. Res. 11, 2543–2596 (2010)
Yuan, M., Lin, Y.: Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. B 68, 49–67 (2006)
Author information
Authors and Affiliations
Corresponding author
Appendix: Some technical proofs
Appendix: Some technical proofs
This section presents the proofs of Lemma 2, Lemma 4, and Proposition 1.
1.1 A.1 Proof of Lemma 2
According to the definition of \(\widehat{x}\), there is a \(\eta\in \partial h(\widehat{x})\) such that
By the convexity of h(x), we will have
It then follow from (2), (56) and (57) that
Notice that the inequalities above hold for any realization of stochastic gradient G(x,ξ). Hence, (16) holds almost surely. □
1.2 A.2 Proof of Lemma 4
By the choice of V 0(x), (20) holds for k=0 with \(V_{0}^{*}=\phi(x_{0})\), ϵ 0=0 and δ 0=0. Suppose we have \(V_{k}(x)=V_{k}^{*}+\frac{\gamma_{k}}{2}\|x-z_{k}\|^{2}+ \langle\epsilon _{k},x \rangle\). According to the updating equation (19), V k+1(x) is also a quadratic function whose coefficient on ∥x∥2 is \(\frac{(1-\alpha_{k})\gamma_{k}+\alpha_{k}\mu}{2}\). Therefore, V k+1(x) can definitely be represented as \(V_{k+1}(x)=V_{k+1}^{*}+\frac{\gamma_{k+1}}{2}\|x-z_{k+1}\|^{2}+ \langle\epsilon_{k+1},x \rangle\) with γ k+1=(1−α k )γ k +α k μ and some \(V_{k+1}^{*}\), z k+1 and ϵ k+1.
It follows from (19) that
We take the term \(T_{1}=\frac{(1-\alpha_{k})\gamma_{k}}{2}\|x-z_{k}\| ^{2}+\frac{\alpha_{k}\mu}{2}\|x-y_{k}\|^{2}+\alpha_{k} \langle g_{k},x-y_{k} \rangle\) out from V k+1(x) and consider it separately. We define γ k+1 and z k+1 according to (21) and (23), we get
(The last step follows from a straightforward, though somewhat tedious algebraic expansion.) Therefore, replacing T 1 in (58) with (59), we can rewrite V k+1(x) as
In order to represent V k+1(x) by the formulation (20), it suffices to define ϵ k+1 and \(V_{k+1}^{*}\) as (22) and (24). □
1.3 A.3 Proof of Proposition 1
We prove (13) is true by induction. According to Lemma 4, V k (x) is given by (20). Hence, we just need to prove \(V_{k}^{*}\geq\phi(x_{k})-B_{k}\). Since \(V_{0}^{*}=\phi(x_{0})\) and B 0=0, (13) is true when k=0. Suppose (13) is true for k. We are going to show that it is also true for k+1.
Dropping the non-negative term \(\frac{\mu}{2}\|y_{k}-z_{k}\|^{2}\) in (24) and applying the assumption \(V_{k}^{*}\geq\phi(x_{k})-B_{k}\), we can bound \(V_{k+1}^{*}\) from below as
According to Lemma 2 (with \(\widehat{x} = x_{k+1}, \; \bar{x} = y_{k}\)) and (17), we have
Applying this to ϕ(x k ) in (60), it follows that
Due to (26), the term T 2 above is zero. Hence, \(V_{k+1}^{*}\) can be bounded from below as
Here, the last inequality is from the definition of A k given by (28) and the following inequality
Hence, (13) holds for k+1. □
Rights and permissions
About this article
Cite this article
Lin, Q., Chen, X. & Peña, J. A sparsity preserving stochastic gradient methods for sparse regression. Comput Optim Appl 58, 455–482 (2014). https://doi.org/10.1007/s10589-013-9633-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-013-9633-9