Eigenvalue, quadratic programming, and semidefinite programming relaxations for a cut minimization problem

Abstract

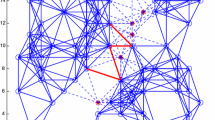
We consider the problem of partitioning the node set of a graph into k sets of given sizes in order to minimize the cut obtained using (removing) the kth set. If the resulting cut has value 0, then we have obtained a vertex separator. This problem is closely related to the graph partitioning problem. In fact, the model we use is the same as that for the graph partitioning problem except for a different quadratic objective function. We look at known and new bounds obtained from various relaxations for this NP-hard problem. This includes: the standard eigenvalue bound, projected eigenvalue bounds using both the adjacency matrix and the Laplacian, quadratic programming (QP) bounds based on recent successful QP bounds for the quadratic assignment problems, and semidefinite programming bounds. We include numerical tests for large and huge problems that illustrate the efficiency of the bounds in terms of strength and time.

Appendix: Notation for the SDP relaxation

In this appendix, we describes the constraints of the SDP relaxation (5.3) in detail.

• 1. The arrow linear transformation acts on $\mathcal {S}^{kn+1}$,

  $$\begin{aligned} \mathrm{arrow\,}(Y) := {{\mathrm{{diag}}}}(Y) - (0,Y_{0,1:kn})^T, \end{aligned}$$

  (9.1)

  $Y_{0,1:kn}$ is the vector formed from the last kn components of the first row (indexed by 0) of Y. The arrow constraint represents $X \in \mathcal {Z}$.

• 2. The norm constraints for $X\in \mathcal {E}$ are represented by the constraints with the two $(kn+1) \times (kn+1)$ matrices

  $$\begin{aligned} D_1:= & {} \left[ \begin{array}{c@{\quad }c} n &{} -e_{k}^T \otimes e_{n}^T \\ -e_{k} \otimes e_{n} &{} (e_{k}e_{k}^T) \otimes I_{n} \end{array} \right] ,\\ D_2:= & {} \left[ \begin{array}{c@{\quad }c} m^Tm &{} -m^T \otimes e_{n}^T \\ -m \otimes e_{n} &{} I_{k} \otimes (e_{n}e_{n}^T) \end{array} \right] , \end{aligned}$$

  where $e_j$ is the vector of ones of dimension j.

• 3. We let ${{\mathcal {G}}} _J$ represent the gangster operator on ${\mathcal {S}}^{kn+1}$, i.e., it shoots holes/zeros in a matrix,

  $$\begin{aligned} ({{\mathcal {G}}}_{J}(Y))_{ij}:= & {} \left\{ \begin{array}{l@{\quad }l} Y_{ij} &{} \hbox {if}~ (i,j)~ \hbox {or}~(j,i)~\in J\\ 0 &{} \hbox {otherwise,} \end{array} \right. \nonumber \\ J:= & {} \left\{ (i,j): i=(p-1)n+q,~~j=(r-1)n+q,\right. \nonumber \\&\left. \hbox {for}~~\begin{array}{l} p<r,~ p,r \in \{1,\ldots ,k\}\\ q \in \{1,\ldots ,n\} \end{array} \right\} . \end{aligned}$$

  (9.2)

  The gangster constraint represents the (Hadamard) orthogonality of the columns of X. The positions of the zeros are the diagonal elements of the off-diagonal blocks ${\bar{Y}}_{(ij)}, 1<i<j,$ of Y; see the block structure in (9.3) below.

• 4. Again, by abuse of notation, we use the symbols for the sets of constraints $\mathcal {D} _O,\mathcal {D} _e$ to represent the linear transformations in the SDP relaxation (5.3). Note that

  $$\begin{aligned} \langle \Psi , X^TX \rangle = {{\mathrm{{trace}}}}\, I X \Psi X^T = {{\mathrm{{vec}}}}(X)^T (\Psi \otimes I) {{\mathrm{{vec}}}}(X). \end{aligned}$$

  Therefore, the adjoint of $\mathcal {D} _O$ is made up of a zero row/column and $k^2$ blocks that are multiples of the identity:

  

  If Y is blocked appropriately as

  $$\begin{aligned} Y= \begin{bmatrix} Y_{00} |&Y_{0,:} \\ \hline Y_{:,0} |&{\bar{Y}} \end{bmatrix}, \quad {\bar{Y}} = \begin{bmatrix} {\bar{Y}}_{(11)}&{\bar{Y}}_{(12)}&\cdots&{\bar{Y}}_{(1k)}\\ {\bar{Y}}_{(21)}&{\bar{Y}}_{(22)}&\cdots&{\bar{Y}}_{(2k)}\\ \vdots&\ddots&\ddots&\vdots \\ {\bar{Y}}_{(k1)}&\ddots&\ddots&{\bar{Y}}_{(kk)} \end{bmatrix}, \end{aligned}$$

  (9.3)

  with each ${\bar{Y}}_{(ij)}$ being a $n\times n$ matrix, then

  $$\begin{aligned} \mathcal {D} _O(Y)= \left( {{\mathrm{{trace}}}}\, {\bar{Y}}_{(ij)}\right) \in \mathcal {S}^{k}. \end{aligned}$$

  (9.4)

  Similarly,

  $$\begin{aligned} \langle \phi , {{\mathrm{{diag}}}}(XX^T) \rangle =\langle {{\mathrm{{Diag}}}}(\phi ), XX^T \rangle ={{\mathrm{{vec}}}}(X)^T\left( I_k \otimes {{\mathrm{{Diag}}}}(\phi )\right) {{\mathrm{{vec}}}}(X). \end{aligned}$$

  Therefore we get the sum of the diagonal parts

  $$\begin{aligned} \mathcal {D} _e(Y)= \sum _{i=1}^k {{\mathrm{{diag}}}}{\bar{Y}}_{(ii)} \in {\mathbb {R}}^n. \end{aligned}$$

  (9.5)