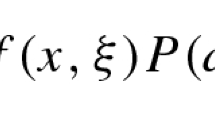Abstract
This paper presents a comparative computational study of the variance reduction techniques antithetic variates and Latin hypercube sampling when used for assessing solution quality in stochastic programming. Three Monte Carlo sampling-based procedures that provide point and interval estimators of optimality gap are considered: one that uses multiple replications, and two others with an alternative sample variance estimator that use single or two replications. Theoretical justification for using these alternative sampling techniques is discussed. In particular, we discuss asymptotic properties of the resulting estimators using Latin hypercube sampling for single- and two-replication procedures in detail. These theoretical considerations result in some subtle changes in the implementation of the procedures. A collection of two-stage stochastic linear test problems with different characteristics is used to empirically compare the three procedures for assessing solution quality with these variance reduction techniques.




Similar content being viewed by others
References
Attouch, H., Wets, R.: Approximation and convergence in nonlinear optimization. In: Mangasarian, O., Meyer, R., Robinson, S. (eds.) Nonlinear Programming 4, pp. 367–394. Academic Press, New York (1981)
Bailey, T., Jensen, P., Morton, D.: Response surface analysis of two-stage stochastic linear programming with recourse. Nav. Res. Log. 46, 753–778 (1999)
Bayraksan, G., Morton, D.: Assessing solution quality in stochastic programs. Math. Program. 108, 495–514 (2006)
Bayraksan, G., Morton, D.: A sequential sampling procedure for stochastic programming. Oper. Res. 59, 898–913 (2011)
Bayraksan, G., Pierre-Louis, P.: Fixed-width sequential stopping rules for a class of stochastic programs. SIAM J. Optim. 22, 1518–1548 (2012)
Beale, E.: On minimizing a convex function subject to linear inequalities. J. R. Stat. Soc. Ser. B 17, 173–184 (1955)
Bertocchi, M., Dupačová, J., Moriggia, V.: Sensitivity of bond portfolio’s behavior with respect to random movements in yield curve: a simulation study. Ann. Oper. Res. 99, 267–286 (2000)
Dantzig, G.: Linear programming under uncertainty. Manag. Sci. 1, 197–206 (1955)
Dantzig, G., Glynn, P.: Parallel processors for planning under uncertainty. Ann. Oper. Res. 22, 1–21 (1990)
Donohue, C., Birge, J.: An upper bound on the network recourse function. Working Paper. Department of Industrial and Operations Engineering, University of Michigan (1995)
Drew, S.: Quasi-Monte Carlo methods for stochastic programming. Ph.D. thesis, Northwestern University (2007)
Drew, S., Homem-de-Mello, T.: Quasi-Monte Carlo strategies for stochastic optimization. In: Proceedings of the 2006 Winter Simulation Conference, pp. 774–782 (2006)
Drew, S., Homem-de-Mello, T.: Some large deviations results for Latin hypercube sampling. Methodol. Comput. Appl. 14, 203–232 (2012)
Dupačová, J., Wets, R.B.: Asymptotic behavior of statistical estimators and of optimal solutions of stochastic optimization problems. Ann. Stat. 16, 1517–1549 (1988)
Freimer, M.B., Thomas, D.J., Linderoth, J.T.: The impact of sampling methods on bias and variance in stochastic linear programs. Comput. Optim. Appl. 51, 51–75 (2012)
Glynn, P., Infanger, G.: Simulation-based confidence bounds for two-stage stochastic programs. Math. Program. 138, 15–42 (2013)
Hackney, B., Infanger, G.: Private Communication (1994)
Higle, J.: Variance reduction and objective function evaluation in stochastic linear programs. INFORMS J. Comput. 10, 236–247 (1998)
Higle, J., Sen, S.: Duality and statistical tests of optimality for two stage stochastic programs. Math. Program. 75, 257–272 (1996)
Homem-de-Mello, T.: On rates of convergence for stochastic optimization problems under non-i.i.d. sampling. SIAM J. Optim. 19, 524–551 (2008)
Infanger, G.: Monte Carlo (importance) sampling within a Benders decomposition algorithm for stochastic linear programs. Ann. Oper. Res. 39, 69–95 (1992)
Keller, B., Bayraksan, G.: Scheduling jobs sharing multiple resources under uncertainty: a stochastic programming approach. IIE Trans. 42, 16–30 (2010)
Kenyon, A., Morton, D.: Stochastic vehicle routing with random travel times. Transp. Sci. 37, 69–82 (2003)
King, A., Rockafellar, R.: Asymptotic theory for solutions in statistical estimation and stochastic programming. Math. Oper. Res. 18, 148–162 (1993)
Koivu, M.: Variance reduction in sample approximations of stochastic programs. Math. Program. 103, 463–485 (2005)
Lan, G., Nemirovski, A., Shapiro, A.: Validation analysis of mirror descent stochastic approximation method. Math. Program. 134, 425–458 (2012)
Lemieux, C.: Monte Carlo and Quasi-Monte Carlo Sampling. Springer, New York (2009)
Linderoth, J., Shapiro, A., Wright, S.: The empirical behavior of sampling methods for stochastic programming. Ann. Oper. Res. 142, 215–241 (2006)
Loh, W.L.: On Latin hypercube sampling. Ann. Stat. 24, 2058–2080 (1996)
Mak, W., Morton, D., Wood, R.: Monte Carlo bounding techniques for determining solution quality in stochastic programs. Oper. Res. Lett. 24, 47–56 (1999)
McKay, M., Conover, R., Beckman, W.: A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 21, 239–245 (1979)
Mulvey, J., Ruszczyński, A.: A new scenario decomposition method for large scale stochastic optimization. Oper. Res. 43, 477–490 (1995)
Norkin, V., Pflug, G., Ruszczyński, A.: A branch and bound method for stochastic global optimization. Math. Program. 83, 425–450 (1998)
Owen, A.B.: A central limit theorem for Latin hypercube sampling. J. R. Stat. Soc. Ser. B 54, 541–551 (1992)
Owen, A.B.: Monte Carlo variance of scrambled net quadrature. SIAM J. Numer. Anal. 34, 1884–1910 (1997)
Pennanen, T., Koivu, M.: Epi-convergent discretizations of stochastic programs via integration quadratures. Numer. Math. 100, 141–163 (2005)
Pierre-Louis, P., Morton, D., Bayraksan, G.: A combined deterministic and sampling-based sequential bounding method for stochastic programming. In: Proceedings of the 2011 Winter Simulation Conference, pp. 4172–4183. Piscataway, New Jersey (2011)
Santoso, T., Ahmed, S., Goetschalckx, M., Shapiro, A.: A stochastic programming approach for supply chain network design under uncertainty. Eur. J. Oper. Res. 167, 96–115 (2005)
Sen, S., Doverspike, R., Cosares, S.: Network planning with random demand. Telecommun. J. 3, 11–30 (1994)
Shapiro, A.: Asymptotic properties of statistical estimators in stochastic programming. Ann. Stat. 17, 841–858 (1989)
Shapiro, A., Homem-de-Mello, T.: A simulation-based approach to two-stage stochastic programming with recourse. Math. Program. 81, 301–325 (1998)
Stockbridge, R.: Bias and variance reduction in assessing solution quality for stochastic programs. Ph.D. thesis, The University of Arizona (2013)
Stockbridge, R., Bayraksan, G.: A probability metrics approach for reducing the bias of optimality gap estimators in two-stage stochastic linear programming. Math. Program. 142, 107–131 (2013)
Verweij, B., Ahmed, S., Kleywegt, A., Nemhauser, G., Shapiro, A.: The sample average approximation method applied to stochastic vehicle routing problems: a computational study. Comput. Optim. Appl. 24, 289–333 (2003)
Acknowledgments
The authors are grateful to Tito Homem-de-Mello for providing reference [11], the coordinating editor and the referees for suggestions that improved the paper, and Andrzej Ruszczyński and Artur Świetanowski for access to their regularized decomposition code, which was used to solve the test problems. In addition, allocations of computer time from the Ohio Supercomputer Center (http://osc.edu/ark:/19495/f5s1ph73), UA Research Computing High Performance Computing (HPC) and High Throughput Computing (HTC) at the University of Arizona, and the Wayne State University High Performance Computing Services are gratefully acknowledged. This research has been partially funded by the National Science Foundation Grant CMMI-1345626.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Stockbridge, R., Bayraksan, G. Variance reduction in Monte Carlo sampling-based optimality gap estimators for two-stage stochastic linear programming. Comput Optim Appl 64, 407–431 (2016). https://doi.org/10.1007/s10589-015-9814-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-015-9814-9