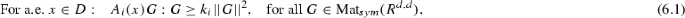Abstract
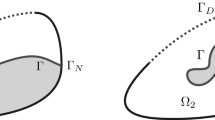
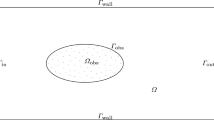
A mechanical equilibrium problem for a material consisting of two components with different densities is considered. Due to the heterogeneous material densities, the outer shape of the underlying workpiece can be changed by shifting the interface between the subdomains. In this paper, the problem is modeled as a shape design problem for optimally compensating unwanted workpiece changes. The associated control variable is the interface. Regularity results for transmission problems are employed for a rigorous derivation of suitable first-order optimality conditions based on the speed method. The paper concludes with several numerical results based on a spline approximation of the interface.










Similar content being viewed by others
Notes
Note that at this stage of investigation it is by no means necessary to assume that \(A_1,A_2\) are constant tensors. Indeed, assume \(A_1,A_2:D\rightarrow L({\mathbf {R}}^{3,3};{\mathbf {R}}^{3,3})\) and assuming
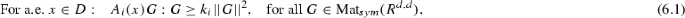
all calculations remain valid. Similarly, we could assume that \(\beta _1,\beta _2\in \text {L}^\infty (\text {D})\) instead of \(\beta _1,\beta _2 \in {\mathbf {R}}^+\).
References
Afraites, L., Dambrine, M., Kateb, D.: Shape methods for the transmission problem with a single measurement. Numer. Funct. Anal. Optim. 28(5–6), 519–551 (2007)
Allaire, G.: Shape Optimization by the Homogenization Method. Applied Mathematical Science, vol. 146. Springer, New York (2002)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs. The Clarendon Press Oxford University Press, New York (2000)
Antman, S.S.: Nonlinear Problems of Elasticity. Applied Mathematical Sciences, vol. 107, 2nd edn. Springer, New York (2005)
Chełminski, K., Hömberg, D., Kern, D.: On a thermomechanical model of phase transitions in steel. Adv. Math. Sci. Appl. 18, 119–140 (2008)
Chełminski, K., Hömberg, D., Petzold, T.: On a phase field approach towards distortion compensation. (In preparation) (2013)
Correa, R., Seeger, A.: Directional derivative of a minimax function. Nonlinear Anal. 9(1), 13–22 (1985)
Costabel, M., Dauge, M., Nicaise, S.: Corner singularities and analytic regularity for linear elliptic systems. Part I: Smooth domains. Prepublication IRMAR 10–09 (2010)
Delfour, M.C., Zolésio, J.-P.: Shapes and geometries, volume 22 of Advances in Design and Control. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, second edition. Metrics, analysis, differential calculus, and optimization (2011)
Ekeland, I., Temam, R.: Convex analysis and variational problems. North-Holland Publishing Co., Amsterdam. Translated from the French, Studies in Mathematics and its Applications, Vol. 1 (1976)
Evans, L.C.: Partial Differential Equations. Graduate Studies in Mathematics, vol. 19. American Mathematical Society, Providence (1998)
Giusti, E.: Minimal Surfaces and Functions of Bounded Variation. Monographs in Mathematics, vol. 80. Birkhäuser, Basel (1984)
Henrot, A., Pierre, M.: Variation et optimisation de formes. Mathématiques & Applications (Berlin) [Mathematics & Applications], vol. 48. Springer, Berlin. Une analyse géométrique. (A geometric analysis) (2005)
Hömberg, D., Kern, D.: The heat treatment of steel—a mathematical control problem. Materialwiss. Werkstofftech. 40, 438–442 (2009)
Hömberg, D., Volkwein, S.: Control of laser surface hardening by a reduced-order approach using proper orthogonal decomposition. Math. Comput. Model. 38, 1003–1028 (2003)
Lamboley, J., Pierre, M.: Structure of shape derivatives around irregular domains and applications. J. Convex Anal. 14(4), 807–822 (2007)
Pantz, O.: Sensibilité de l’équation de la chaleur aux sauts de conductivité. Comptes Rendus Math. Acad. Sci. Paris 341(5), 333–337 (2005)
Schüttenberg, S., Hunkel, M., Fritsching, U., Zoch, H.-W.: Controlling of distortion by means of quenching in adapted jet-fields. In: Zoch, H.-W., Lübben, Th (eds.) Proceedings of the 1st International Conference on Distortion Engineering - IDE 2005. Bremen, Germany, pp. 389–396. IWT, Bremen (2005)
Shi, P., Wright, S.: Higher integrability of the gradient in linear elasticity. Math. Ann. 299(1), 435–448 (1994)
Sturm, Kevin: Minimax Lagrangian approach to the differentiability of nonlinear PDE constrained shape functions without saddle point assumption. SIAM J. Control Optim. 53(4), 2017–2039 (2015)
Thoben, K.-D., Lübben, T., Clausen, B., Prinz, C., Schulz, A., Rentsch, R., Kusmierz, R., Nowag, L., Surm, H., Frerichs, F., Hunkel, M., Klein, D., Mayr, P.: “Distortion Engineering”: Eine systemorientierte Betrachtung des Bauteilverzugs. HTM 57, 276–282 (2002)
Ziemer, W.P.: Weakly Differentiable Functions, Graduate Texts in Mathematics. Sobolev Spaces and Functions of Bounded Variation, vol. 120. Springer, New York (1989)
Acknowledgments
This work was partially supported by the DFG Research Center Matheon. M.H. further acknowledges support through the FWF-START-Project Y305 “Interfaces and Free Boundaries” as well as the FWF-SFB F32 “Mathematical Optimization and Its Applications in Biomedical Sciences”.
Author information
Authors and Affiliations
Corresponding author
Appendix: Proof of Theorem 2.1
Appendix: Proof of Theorem 2.1
The result concerning higher regularity is a direct consequence of [8, Theorem 5.3.8]. Here, we show that the Eq. (2.5) indeed has a unique solution for every \(\chi \in \text {X}(\text {D})\). This can be seen as follows:Footnote 1 Since \(A_1, A_2\) are positive definite with coercivity constants \(k_1>k_2>0\) and from Korns inequality (with constant \(\theta _{K}>0\)) it follows that there exist constants \(C,\theta >0\), independent of \(\chi \), such that for all \(\varvec{\varphi }\in H^1(\text {D};{\mathbf {R}}^d)\)
where \(\theta :=k_2 \theta _K\) and
Thus the Lemma of Lax and Milgram (see [11, pp. 297–299, Theorem 1]) guarantees the unique solvability of the variational problem:
Since \(\varvec{\varphi }\mapsto \int _{\text {D}}\beta _\chi \mathrm{\, div\,}(\varvec{\varphi })\, dx\in \mathbf {\mathcal {W}}^{-1}\) according to the Lemma of Lax and Milgram
Notice that the constants are independent of \(\Omega \). In order to see this a priori bound, recall \(\chi \subset \text {X}(\text {D})\) and let \(\mathbf {u}_{\chi }\) denote the corresponding solution to (2.5). Using (6.2) we compute
with \(C:=\max \{\beta _1,\beta _2\}\sqrt{3|D|}/\theta \).
Rights and permissions
About this article
Cite this article
Sturm, K., Hintermüller, M. & Hömberg, D. Distortion compensation as a shape optimisation problem for a sharp interface model. Comput Optim Appl 64, 557–588 (2016). https://doi.org/10.1007/s10589-015-9816-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-015-9816-7