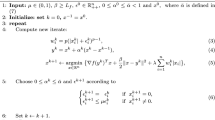Skip to main content
Springer Nature Link
Log in

Iteratively reweighted \(\ell _1\) algorithms with extrapolation

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

Abstract

Iteratively reweighted \(\ell _1\) algorithm is a popular algorithm for solving a large class of optimization problems whose objective is the sum of a Lipschitz differentiable loss function and a possibly nonconvex sparsity inducing regularizer. In this paper, motivated by the success of extrapolation techniques in accelerating first-order methods, we study how widely used extrapolation techniques such as those in Auslender and Teboulle (SIAM J Optim 16:697–725, 2006), Beck and Teboulle (SIAM J Imaging Sci 2:183–202, 2009), Lan et al. (Math Program 126:1–29, 2011) and Nesterov (Math Program 140:125–161, 2013) can be incorporated to possibly accelerate the iteratively reweighted \(\ell _1\) algorithm. We consider three versions of such algorithms. For each version, we exhibit an explicitly checkable condition on the extrapolation parameters so that the sequence generated provably clusters at a stationary point of the optimization problem. We also investigate global convergence under additional Kurdyka–Łojasiewicz assumptions on certain potential functions. Our numerical experiments show that our algorithms usually outperform the general iterative shrinkage and thresholding algorithm in Gong et al. (Proc Int Conf Mach Learn 28:37–45, 2013) and an adaptation of the iteratively reweighted \(\ell _1\) algorithm in Lu (Math Program 147:277–307, 2014, Algorithm 7) with nonmonotone line-search for solving random instances of log penalty regularized least squares problems in terms of both CPU time and solution quality.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. Note that when f is the least squares loss function and \(\Phi (|\cdot |)\) is the MCP or SCAD function, the function \(f(\cdot )+\Phi (|\cdot |)\) is not level-bounded (though it necessarily has a minimizer). However, the level-boundedness of F can still be enforced by picking C to be a huge box, i.e., \(C = [-M,M]^n\) for a sufficiently large \(M > 0\) so that C intersects \(\hbox {Arg min}_{x}\{f(x) + \Phi (|x|)\}\). For this choice of C, the optimal value of F is the same as that of \(f(\cdot )+\Phi (|\cdot |)\).

  2. Here and throughout, \(\phi '_+(t)\) denotes the right-hand derivative, i.e., \(\phi '_+(t):= \lim _{h\downarrow 0}\frac{\phi (t + h) - \phi (t)}{h}\).

  3. The condition \(\sup _k\beta _k<1\) is crucial in our analysis below for inducing “sufficient descent” of \(H_1\); see (8) below. However, note that this condition does not cover the choice of extrapolation parameters used in FISTA without restart, whose extrapolation parameters satisfy \(\sup _k\beta _k=1\).

  4. In our experiments, this quantity is computed in matlab with code lambda=norm(A*A’), when \( m<2000\) and by opts.issym = 1; lambda = eigs(A*A’,1,’LM’,opts); otherwise.

References

  1. Attouch, H., Bolte, J.: On the convergence of the proximal algorithm for nonsmooth functions invoving analytic features. Math. Program. 116, 5–16 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  2. Attouch, H., Bolte, J., Redont, P., Soubeyran, A.: Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the Kurdyka–Łojasiewicz inequality. Math. Oper. Res. 35, 438–457 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  3. Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward–backward splitting, and regularized Gauss–Seidel methods. Math. Program. 137, 91–129 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  4. Auslender, A., Teboulle, M.: Interior gradient and proximal methods for convex and conic optimization. SIAM J. Optim. 16, 697–725 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  5. Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2, 183–202 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  6. Becker, S., Candès, E.J., Grant, M.C.: Templates for convex cone problems with applications to sparse signal recovery. Math. Program. Comput. 3, 165–218 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bolte, J., Daniilidis, A., Lewis, A.: The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J. Optim. 17, 1205–1223 (2007)

    Article  MATH  Google Scholar 

  8. Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 146, 459–494 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  9. Borwein, J., Lewis, A.: Convex Analysis and Nonlinear Optimization, 2nd edn. Springer, Berlin (2006)

    Book  MATH  Google Scholar 

  10. Borwein, J., Zhu, Q.: Techniques in Variational Analysis. Springer, Berlin (2005)

    MATH  Google Scholar 

  11. Candès, E.J., Wakin, M.B., Boyd, S.P.: Enhancing sparsity by reweighted \(\ell _1\) minimization. J. Fourier Anal. Appl. 14, 877–905 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  12. Candès, E.J., Tao, T.: Decoding by linear programming. IEEE Trans. Inf. Theory 51, 4203–4215 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  13. Chartrand, R., Yin, W.: Iteratively reweighted algorithms for compressive sensing. In: IEEE International Conferenceon Acoustics, Speech and Signal Processing (2008)

  14. Chen, X., Lu, Z., Pong, T.K.: Penalty methods for a class of non-Lipschitz optimization problems. SIAM J. Optim. 26, 1465–1492 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  15. Chen, X., Womersley, R.: Spherical designs and nonconvex minimization for recovery of sparse signals on the sphere. SIAM J. Imaging Sci. 11, 1390–1415 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  16. Chen, X., Zhou, W.: Convergence of the reweighted \(\ell _1\) minimization algorithm for \(\ell _2-\ell _p\) minimization. Comput. Optim. Appl. 59, 47–61 (2014)

    Article  MathSciNet  Google Scholar 

  17. Drusvyatskiy, D., Paquette, C.: Efficiency ofminimizing compositions of convex functions and smooth maps. To appear in Math. Program. https://doi.org/10.1007/s10107-018-1311-3

  18. Facchinei, F., Pang, J.-S.: Finite-Dimensional Variational Inequalities and Complementarity Problems, vol. I. Springer, New York (2013)

    MATH  Google Scholar 

  19. Fan, J., Li, R.: Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96, 1348–1360 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  20. Foucart, S., Lai, M.: Sparsest solutions of undertermined linear systems via \(l_p\)-minimization for \(0<q\le 1\). Appl. Comput. Harmonic Anal. 26, 395–407 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  21. Foucart, S., Rauhut, H.: A Mathematical Introduction to Compressive Sensing. Springer, New York (2013)

    Book  MATH  Google Scholar 

  22. Ghadimi, S., Lan, G.: Accelerated gradient methods for nonconvex nonlinear and stochastic programming. Math. Program. 156, 59–99 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  23. Gong, P., Zhang, C., Lu, Z., Huang, J.Z., Ye, J.: A general iterative shrinkage and thresholding algorithm for non-convex regularized optimization problems. Proc. Int. Conf. Mach. Learn. 28, 37–45 (2013)

    Google Scholar 

  24. Lan, G., Lu, Z., Monteiro, R.D.C.: Primal-dual first-order methods with \(O(1/\epsilon )\) iteration-complexity for cone programming. Math. Program. 126, 1–29 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  25. Lu, Z.: Iterative reweighted minimization methods for \(l_p\) regularized unconstrained nonlinear programming. Math. Program. 147, 277–307 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  26. Nesterov, Y.: A method for solving the convex programming problem with convergence rate \(O(1/k^2)\). Dokl. Akad. Nauk. SSSR 269, 543–547 (1983)

    MathSciNet  Google Scholar 

  27. Nesterov, Y.: Introductory Lectures on Convex Programming. Kluwer Academic Publisher, Dordrecht (2004)

    Book  MATH  Google Scholar 

  28. Nesterov, Y.: Primal-dual subgradient methods for convex problems. Math. Program. 120, 221–259 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  29. Nesterov, Y.: Gradient methods for minimizing composite objective function. Math. Program. 140, 125–161 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  30. Ochs, P., Chen, Y., Brox, T., Pock, T.: iPiano: inertial proximal algorithm for non-convex optimization. SIAM J. Imaging Sci. 7, 1388–1419 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  31. O’Donoghue, B., Candès, E.J.: Adaptive restart for accelerated gradient schemes. Found. Comput. Math. 15, 715–732 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  32. Pock, T., Sabach, S.: Inertial proximal alternating linearized minimization (iPALM) for nonconvex and nonsmooth problems. SIAM J. Imaging Sci. 9, 1756–1787 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  33. Polyak, B.T.: Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. 4, 1–17 (1964)

    Article  Google Scholar 

  34. Rockafellar, R.T., Wets, R.J.-B.: Variational Analysis. Springer, Berlin (2009). (3rd printing)

    MATH  Google Scholar 

  35. Tseng, P.: Approximation accuracy, gradient methods and error bound for structured convex optimization. Math. Program. 125, 263–295 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  36. Tibshirani, R.: Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B 58, 267–288 (1996)

    MathSciNet  MATH  Google Scholar 

  37. Wen, B., Chen, X., Pong, T.K.: A proximal difference-of-convex algorithm with extrapolation. Comput. Optim. Appl. 69, 297–324 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  38. Wipf, D., Nagarajan, S.: Iterative reweighted \(\ell _1\) and \(\ell _2\) methods for finding sparse solutions. IEEE J. Sel. Topics Signal Process. 4, 317–329 (2010)

    Article  Google Scholar 

  39. Wright, S.J., Nowak, R., Figueiredo, M.A.T.: Sparse reconstruction by separable approximation. IEEE Trans. Signal Process. 57, 2479–2493 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  40. Xu, Y., Yin, W.: A block coordinate descent method for regularized multiconvex optimization with applications to nonnegative tensor factorization and completion. SIAM J. Imaging Sci. 6, 1758–1789 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  41. Zhang, C.: Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 38, 894–942 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  42. Zhao, Y., Li, D.: Reweighted \(\ell _1\)-minimization for sparse solutions to underdetermined linear systems. SIAM J. Optim. 22, 1065–1088 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  43. Zou, H., Trevor, H.: Regularization and variable selection via the elastic net. J. R. Stat. Soc. B 67, 301–320 (2005)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, The Hong Kong Polytechnic University, Hung Hom, Hong Kong

    Peiran Yu & Ting Kei Pong

Authors
  1. Peiran Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ting Kei Pong
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ting Kei Pong.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Ting Kei Pong: This author’s work was supported in part by Hong Kong Research Grants Council PolyU153085/16p.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, P., Pong, T.K. Iteratively reweighted \(\ell _1\) algorithms with extrapolation. Comput Optim Appl 73, 353–386 (2019). https://doi.org/10.1007/s10589-019-00081-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10589-019-00081-1

Keywords