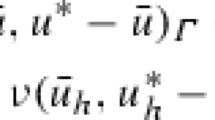Abstract
In this paper, we analyze optimal control problems governed by an elliptic partial differential equation, in which the control acts as the Dirichlet data. Box constraints for the controls are imposed and the cost functional involves the state and possibly a sparsity-promoting term, but not a Tikhonov regularization term. Two different discretizations are investigated: the variational approach and a full discrete approach. For the latter, we use continuous piecewise linear elements to discretize the control space and numerical integration of the sparsity-promoting term. It turns out that the best way to discretize the state equation is to use the Carstensen quasi-interpolant of the boundary data, and a new discrete normal derivative of the adjoint state must be introduced to deal with this. Error estimates, optimization procedures and examples are provided.



Similar content being viewed by others
References
Apel, T., Mateos, M., Pfefferer, J., Rösch, A.: On the regularity of the solutions of Dirichlet optimal control problems in polygonal domains. SIAM J. Control Optim. 53(6), 3620–3641 (2015). https://doi.org/10.1137/140994186
Apel, T., Nicaise, S., Pfefferer, J.: Discretization of the Poisson equation with non-smooth data and emphasis on non-convex domains. Numer. Methods Partial Diff. Equ. 32(5), 1433–1454 (2016). https://doi.org/10.1002/num.22057
Berggren, M.: Approximations of very weak solutions to boundary-value problems. SIAM J. Numer. Anal. 42(2), 860–877 (2004). https://doi.org/10.1137/S0036142903382048
Bramble, J.H., Pasciak, J.E., Schatz, A.H.: The construction of preconditioners for elliptic problems by substructuring. I. Math. Comp. 47(175), 103–134 (1986). https://doi.org/10.2307/2008084
Carstensen, C..: Quasi-interpolation and a posteriori error analysis in finite element methods. M2AN Math. Model. Numer. Anal. 33(6), 1187–1202 (1999)
Casas, E.: Second order analysis for bang-bang control problems of PDEs. SIAM J. Control Optim. 50(4), 2355–2372 (2012). https://doi.org/10.1137/120862892
Casas, E.: A review on sparse solutions in optimal control of partial differential equations. SEMA J. 74(3), 319–344 (2017). https://doi.org/10.1007/s40324-017-0121-5
Casas, E., Clason, C., Kunisch, K.: Approximation of elliptic control problems in measure spaces with sparse solutions. SIAM J. Control Optim. 50(4), 1735–1752 (2012). https://doi.org/10.1137/110843216
Casas, E., Herzog, R., Wachsmuth, G.: Approximation of sparse controls in semilinear equations by piecewise linear functions. Numer. Math. 122(4), 645–669 (2012). https://doi.org/10.1007/s00211-012-0475-7
Casas, E., Mateos, M.: Critical cones for sufficient second order conditions in PDE constrained optimization. SIAM J. Optim. 30(1), 585–603 (2020). https://doi.org/10.1137/19M1258244
Casas, E., Mateos, M.: State error estimates for the numerical approximation of sparse distributed control problems in the absence of Tikhonov regularization. Vietnam J. Math. (2021) (to appear)
Casas, E., Mateos, M., Raymond, J.P.: Penalization of Dirichlet optimal control problems. ESAIM Control Optim. Calc. Var. 15(4), 782–809 (2009). https://doi.org/10.1051/cocv:2008049
Casas, E., Raymond, J.P.: Error estimates for the numerical approximation of Dirichlet boundary control for semilinear elliptic equations. SIAM J. Control Optim. 45(5), 1586–1611 (2006). https://doi.org/10.1137/050626600
de los Reyes, J..C.., Meyer, C.., Vexler, B..: Finite element error analysis for state-constrained optimal control of the Stokes equations. Control Cybern. 37(2), 251–284 (2008)
Deckelnick, K., Hinze, M.: A note on the approximation of elliptic control problems with bang-bang controls. Comput. Optim. Appl. 51(2), 931–939 (2012). https://doi.org/10.1007/s10589-010-9365-z
Grisvard, P.: Elliptic Problems in Nonsmooth Domains, Monographs and Studies in Mathematics, vol. 24. Pitman (Advanced Publishing Program), Boston, MA (1985)
Mateos, M.: Optimization methods for Dirichlet control problems. Optimization 67(5), 585–617 (2018). https://doi.org/10.1080/02331934.2018.1426578
May, S., Rannacher, R., Vexler, B.: Error analysis for a finite element approximation of elliptic Dirichlet boundary control problems. SIAM J. Control Optim. 51(3), 2585–2611 (2013). https://doi.org/10.1137/080735734
Pieper, K.: Finite Element Discretization and Efficient Numerical Solution of Elliptic and Parabolic Sparse Control Problems. Ph.D. thesis, Technische Universität München (2015)
Pörner, F., Wachsmuth, D.: Tikhonov regularization of optimal control problems governed by semi-linear partial differential equations. Math. Control Relat. Fields 8(1), 315–335 (2018). https://doi.org/10.3934/mcrf.2018013
Qui, N.T., Wachsmuth, D.: Stability for bang-bang control problems of partial differential equations. Optimization 67(12), 2157–2177 (2018). https://doi.org/10.1080/02331934.2018.1522634
Rösch, A., Wachsmuth, G.: Mass lumping for the optimal control of elliptic partial differential equations. SIAM J. Numer. Anal. 55(3), 1412–1436 (2017). https://doi.org/10.1137/16M1074473
Stadler, G.: Elliptic optimal control problems with \(L^1\)-control cost and applications for the placement of control devices. Comput. Optim. Appl. 44(2), 159–181 (2009). https://doi.org/10.1007/s10589-007-9150-9
Acknowledgements
The author was partially supported by Spanish Ministerio de Economía y Competitividad under research project MTM2017-83185-P.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: On the regulairty of the conormal derivative
Appendix A: On the regulairty of the conormal derivative
Let \(\phi _g\in H^2(\varOmega )\cap H^1_0(\varOmega )\) be the solution of (2). Let us prove in detail that \(\partial _{\nu _{{A^*}}}\phi _g\in H^{1/2}(\varGamma )\).
Let us denote \((S_j)_{0\le j\le N_S}\) the vertices of \(\varOmega \), numbered counterclockwise and with the convention that \(S_0=S_{N_S}\). Each side of \(\varGamma \) is denoted \(\varGamma _j = [S_{j-1},S_j]\), where \(1\le j\le N_S\). The trace of \(\nabla \phi _g\) on \(\varGamma \) belongs to \((H^{1/2}(\varGamma ))^2\). Thus the trace of \(\nabla \phi _g\) on \(\varGamma _j\) belongs to \((H^{1/2}(\varGamma _j))^2\) and the Lipschitz regularity of the coefficients \(a_{ij}\) implies that \(\partial _{\nu _{{A^*}}} \phi _g\in H^{1/2}(\varGamma _j)\). Moreover we have the estimate
To show that \(\partial _{\nu _{{A^*}}}\phi _g\) belongs to \(H^{1/2}(\varGamma )\) we have to analyze the behaviour at the corners \(S_j=\varGamma _j\cap \varGamma _{j+1}\). Following [16], we parametrize \(\varGamma _{j+1}\) by setting \(x_j(\sigma )= S_j + \frac{\sigma }{|\varGamma _{j+1}|}(S_{j+1}- S_j )\) with \(0\le \sigma \le |\varGamma _{j+1}|\), and \(\varGamma _{j}\) by \(x_j(-\sigma )= S_j - \frac{\sigma }{|\varGamma _{j}|}(S_{j}- S_{j-1} )\) with \(0\le \sigma \le |\varGamma _j|\). For \(0\le \sigma \le \delta _j=\min \{|\varGamma _j|,|\varGamma _{j+1}|\}\), \(x_j(\sigma )\in \varGamma _{j+1}\), \(x_j(-\sigma )\in \varGamma _{j}\) and \(|x_j(\sigma )-S_j|=|x_j(-\sigma )-S_j|=\sigma \). According to Theorem 1.5.2.3.c in [16], to prove that \(\partial _{\nu _{{A^*}}}\phi _g\in H^{1/2}(\varGamma _j\cup \varGamma _{j+1})\), we have to show that
First notice that \(\Vert \phi _g\Vert _{H^2(\varOmega )}\le C\Vert g\Vert _{L^2(\varOmega )}\). Since \(\phi _g\in H^2(\varOmega )\), then \(\nabla \phi _g\in (H^1(\varOmega ))^2\), and the usual trace theorem says that \(\partial _i \phi _g\in H^{1/2}(\varGamma )\) for \(i=1,2\). As is shown in the first part of the proof of Theorem 1.5.2.3.c) in [16], this implies that
for \(i=1,2\). We are going to transform the integral in (41) into a combinations of integrals involving the partial derivatives. To do that, without loss of generality, we can suppose that \(\varGamma _j\) is on the negative part of the x axis, \(S_j\) is at the origin and \(\varGamma _{j+1}\subset \{ (-\sigma \,n_2,\sigma \,n_1)\mid \ 0\le \sigma \}\), so that the normal and tangent vectors to \(\varGamma _j\) and \(\varGamma _{j+1}\) respectively are \(\nu _j=(0,-1)^T\), \(\tau _j=(1,0)^T\) and \(\nu _{j+1}=(n_1,n_2)^T\), \(\tau _{j+1}=(-n_2,n_1)^T\) where \(n_1>0\) and \(n_1^2+n_2^2=1\). The functions \(r,s,\gamma _1,\gamma _2\in C^{0,1}(\varGamma _j\cup \varGamma _{j+1})\) defined as
satisfy that
where \({\mathcal {A}}^T\) is the transpose matrix of
Therefore, we have
Since \(\phi _g=0\) on \(\varGamma \), the tangential derivatives in that expression are zero. Therefore, we only have to prove for \(i=1,2\) that
To prove this, we first insert the term \(\gamma _i (x_j(\sigma )) \partial _{i}\phi _g(x_j(-\sigma ))\) and apply Young’s inequality. Next we apply the fundamental theorem of Calculus and take advantage of the Lipschitz regularity of \(\gamma _i\) to obtain
which is finite thanks to (42) and the fact that the trace of \(\partial _{i}\phi _g\) is in \(H^{1/2}(\varGamma )\hookrightarrow L^2(\varGamma ).\)
Making the same analysis for each corner, we have proved the claimed regularity.
Rights and permissions
About this article
Cite this article
Mateos, M. Sparse Dirichlet optimal control problems. Comput Optim Appl 80, 271–300 (2021). https://doi.org/10.1007/s10589-021-00290-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-021-00290-7