Abstract
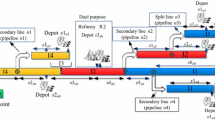
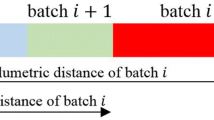
Brazilian petrobras is one of the world largest oil companies. Recurrently, it faces a very difficult planning and scheduling problem: how to operate a large pipeline network in order to adequately transport oil derivatives and biofuels from refineries to local markets. In spite of being more economical and environmentally safer, the use of a complex pipeline network poses serious operational difficulties related to resource allocation and temporal constraints. The current approaches known from the literature only consider a few types of constraints and restricted topologies, hence they are far from being applicable to real instances from petrobras. We propose a hybrid framework based on a two-phase problem decomposition strategy. A novel Constraint Programming (CP) model plays a key role in modelling operational constraints that are usually overlooked in literature, but that are essential in order to guarantee viable solutions. The full strategy was implemented and produced very adequate results when tested over large real instances.
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
5th International Planning Competition (2006). http://zeus.ing.unibs.it/ipc-5/.
Alves, V., & Filho, V. J. (2007). Pipeline scheduling of petroleum derivatives using genetic algorithm. In IV Congresso Brasileiro de Pesquisa e Desenvolvimento em Petróleo e Gás. Campinas, Brazil.
Cafaro, D. C., & Cerdá, J. (2004). Optimal scheduling of multiproduct pipeline systems using a non-discrete MILP formulation. Computers & Chemical Engineering, 28(10), 2053–2058.
Camponogara, E. (1995). A-Teams para um problema de transporte de derivados de petróleo. Master’s thesis, Instituto de Matemática, Estatística e Ciência da Computação, Universidade Estadual de Campinas, Campinas, Brazil. In Portuguese.
Camponogara, E., & Souza, P. S. (1996). A-Teams for oil transportation problem through pipelines. In Information systems analysis and synthesis. Orlando, United States.
Cheng, B. M. W., Choi, K. M. F., Lee, J. H. M., & Wu, J. C. K. (1999). Increasing constraint propagation by redundant modeling: An experience report. Constraints, 4(2), 167–192. citeseer.ist.psu.edu/cheng99increasing.html.
Crane, D. S., Wainwright, R. L., & Schoenefeld, D. A. (1999). Scheduling of multi-product fungible liquid pipelines using genetic algorithms. In Proceedings of the 1999 ACM symposium on applied computing (pp. 280–285). San Antonio, USA.
de la Cruz, J., Andrés-Toro, B., Herrán-González, A., Porta, E. B., & Blanco, P.F. (2003). Multiobjective optimization of the transport in oil pipelines networks. In Proceedings of the IEEE conference on emerging technologies and factory automation (Vol. 1, pp. 566–573).
de la Cruz, J., Herrán-González, A., Risco-Martín, J., & Andrés-Toro, B. (2005). Hybrid heuristic and mathematical programming in oil pipelines networks: Use of immigrants. Journal of Zhejiang University Science, 6A(1), 9–19.
Filho, E. M. S., Filho, V. J., & de Lima, L. S. (2007). Variable neighborhood search (VNS) applied to pipeline distribution problem with capacity constraints. In IV Congresso Brasileiro de Pesquisa e Desenvolvimento em Petróleo e Gás. Campinas, Brazil.
Group, A. E. (2001). How pipelines make the oil market work—their networks, operation and regulation. New York: Association of Oil Pipe Lines.
Hooker, J. N. (2006). Integrated methods for optimization (International series in operations research & management science). Secaucus: Springer.
ILOG (2006). ILOG scheduler 6.2: User’s manual. ILOG.
Kautz, H., Horvitz, E., Ruan, Y., Gomes, C., & Selman, B. (2002). Dynamic restarts policies. In Proceedings of the AAAI-2002. Edmonton, Alberta.
Magatao, L., Arruda, L., & Neves, F. (2004). A mixed integer programming approach for scheduling commodities in a pipeline. Computers & Chemical Engineering, 28(1), 171–185.
Magatao, L., Arruda, L., & Neves, F. (2005). Using CLP and MILP for scheduling commodities in a pipeline. Computer-Aided Chemical Engineering, 20B, 1027–1032.
Marriot, K., & Stuckey, P. (1998). Programming with constraints: An introduction (1st ed.). Cambridge: MIT.
Milidíu, R., & dos Santos Liporace, F. (2003). Planning of pipeline oil transportation with interface restrictions is a difficult problem. Tech. rep. 56, Departamento de Informática, PUC-Rio, Rio de Janeiro, RJ, Brasil.
Milidíu, R., dos Santos Liporace, F., & de Lucena, C. J. P. (2003). Pipesworld: Planning pipeline transportation of petroleum derivatives. In Proceedings of ICAPS’03—Workshop on the competition: Impact, organization, evaluation, benchmarks. Trento, Italy.
Milidiú, R. L., Pessoa, A. A., & Laber, E. S. (2002). Pipeline transportation of petroleum products with no due dates. In LATIN ’02: Proc. of the 5th Latin American symposium on theoretical informatics (pp. 248–262). London: Springer.
Milidiú, R. L., Pessoa, A. A., & Laber, E. S. (2003). The complexity of makespan minimization for pipeline transportation. Theoretical Computer Science, 306(1–3), 339–351. doi:10.1016/S0304-3975(03)00291-3.
Moura, A., de Souza, C., Cire, A., & Lopes, T. (2008). Heuristics and constraint programming hybridizations for a real pipeline planning and scheduling problem. In Proceedings of the 11th IEEE international conference on computational science and engineering—CSE’08 (pp. 455–462).
Moura, A., de Souza, C., Cire, A., & Lopes, T. (2008). Planning and scheduling the operation of a very large oil pipeline network. In Lecture notes in computer science—proceedings of the 14th international conference on principles and practice of constraint programming (Vol. 5202, pp. 36–51).
Rejowski, R., & Pinto, J. M. (2003). Scheduling of a multiproduct pipeline system. Computers & Chemical Engineering, 27(8), 1229–1246.
Rejowski, R., & Pinto, J. M. (2004). Efficient MILP formulations and valid cuts for multiproduct pipeline scheduling. Computers & Chemical Engineering, 28(8), 1511–1528.
Rejowski, R., & Pinto, J. M. (2008). A novel continuous time representation for the scheduling of pipeline systems with pumping yield rate constraints. Computers & Chemical Engineering, 32, 1042–1066.
Relvas, S., Barbosa-Póvoa, A. P. F. D., Matos, H. A., Fialho, J., & Pinheiro, A. S. (2006). Pipeline scheduling and distribution centre management—A real-world scenario at CLC. In Proceedings of the 16th European symposium on computer aided process engineering and 9th international symposium on process systems engineering (pp. 2135–2140). Garmisch-Partenkirchen, Germany.
Relvas, S., Matos, H. A., Barbosa-Póvoa, A. P. F. D., Fialho, J., & Pinheiro, A. S. (2006). Pipeline scheduling and inventory management of a multiproduct distribution oil system. Industrial & Engineering Chemistry Research, 45(23), 7841–7855.
Relvas, S., Matos, H. A., Barbosa-Póvoa, A. P. F. D., & Fialho, J. (2007). Reactive scheduling framework for a multiproduct pipeline with inventory management. Industrial & Engineering Chemistry Research, 46(17), 5659–5672.
Sasikumar, M., Prakash, P. R., Patil, S. M., & Ramani, S. (1997). Pipes: A heuristic search model for pipeline schedule generation. Knowledge-Based Systems, 10(3), 169–175.
Wilson, R. (2001). Transportation in America (18th ed.). Washington, D.C.: Eno Transportation Foundation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lopes, T.M.T., Ciré, A.A., de Souza, C.C. et al. A hybrid model for a multiproduct pipeline planning and scheduling problem. Constraints 15, 151–189 (2010). https://doi.org/10.1007/s10601-009-9086-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10601-009-9086-z