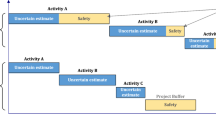
Abstract
An important component in critical chain project management is a scheduling methodology to support resource constraints. Given task duration estimates and precedence relations along with resource designation for each task, one seeks to adhere to a target due date as well as to shorten the estimated makespan. Key are two types of time buffers to absorb potential delays accumulated from preceding tasks, and this makes the problem complex and hard to solve. The “good enough” strategy has been prevalent in research, focusing on the development of heuristic solution methods. There has been only one attempt to minimize estimated makespan, wherein discrete algebra is utilized. The method is, however, inflexible as you must compose a search space. Even the slightest extension requires a major recast of the approach. Hence, we develop a new approach to find an exact optimal solution in an efficient manner. Given a project instance, an optimization problem is constructed as a mixed-integer linear-program, for which an exact solution can be found using an off-the-shelf solver. While the problem is NP hard, larger-scale project instances, including up to 30 tasks, can be solved within a practical time standard. Extension with respect to resource assignment is easily accomplished. Experimental results highlight the significance of the developed framework.





Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Goldratt, E. M. (1997). Critical chain. Great Barrington: North River Press.
Leach, L. P. (2004) Critical chain project management: Effective project management series, 2nd edn. Boston: Artech House.
Wei, B., & Ying, D. F. (2013). Selecting service suppliers in construction supply chains with a critical chain model. Applied Mechanics and Materials, 411-414, 2645–2650. https://doi.org/10.4028/www.scientific.net/AMM.411-414.2645.
Dong, L., Zhao, X. K., Zhou, W. P., & Lv, Q. (2013). Application of critical chain project scheduling theory in power plant electrical equipment maintenance. Advanced Materials Research, 614-615, 1985–1989. https://doi.org/10.4028/www.scientific.net/AMR.614-615.1985.
Hutanu, A., Prostean, G., & Badea, A. (2015). Integrating critical chain method with AGILE life cycles in the automotive industry. Procedia - Social and Behavioral Sciences, 197, 1416–1421. https://doi.org/10.1016/j.sbspro.2015.07.088.
Newbold, R. C. (1998). Project Management in the fast lane: Applying the theory of constraints. Boca Raton: CRC Press.
Ghaffari, M., & Emsley, M. W. (2015). Current status and future potential of the research on critical chain Project Management. Surveys in Operations Research and Management Science, 20(2), 43–54. https://doi.org/10.1016/j.sorms.2015.10.001.
Peng, W. L., & Xu, H. (2012). The scheduling problem of active critical chain method. Information Technology Journal, 11(7), 829–839. https://doi.org/10.3923/itj.2012.829.839.
Herroelen, W., & Leus, R. (2001). On the merits and pitfalls of critical chain scheduling. Journal of Operations Management, 19(5), 559–577. https://doi.org/10.1016/S0272-6963(01)00054-7.
Tukel, O. I., Rom, W. O., & Eksioglu, S. D. (2006). An investigation of buffer sizing techniques in critical chain scheduling. European Journal of Operational Research, 172(2), 401–416. https://doi.org/10.1016/j.ejor.2004.10.019.
Gao, P., Feng, J., & Wang, H. (2007). Grey critical chain project scheduling technique and its application. Canadian Social Science, 3(3), 35–41. https://doi.org/10.3968/j.css.1923669720070303.005.
Long, L. D., & Ohsato, A. (2008). Fuzzy critical chain method for project scheduling under resource constraints and uncertainty. International Journal of Project Management, 26(6), 688–698. https://doi.org/10.1016/j.ijproman.2007.09.012.
Zhao, Z. Y., You, W. Y., & Zuo, J. (2010). Application of innovative critical chain method for project planning and control under resource constraints and uncertainty. Journal of Construction Engineering and Management, 136(9), 1056–1060. https://doi.org/10.1061/(ASCE)CO.1943-7862.0000209.
Pawiński, G., & Sapiecha, K. (2012). Resource allocation optimization in critical chain method. Annales UMCS Informatica Sectio AI XII, 12, 17–29. https://doi.org/10.2478/v10065-012-0006-2.
Peng, W., Su, H., & Hao, Y. (2013). A Genetic Algorithm for The Critical Chain Project Scheduling Problem. International Journal of Digital Content Technology and its Applications, 7(3), 571–577. https://doi.org/10.4156/jdcta.vol7.issue3.71.
Peng, W., & Huang, M. (2013). A critical chain project scheduling method based on a differential evolution algorithm. International Journal of Production Research, 52(13), 3940–3949. https://doi.org/10.1080/00207543.2013.865091.
Wang, W.-x., Wang, X., X-l, G., & Deng, L. (2014). Multi-objective optimization model for multi-project scheduling on critical chain. Advances in Engineering Software, 68, 33–39. https://doi.org/10.1016/j.advengsoft.2013.11.004.
Goto, H., & Murray, A. T. (2018). Optimization of project schedules in the critical-chain project-management max-plus-linear framework. International review on Modelling and simulations, 11(4), 206–214. https://doi.org/10.15866/iremos.v11i4.13485.
Heidergott, B., Olsder, G. J., & van der Woude, J. (2006). Max plus at work: Modeling and analysis of synchronized systems. Princeton series in applied mathematics. New Jersey: Princeton University Press.
Grossmann, I. E. (2002). Review of nonlinear mixed-integer and disjunctive programming techniques. Optimization and Engineering, 3(3), 227–252. https://doi.org/10.1023/a:1021039126272.
Goto, H., & Murray, A. T. (2019). Small-m method for detecting all longest paths. OPSEARCH, 56(3), 824–839. https://doi.org/10.1007/s12597-019-00385-0.
Kolisch, R., Sprecher, A., & Drexl, A. (1995). Characterization and generation of a general class of resource-constrained project scheduling problems. Management Science, 41(10), 1693–1703. https://doi.org/10.1287/mnsc.41.10.1693.
Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers JP18K01126 and JP18K04628.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Goto, H., Murray, A.T. Exact and flexible solution approach to a critical chain project management problem. Constraints 25, 280–297 (2020). https://doi.org/10.1007/s10601-020-09314-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10601-020-09314-1