Abstract
In many real applications such as virtual metrology in semiconductor manufacturing, face recognition, and gait recognition in computer vision, the input data is naturally expressed as tensors or multi-dimensional arrays. Furthermore, in addition to the known label information, domain knowledge can often be obtained from various sources, e.g., multiple domain experts. To address such problems, in this paper, we propose a general optimization framework for dealing with tensor inputs while taking into consideration domain knowledge. To be specific, our framework is based on a linear model, and we obtain the weight tensor in a hierarchical way—first approximate it by a low-rank tensor, and then estimate the low-rank approximation using the domain knowledge from various sources. This is motivated by wafer quality prediction in semiconductor manufacturing. We also propose an effective algorithm named H-MOTE for solving this framework, which is guaranteed to converge. For each iteration, the time complexity of H-MOTE is linear with respect to the number of examples as well as the size of the weight tensor. Therefore, H-MOTE is scalable to large-scale problems. Experimental results show that H-MOTE outperforms state-of-the-art techniques on both synthetic and real data sets.











Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
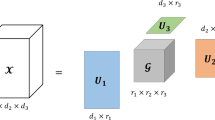
Note that the vectorized version of the tensor may not be unique due to different orderings of the fibers.
The results of the the other two methods are similar as in Fig. 1.
Currently we are trying to address the challenge of different duration for different steps, so that the input tensors contain instantaneous measurements, which may improve the performance of quality prediction.
We omit the name of the variable due to confidential issues.
References
Bishop CM (2006) Pattern recognition and machine learning (Information Science and Statistics). Springer, Secaucus
Cai D, He X, Han J (2006) Learning with tensor representation. Technical Report. University of Illinois at Urbana, Champaign
Chang Y-J, Kang Y, Hsu C-L, Chang C-T, Chan TY (2006) Virtual metrology technique for semiconductor manufacturing. In: IJCNN
Dai G, Yeung D-Y (2006) Tensor embedding methods. In: AAAI
Grippo L, Sciandrone M (2000) On the convergence of the block nonlinear Gauss–Seidel method under convex constraints. Oper Res Lett 26(3):127–136
He X, Cai D, Niyogi P (2005) Tensor subspace analysis. MIT Press, In: NIPS
Hochreiter S, Obermayer K (2004) Classification, regression, and feature selection on matrix data. Technical Report. Technische Universitat, Berlin
Kang P, Kim D, Lee H-J, Doh S, Cho S (2011) Virtual metrology for run-to-run control in semiconductor manufacturing. Expert Syst Appl 38:2508–2522
Khan AA, Moyne JR, tilbury DM (2008) Virtual metrology and feedback control for semiconductor manufacturing processes using recursive partial least squares. J Process Control 18:961–974
Kolda TG, Bader BW (2009) Tensor decompositions and applications. SIAM Rev 51(3):455–500
Li X, Lin S, Yan S, Xu D (2008) Discriminant locally linear embedding with high-order tensor data. IEEE Trans Syst Man Cybern 38(2):342–352
Lynn S, Ringwood J, Ragnoli E, McLoone S, MacGearailt N (2009) Virtual metrology for plasma etch using tool variables. In: Advanced Semiconductor Manufacturing Conference
Mitchell TM (1997) Machine Learning. McGraw-Hill, New York
Platt JC (1999) Advances in kernel methods. MIT Press, Cambridge, MA.
Roweis ST, Saul LK (2000) Nonlinear dimensionality reduction by locally linear embedding. SCIENCE 290:2323–2326
Su Y-C, Lin T-H, Cheng F-T, Wu W-M (2008) Accuracy and real-time considerations for implementing various virtual metrology algorithms. IEEE Trans Semicond Manuf 21(3):426–434
Sun J, Tao D, Papadimitriou S, Yu PS, Faloutsos C (2008) Incremental tensor analysis: Theory and applications. TKDD 2(3):11
Tao D, Li X, Hu W, Maybank S, Wu X (2005) Supervised tensor learning. In: ICDM, IEEE Computer Society, pp. 450–457
Tao D, Li X, Maybank SJ, Wu X (2006) Human carrying status in visual surveillance. In: CVPR, pp. 1670–1677
Tao D, Li X, Wu X, Maybank SJ (2007) General tensor discriminant analysis and gabor features for gait recognition. IEEE Trans Pattern Anal Mach Intell 29(10):1700–1715
Tao D, Sun J, Shen J, Wu X, Li X, Maybank SJ, Faloutsos C (2008) Bayesian tensor analysis. In: IJCNN, pp. 1402–1409
Vapnik VN (2000) The nature of statistical learning theory. Springer, New York
Wang Q, Chen F, Xu W (2011) Tracking by third-order tensor representation. IEEE Trans Syst Man Cybern 41:385–396
Wasserman L (2009) All of statistics. Springer, New York
Zhu Y, He J, Lawrence RD (2012) Hierarchical modeling with tensor inputs. In: AAAI Conference on Artificial Intelligence, pp. 1233–1239
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editor: Chih-Jen Lin.
Rights and permissions
About this article
Cite this article
Zhu, Y., He, J. & Lawrence, R.D. A general framework for predictive tensor modeling with domain knowledge. Data Min Knowl Disc 29, 1709–1732 (2015). https://doi.org/10.1007/s10618-014-0392-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10618-014-0392-8