Abstract
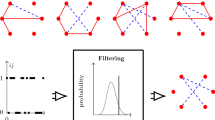
Vertices with high betweenness and closeness centrality represent influential entities in a network. An important problem for time varying networks is to know a-priori, using minimal computation, whether the influential vertices of the current time step will retain their high centrality, in the future time steps, as the network evolves. In this paper, based on empirical evidences from several large real world time varying networks, we discover a certain class of networks where the highly central vertices are part of the innermost core of the network and this property is maintained over time. As a key contribution of this work, we propose novel heuristics to identify these networks in an optimal fashion and also develop a two-step algorithm for predicting high centrality vertices. Consequently, we show for the first time that for such networks, expensive shortest path computations in each time step as the network changes can be completely avoided; instead we can use time series models (e.g., ARIMA as used here) to predict the overlap between the high centrality vertices in the current time step to the ones in the future time steps. Moreover, once the new network is available in time, we can find the high centrality vertices in the top core simply based on their high degree. To measure the effectiveness of our framework, we perform prediction task on a large set of diverse time-varying networks. We obtain F1-scores as high as 0.81 and 0.72 in predicting the top m closeness and betweenness centrality vertices respectively for real networks where the highly central vertices mostly reside in the innermost core. For synthetic networks that conform to this property we achieve F1-scores of 0.94 and 0.92 for closeness and betweenness respectively. We validate our results by showing that the practical effects of our predicted vertices match the effects of the actual high centrality vertices. Finally, we also provide a formal sketch demonstrating why our method works.






Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
In this paper, when we mention highly central vertices, we specifically refer to high closeness or betweenness centrality and not other types of centralities.
We tried with other stretches of size 15, 25 etc. The results do not seem to be affected by such minor variations. Ideally this size should not be too large thus consuming a lot of data for prediction, nor it should be too small thus having too few points to correctly predict. Through experimentation, we find that a size close to 20 strikes an ideal balance.
Note that if we keep increasing the number of top vertices, the prediction results can only get better. Through experiments, we observe that small numbers like 5 and 10 are judicial choices.
References
Agneessens F, Borgatti SP, Everett MG (2017) Geodesic based centrality: unifying the local and the global. Soc Netw 49:12–26
Alvarez-Hamelin JI, Dall’Asta L, Barrat A, Vespignani A (2006) Large scale networks fingerprinting and visualization using the k-core decomposition. In: Advances in neural information processing systems (NIPS), pp 41–50
Baeza-Yates R, Ribeiro-Neto B et al (1999) Modern information retrieval, vol 463. ACM Press, New York
Barucca P, Tantari D, Lillo F (2016) Centrality metrics and localization in core-periphery networks. J Stat Mech Theory Exp 2016(2):023401
Batagelj V, Zaversnik M (2003) An o(m) algorithm for cores decomposition of networks. arXiv preprint arXiv:cs.DS/0310049
Benyahia O, Largeron C, Jeudy B, Zaïane OR (2016) Dancer: dynamic attributed network with community structure generator. In: Joint European conference on machine learning and knowledge discovery in databases. Springer, pp 41–44
Borgatti SP, Carley KM, Krackhardt D (2006) On the robustness of centrality measures under conditions of imperfect data. Soc Netw 28(2):124–136
Box GE, Jenkins GM, Reinsel GC, Ljung GM (2015) Time series analysis: forecasting and control. Wiley, Hoboken
Braha D, Bar-Yam Y (2006) From centrality to temporary fame: dynamic centrality in complex networks. Complexity 12(2):59–63
Braha D, Bar-Yam Y (2009) Time-dependent complex networks: dynamic centrality, dynamic motifs, and cycles of social interactions. In: Gross T, Sayama H (eds) Adaptive networks: theory, models and applications. Springer studies on complexity. Springer, Berlin, pp 39–50
Carnes T, Nagarajan C, Wild SM, Van Zuylen A (2007) Maximizing influence in a competitive social network: a follower’s perspective. In: Proceedings of the 9th international conference on electronic commerce. ACM, pp 351–360
Freeman LC (1978) Centrality in social networks conceptual clarification. Soc Netw 1(3):215–239
Govindan P, Soundarajan S, Eliassi-Rad T, Faloutsos C (2016) Nimblecore: a space-efficient external memory algorithm for estimating core numbers. In: IEEE/ACM international conference on advances in social networks analysis and mining (ASONAM), 2016. IEEE, pp 207–214
Gutfraind A, Safro I, Meyers LA (2015) Multiscale network generation. In: 18th international conference on information fusion (FUSION), 2015. IEEE, pp 158–165
Hamilton JD (1989) A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57:357–384
Hempel S, Koseska A, Kurths J, Nikoloski Z (2011) Inner composition alignment for inferring directed networks from short time series. Phys Rev Lett 107(5):054101
Hill SA, Braha D (2010) Dynamic model of time-dependent complex networks. Phys Rev E 82(4):046105
Holme P (2015) Modern temporal network theory: a colloquium. Euro Phys J B 88(9):1–30
Holme P, Saramäki J (2012) Temporal networks. Phys Rep 519(3):97–125
Khaouid W, Barsky M, Srinivasan V, Thomo A (2015) K-core decomposition of large networks on a single PC. Proc VLDB Endow 9(1):13–23
Kim H, Anderson R (2012) Temporal node centrality in complex networks. Phys Rev E 85(2):026107
Kim H, Tang J, Anderson R, Mascolo C (2012) Centrality prediction in dynamic human contact networks. Comput Netw 56(3):983–996
Kitsak M, Gallos LK, Havlin S, Liljeros F, Muchnik L, Stanley HE, Makse HA (2010) Identification of influential spreaders in complex networks. Nat Phys 6(11):888–893
Kunegis J (2013) Konect: the Koblenz network collection. In: Proceedings of the 22nd international conference on world wide web (WWW). ACM, pp 1343–1350
Lerman K, Ghosh R, Kang JH (2010) Centrality metric for dynamic networks. In: Proceedings of the 8th workshop on mining and learning with graphs. ACM, pp 70–77
Leskovec J, Krevl A (2014) SNAP datasets: Stanford large network dataset collection. http://snap.stanford.edu/data. Accessed Jan 2016
Liu HL, Ma C, Xiang BB, Tang M, Zhang HF (2018) Identifying multiple influential spreaders based on generalized closeness centrality. Phys A 492:2237–2248
Morselli C, Masias VH, Crespo F, Laengle S (2013) Predicting sentencing outcomes with centrality measures. Secur Inf 2(1):4
Nicosia V, Tang J, Mascolo C, Musolesi M, Russo G, Latora V (2013) Graph metrics for temporal networks. In: Holme P, Saramäki J (eds) Temporal networks, understanding complex systems. Springer, Berlin, pp 15–40
OBrien MP, Sullivan BD (2014) Locally estimating core numbers. In: IEEE international conference on data mining (ICDM), 2014. IEEE, pp 460–469
Peng C, Kolda TG, Pinar A (2014) Accelerating community detection by using k-core subgraphs. arXiv preprint arXiv:1403.2226
Rozenshtein P, Gionis A (2016) Temporal pagerank. In: Joint European conference on machine learning and knowledge discovery in databases. Springer, pp 674–689
Scherrer A, Borgnat P, Fleury E, Guillaume JL, Robardet C (2008) Description and simulation of dynamic mobility networks. Comput Netw 52(15):2842–2858
Seidman SB (1983) Network structure and minimum degree. Soc Netw 5(3):269–287
Sikdar S, Ganguly N, Mukherjee A (2016) Time series analysis of temporal networks. Euro Phys J B 89(1):1–11
Taylor D, Myers SA, Clauset A, Porter MA, Mucha PJ (2015) Eigenvector-based centrality measures for temporal networks. arXiv preprint arXiv:1507.01266
Ufimtsev V, Sarkar S, Mukherjee A, Bhowmick S (2016) Understanding stability of noisy networks through centrality measures and local connections. In: Proceedings of the 25th ACM international on conference on information and knowledge management (CIKM). ACM, pp 2347–2352
Yang Y, Dong Y, Chawla NV (2014) Predicting node degree centrality with the node prominence profile. Sci Rep 4:7236
Zhou H, Xu S, Huang C (2015) Temporal centrality prediction in opportunistic mobile social networks. In: International conference on internet of vehicles. Springer, pp 68–77
Zhou H, Leung VC, Zhu C, Xu S, Fan J (2017) Predicting temporal social contact patterns for data forwarding in opportunistic mobile networks. IEEE Trans Veh Technol 66(11):10372–10383
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editors: Jesse Davis, Elisa Fromont, Derek Greene, Björn Bringmann.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Sarkar, S., Sikdar, S., Bhowmick, S. et al. Using core-periphery structure to predict high centrality nodes in time-varying networks. Data Min Knowl Disc 32, 1368–1396 (2018). https://doi.org/10.1007/s10618-018-0574-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10618-018-0574-x