1 Introduction

In data mining, several analysis tasks are used to extract useful and hidden information from raw data. One of the most important tasks is anomaly detection which is crucial to many real applications. Identifying anomalous instances in a dataset can lead to discovering patterns that do not match the most common patterns of the data; this has many critical applications that have been widely addressed in the literature. To illustrate: in the context of healthcare (Christy et al. 2015), it is critical to find abnormal heart activity or medical diagnosis (Schlegl et al. 2017); in information systems security (Kuna et al. 2014; Iglesias and Zseby 2015), it is essential to detect intrusions or anomalous activity patterns in web services; in public services management (Kaddour and Lehsaini 2021), it helps identifying abnormal energy consumption; in finance (Ngai et al. 2011), it is critical to detect fraud and anomalous credit card transactions; in social networks (Yu et al. 2017; Schubert et al. 2015a), it is essential to find out which anomalous events are trending and monitor their evolution; in urban traffic data (Djenouri and Zimek 2018), observed anomalies can hint at accidents or other problems in the urban traffic network. Anomaly detection, or outlier detection, is important because it provides meaningful, often crucial, actionable information for a wide variety of application domains.

Grubbs (1969) proposed one of the first definitions of an outlier in the statistical literature: “An outlying observation, or ‘outlier’, appears to deviate markedly from other members of the sample in which it occurs”. Another well-known definition proposed by Hawkins (1980) presents an outlier as “An observation which deviates so much from another observations as to arouse suspicions that it was generated by a different mechanism”. Barnett et al. (1994) define an outlier as “An observation (or subset of observations) which appears to be inconsistent with the remainder of that set of data”. If we summarize all these classic definitions, there are two common factor: the rarity of the anomalous instance and the meaning underlying its presence in the data. Based on the fact that there is no unambiguous definition of what is an outlier precisely, each method relies on an approach based on certain assumptions of what qualifies to be an anomaly. Hence, the nature of the data often determines the applicability of each approach.

Various methods proposed in the literature can be categorized as follows. Statistical methods identify outliers depending on their relationship to the distribution model that is assumed to generate the data (Yang et al. 2009; Tang et al. 2015). Graph-based methods capture the interdependence of instances represented by nodes in a graph to find outliers (Moonesinghe and Tan 2008; Wang et al. 2018). Learning-based methods leverage deep learning, active learning, or other supervised learning techniques to identify outliers (Abe et al. 2006; Görnitz et al. 2013; Chalapathy and Chawla 2019; Pang et al. 2022; Marques et al. 2023). Distance-based methods consider an instance an outlier if it is far from its nearest neighbors (Knorr and Ng 1998; Ramaswamy et al. 2000; Angiulli et al. 2005; Orair et al. 2010). Density-based methods assume that an outlier must occur in a low-density region of the data space (Breunig et al. 2000; Tang et al. 2002; Papadimitriou et al. 2003). Ensemble methods combine results from different models to produce more robust meta-models that effectively spot outliers (Zimek et al. 2014; Rayana and Akoglu 2016). Finally, clustering-based methods – the focus of our study, as these have so-far been neglected in literature – detect outliers by capitalizing on the results of a clustering algorithm. A cluster is often understood as one partition or subset of the dataset that does not overlap with any other cluster (MacQueen 1967). Clustering-based methods for outlier detection generally assume that anomalies do not belong to any cluster, or are forced to be in a cluster with remarkably different other instances, or even belong to tiny clusters (Jiang et al. 2001).

1.1 Why clustering-based outlier detection?

When reviewing existing surveys and comparative studies on outlier detection (Sect. 2), we will see that clustering-based methods have been mostly ignored or overlooked in previous studies. We advocate that more engagement is needed from the data mining community in performing extensive assessments of the true capabilities of clustering-based outlier detection approaches.

One might expect nowadays deep learning methods to excel also in outlier detection. However, a recent study (Han et al. 2022) found that several classic, simple, unsupervised methods outperformed many deep-learning-based supervised methods. We therefore take the best classic unsupervised (but not clustering-based: nearest-neighbor outlier detection, the local outlier factor, LOF, and isolation forests) methods as baselines here. As opposed to deep-learning-based methods, these are fast and efficient and do not require training and much less hyper-parameter tuning.

While the classic, unsupervised methods do not use a clustering structure explicitly, many of them assume implicitly that there is some clustering structure in the data, and they identify outliers as those observations that would not belong (to some degree) to such implicit clusters (Zimek and Filzmoser 2018). It is noteworthy that outlier detection and clustering also often occur as a two-fold application of the same underlying techniques, as, e.g., in LOF (Breunig et al. 2000) and OPTICS (Ankerst et al. 1999), GLOSH and HDBSCAN* (Campello et al. 2015), or Sparse Data Observers for outlier detection (Iglesias Vázquez et al. 2018) and for clustering (Iglesias et al. 2023) (here, interestingly, the technique was developed first for outlier detection and then adjusted to clustering). It should therefore be interesting to see if making the cluster-assumption explicit would change the quality of results in any way. As we will see, clustering-based methods are generally on par with the classic unsupervised state-of-the-art methods.

It can be efficient and more robust against different notions of clusterings to not model clusterings explicitly, yet making the clustering explicit can also have several benefits:

  • Unsupervised evaluation measures are more mature for clustering than for outlier detection, and it might be possible to make progress in the unsupervised evaluation of outliers from this perspective;

  • (Subspace) Clustering in high-dimensional data is more developed than (subspace) outlier detection, and it could thus be a promising direction to approach (subspace) outlier detection in high-dimensional data from the clustering perspective;

  • Clustering on streaming data is more developed and robust than outlier detection, thus interesting stream outlier detection methods could be developed based on clustering methods;

  • Clustering-based methods for outlier detection would offer alternative possibilities for efficiency improvements, as many clustering methods have been improved a lot in terms of runtime over the years, offering alternatives to the typical filter-refinement-approaches used for (top-n) outlier detection;

  • Making clusterings explicit seems also to be a promising directions towards explainable outlier detection.

We will elaborate more on these aspects for future research in the outlook (Sect. 7.2), but already here these perspectives shall motivate why looking at clustering-based methods for outlier detection should be interesting, especially if they are not better or worse than the classic state-of-the-art methods.

1.2 Contributions

It is essential to conduct evaluations that encompass both effectiveness and efficiency, considering various types of data and the most representative methods of this approach. Our work addresses this challenge by examining the use of such techniques in diverse scenarios and evaluating their advantages and disadvantages in comparison with one another, as well as with established non-clustering-based methods. We present the initial endeavor as a comprehensive experimental evaluation of clustering-based outlier detection methods, encompassing a diverse collection of real and synthetic datasets and numerous parameter configurations. We employ well-known measures for evaluating outlier detection effectiveness on each dataset. Furthermore, we conduct a comparative analysis of different categories of clustering-based outlier detection methods, each representing a distinct underlying approach to outlier detection. Additionally, we devise one heuristic for parameterization that ensures similar parameter values are considered for methods within the same category, enabling us to compare the relative behavior of the methods within and across categories.

In summary, our main contributions are:

  • C1 Accuracy evaluation We perform a comparative statistical analysis of 11 unsupervised clustering-based outlier detectors in terms of accuracy, including also 3 selected established non-clustering-based methods.

  • C2 Resilience to data variation evaluation We conduct an extensive experimental study of the resilience of the methods when analyzing data of distinct nature, considering 23 real and 23 synthetic datasets.

  • C3 Resilience to parameter variation evaluation We conduct an extensive experimental study of the resilience of the methods to variation in their parameter configuration.

  • C4 Automatized parameter selection evaluation We analyze the feasibility of filtering out parameter values inappropriate to outlier detectors automatically, based on internal measures of clustering quality.

  • C5 Scalability evaluation We analyze the scalability of outlier detectors on datasets with different dimensionality and different number of clusters to provide experimental evidence that help selecting a method based on its efficiency in handling large datasets.

The rest of the paper follows a traditional organization. We begin by discussing the related work (Sect. 2) and introducing the anomaly detection methods used in our study (Sect. 3). Next, we describe the selection and design of data sets (real and synthetic), explain the parameter configuration and the evaluation measures used (Sect. 4), and then summarize and discuss the results obtained (Sect. 5). Finally, we conclude the paper with an overview and discussion of our findings (Sect. 6) and interesting topics for future work (Sect. 7).

1.3 Reproducibility

To foster future work on the clustering-based approach for outlier detection and for reproducibility, all the data and code used in our experiments are freely available online, at https://github.com/BraulioSanchez/clustering-based-outlier-detection.

2 Related work

Many surveys and some comparative evaluation studies are available in the literature. Here we can only highlight the more closely related examples.

Hodge and Austin (2004) conducted a comparative analysis of anomaly detection algorithms published at that time, where they identified the underlying assumptions of each algorithm and highlighted their respective advantages and disadvantages. They categorized anomaly detection into three fundamental approaches: unsupervised clustering, supervised classification, and novelty detection (semi-supervised). The authors recommend selecting an appropriate anomaly detection algorithm based on the attributes involved and the distribution model, considering the algorithm’s ability to handle new data points as they arrive incrementally. Additionally, they suggest considering which of the three fundamental approaches is most suitable for solving the specific problem in each application. For unsupervised clustering approaches, the authors presented k-NN, k-means, and k-medoids, along with their optimized variations, as strategies for identifying sparse regions in the dataset where anomalous points are more likely to occur. Furthermore, the authors mention three clustering algorithms, CLARANS (Ng and Han 1994), BIRCH (Zhang et al. 1996), and DBSCAN (Ester et al. 1996), as representative data mining algorithms. These algorithms exhibit robustness, allowing them to tolerate the presence of outliers in the dataset while enabling anomaly detection as a by-product of the clustering process. Unlike our study, Hodge and Austin’s research did not include experimental evaluations of the algorithms analyzed and did not extensively explore unsupervised clustering approaches, which is the primary motivation behind our work.

Chandola et al. (2009) grouped the existing anomaly detection techniques into six categories, identifying the base assumption that defines each approach and the different techniques that exist per approach as variations of their respective base assumption. The categories identified are classification-based, nearest neighbor-based, clustering-based, statistical, information-theoretic, and subspace-based. In addition to pointing out the advantages and disadvantages of each approach, the authors analyze their computational complexity. They also observed that clustering-based techniques usually assume that the anomalous points do not belong to any cluster, e.g., DBSCAN and ROCK (Guha et al. 2000), or that the anomalous points are far away from the centroid of their nearest cluster, e.g., k-means and EM clustering. In both cases, anomaly detection is considered a by-product of clustering. Unlike our study, the authors did not perform any experimental evaluation or comparison of clustering-based anomaly detection algorithms.

Orair et al. (2010) presented the first comprehensive study exploring distance-based anomaly detection algorithms and their different efficient or approximate variations, which usually rely on pruning, sampling, or ranking strategies. The authors identified four common optimization strategies from the algorithms evaluated: two optimizations rely on clustering-based pruning and the other two are based on ranking strategies. They conducted a full factorial design experiment on the four types of optimizations identified and concluded that none of them is superior to the others on all data types. It is worth noting that this related work identifies common algorithmic techniques restricted to distance-based models (Knorr and Ng 1998; Ramaswamy et al. 2000; Angiulli et al. 2005), not clustering-based ones, which is the main focus of our work.

Zimek et al. (2012) studied the challenges and phenomena regarding anomaly detection algorithms in high dimensional Euclidean spaces, which are commonly referred to as the “curse of dimensionality”. The phenomena investigated are: the concentration of distances, which is the reduction of the usefulness of the measure for discriminating between near and far neighbors in high dimensionality; the discrimination of relevant or irrelevant attributes; the “hubness” effect related to the number of times a point is counted as one of the k neighbors of any other point, which is particularly relevant for algorithms based on distances to the \(k^{th}\) nearest neighbor; and the issues in efficiency. The authors further divided all the algorithms studied into two categories: algorithms interested in identifying subspaces to detect anomalies and those that do not, which are more concerned with efficient and effective solutions. The experiments performed explore the impact of the aforementioned effects on two anomaly detection algorithms only, i.e., k-NN outlier detection (Ramaswamy et al. 2000) and LOF (Breunig et al. 2000). They briefly analyze other anomaly detection algorithms, but without presenting a comprehensive, in-depth evaluation in these cases. Distinctly, our study presents a more extensive experimental evaluation, focused particularly on clustering-based anomaly detection.

Campos et al. (2016) extensively evaluated the effectiveness of 12 representative neighborhood-based anomaly detectors in the Euclidean space, such as k-NN outlier detection, kNN-weight (Angiulli and Pizzuti 2002), and LOF. Two collections of datasets were considered: those commonly used in the anomaly detection literature and those containing semantically meaningful anomalies. Several versions of these datasets were created and studied considering different pre-processing procedures. The authors also investigated the weaknesses and strengths of the most commonly used quality-evaluation measures and how to provide information on the relative performance of anomaly detection methods using a combination of several measures. They conclude that it is neither meaningful nor justified to claim that any of the methods studied has superior performance for the general case. This survey differs from our work in the restriction of evaluating only k-nearest-neighbor-based algorithms, and no clustering-based ones.

Goldstein and Uchida (2016a) studied the effect of using anomaly detection for data cleaning by removing the top anomalies from the training data to be given to a classifier for handwritten character recognition. The authors considered 9 anomaly detectors that are based on statistics, such as Gaussian mixture models (Lindsay 1995) and SVM (Amer et al. 2013), nearest neighbors, like k-NN outlier detection, LOF Breunig et al. (2000), and INFLO (Jin et al. 2006)), or clustering, e.g., CBLOF (He et al. 2003) and CMGOS (Goldstein 2014). INFLO was the only algorithm capable of improving the classification results. The results of the anomaly detection algorithms were not directly evaluated because the data used have no ground truth about the anomalies, and also because it was not the objective of this related work, which differentiates it from our work.

In a follow-up study, Goldstein and Uchida (2016b) evaluated 19 anomaly detectors on 10 datasets of different domains. The aspects considered were accuracy, stability of the outlierness scores generated, sensitivity to parameter configuration, runtime, and global/local anomaly detection behavior. They concluded that, in general, global anomaly detectors perform better than the local ones if the type of anomalies contained in the dataset is unknown. LOCI (Papadimitriou et al. 2003) was the least parameter-sensitive algorithm. Furthermore, algorithms based on clustering proved to be faster than those based on nearest neighbors. Unlike our work, this related work evaluated only the k-means variants of the clustering-based algorithms; note that we also evaluate density-based and ensemble-based algorithms, besides the k-means-based ones. Our work is also grounded in a more extensive collection of datasets.

Zimek and Filzmoser (2018) studied the origins and the development of statistical anomaly detectors and methods developed in a databases and data mining context from a shared viewpoint of data mining and statistics. The authors concluded that data mining methods usually focus on efficiency and applicability to large datasets and various types of data, e.g., deviation-based, density-based, or clustering-based outlier detection. By contrast, statistical methods are usually based on models, e.g., statistical tests, non-parametric statistical methods, or parametric methods assuming specific families of distributions. The former are more flexible in their applicability; however, they lost their original statistical notion and the probabilistic interpretability of the results. The latter have a clear evaluation by statistical tests but require the assumed model to fit the data, which restricts their applicability. In contrast to our survey, it is worth mentioning that only a few clustering-based anomaly detectors are discussed in this related work, namely, GLOSH (Campello et al. 2015), DBSCAN, k-means, and EM clustering. The focus of this related work is mainly general and theoretical, and no experimental evaluation is provided.

Zimek and Schubert (2018) briefly discussed seminal distance-based anomaly detection approaches, i.e., DB-outlier (Knorr and Ng 1998) and k-NN outlier, and those based on density or local approaches, e.g., LOF. The authors suggest that distance-based methods are considered as a subset of density-based methods because they primarily use distance as a simple density estimator that allows indexing techniques to speed up the computation of anomaly scores. They also highlight that improving the interpretability of the scores and explaining how anomalous each point is has been gaining attention lately. Unlike our work, this related work is purely theoretical with no experimental evaluation, and it does not address any clustering-based method.

Domingues et al. (2018) provide an experimental comparison of a selection of outlier detection methods, including LOF (Breunig et al. 2000), ABOD (Kriegel et al. 2008), iForest (Liu et al. 2008), and SOD (Kriegel et al. 2009a), but also probabilistic methods and methods from the (semi-)supervised learning area. However, no clustering-based method has been included.

ADBench (Han et al. 2022) is a recent research project that assesses 30 anomaly detection techniques, divided into 14 unsupervised, 7 semi-supervised, and 9 supervised methods. The evaluation considers three factors: the availability of ground truth labels (supervision), the types of anomalies, and the ability to handle noise and data corruption. The authors examined various degrees of supervision focused primarily on justifying the significance of supervised learning. Interestingly, they discovered that several simple unsupervised approaches outperformed many deep-learning-based supervised methods in their experiments. This study highlights the need for greater attention to algorithm selection, parameter optimization, the value of supervision, and prior knowledge regarding the specific type of anomaly being targeted. In contrast to our study, this related work does not assess anomaly detection methods based on clustering and utilizes datasets suitable for supervised learning only.

Also Marques et al. (2023) compare unsupervised and (semi-)supervised methods (one-class classification algorithms) for outlier detection. They discuss how to properly set up unsupervised methods in such a scenario for a fair comparison and compare the performance of a range of methods on datasets with various characteristics. Their second focus point is model selection methods. Among the compared algorithms are also two clustering-based methods, namely Gaussian mixture models (Bishop 2007; Dempster et al. 1977) and GLOSH (Campello et al. 2015), but a fundamental and essential difference from our study is the studied scenario of (semi-) supervised learning.

In conclusion, the above literature review shows that there is a lack of studies performing a thorough theoretical and experimental analysis of unsupervised, clustering-based outlier detectors. Our work addresses this gap in the literature. We would like to highlight the findings that some classic methods, in particular LOF and k-NN outlier, have been found to outperform deep-learning-based methods (Han et al. 2022); and, that clustering-based methods have received almost no attention in other comparative studies, while we will find that such clustering-based methods – especially the k-means-based methods, like KMeans−− (Chawla and Gionis 2013) – are on par with LOF and k-NN outlier. Hence, we argue that these methods should be included as baselines in future benchmarks of deep-learning methods. It is also worth noting that the existing literature suggests that clustering-based outlier detectors strengthen the relationship between the concepts of cluster and outlier, where the latter is seen as more than a simple by-product of the clustering task or more than the noise that needs to be removed to obtain a reliable clustering result.

3 Methods

The notion of outliers is strongly related to that of clusters (Hodge and Austin 2004; Chandola et al. 2009; Orair et al. 2010; Zimek and Filzmoser 2018). Clustering-based techniques explore the relationship between points and clusters to detect outliers by defining them as observations that do not fit the general clustering pattern. According to this approach, the outlierness of a point is defined considering at least one of the following questions:

  • Does the point not belong to any cluster?

  • Is there a large distance between the point and its nearest cluster?

  • Is the point part of a remote or small cluster (sometimes called ‘micro-cluster’)?

We categorize the clustering-based detectors according to their underlying clustering strategy and select representative methods of each category for evaluation. Table 1 lists the methods compared in our evaluation. Note that this table also presents the corresponding class implementing the named method in the ELKI 0.8.0 data mining framework (Schubert 2022), which is the one we use in our experimental evaluation.

Table 1 Methods evaluated and their implementation in the ELKI framework (https://elki-project.github.io/)
Full size table

3.1 k-means-based approaches

We begin by describing the methods based on the acclaimed k-means clustering algorithm (MacQueen 1967). The algorithm k-means performs clustering by minimizing the squared distances between each point and its closest cluster center, where the clusters are non-overlapping subsets/partitions of the dataset. It considers a fixed number of clusters k defined by the user.

In the following, we discuss anomaly detection methods that capitalize either on k-means or on one of its many variants.

3.1.1 KMeansOD

The algorithm k-means is occasionally used for outlier detection, e.g., as described by Han et al. 2012, where one leverages the distance from each point to its nearest center. The larger the distance, the more likely the point is an outlier. The method KMeansOD shown in Table 1 implements this idea through a scoring function that uses the aforementioned distance as the outlierness of a point.

Note that, for our study, we implemented two additional novel scoring functions that also determine the outlierness of a point based on the k-means clustering result. In the first variation, we attribute a score to every point that forms a unitary cluster or “singleton” using the distance from that point to the second closest cluster center. We do not use the distance to the closest center because the point is its own center. In the second alternative, the score of a point is the difference it induces in the k-means loss, which depends on the distance to the center and on the cluster size. Hence, outliers in small clusters score slightly higher than those in large clusters, because the center of a small cluster is influenced more by each observation than the center of a large cluster. This score is derived from the method of Hartigan and Wong (1979). Note, however, that these two new scoring functions did not yield noticeable differences in the experimental evaluation – which is not surprising, because they are closely related to the base strategy – and, thus, we do not further discuss them in the experimental analysis.

3.1.2 KMeans−−

The algorithm KMeans−− was introduced by Chawla and Gionis (2013) as an extension of the original k-means that also allows discovering a set L of outliers besides the k clusters on a dataset X. The set of outliers depends on the centroids identified because each point in L must be considerably distant from its closest centroid. This algorithm uses the same initialization and optimization criteria as k-means, with the difference that the centroids are computed on the set of points \(X \setminus L\), which also makes KMeans−− a variant of the trimmed k-means (Cuesta-Albertos et al. 1997). Consequently, the centroids also depend on the set L of outliers. After convergence, the outlierness score of every point in L is 1; the points in \(X \setminus L\) receive score 0. The size of the set L is a parameter to this method, and we use a relative size \(\vert L\vert =l\cdot \vert X\vert\) to accommodate for different data set sizes.

For our work, we evaluate the original approach with binary labeling; see the method KMeans−− in Table 1. We also consider a novel variation that calculates the outlierness scores according to the distance between each point and the center of its nearest cluster, as done for KMeansOD. We use the name KMeans−−* to refer to this new approach as shown in the table.

3.1.3 EMOutlier

Expectation Maximization (EM, Dempster et al., 1977) is an iterative algorithm that performs Gaussian Mixture Modeling by maximizing the probability of finding the parameters of multiple Gaussian distributions assumed to exist in a dataset. The algorithm alternates between two steps; in the Expectation step, it finds a lower bound function on the original likelihood using the current estimate of the parameters. In the Maximization step, it finds new parameter estimates by maximizing the lower bound function. Since the lower bound function is maximized at each iteration, the parameter estimates produced have a higher probability than those of the previous iteration, and ultimately converge to a maximum. Each distribution learned is often understood as a cluster of points with EM being seen as a clustering algorithm.

The algorithm EM has also been used in the literature for anomaly detection. Yamanishi et al. (2000) exploited EM by proposing an online mixture learning detector of outliers capable of handling both categorical and numerical data. Eskin (2000) introduced a variation of the EM algorithm in which a mixture model component is treated as an “anomaly” component that is drawn from a uniform distribution and assigned a low a priori probability. This approach seeks to identify the anomalous points as those that fit this particular mixture component. Han et al. (2012) also briefly mention the use of EM for anomaly detection. EMOutlier is part of the ELKI framework (Schubert 2022). It computes the outlierness of a point using this point’s contribution to the overall log-likelihood of the model, thus assigning high outlierness to points that do not fit any of the Gaussian clusters. By contrast, points that can be well explained using the clusters receive low scores, thus being considered normal. Other alternatives propose identifying a “noise” component while clustering noise-free points. For example, Banfield and Raftery (1993) model the noise component with a Poisson process and concentrate on robust estimation of cluster parameters. Coretto and Hennig (2011) also discuss the use of robust estimators for model-based clustering of data with Gaussian and uniform distributions.

For our work, we use the algorithm EMOutlier of the ELKI framework as the representant of the EM-based family of methods. See Table 1 for details.

3.1.4 SilhouetteOD

Silhouette width (Rousseeuw 1987), or just Silhouette, is an internal measure of clustering quality determining the consistency of a cluster based on distances from its points to other points of the same cluster and also to points of other clusters. This measure quantifies how similar a point is to its cluster compared to the other clusters. The Silhouette value ranges from − 1 to 1, where a value close to 1 indicates a point well associated with its cluster and poorly associated with neighboring clusters. Rousseeuw explores deeper heuristics of this measure by focusing on the graphical visualization of the individual Silhouettes (per point), but also presents the Average Silhouette Width (ASW) for the overall evaluation of the clusters, i.e., the average of all the Silhouette values computed for the entire dataset. The ASW is commonly used as a simple and intuitive clustering quality measure that does not rely on statistical model assumptions (Van der Laan et al. 2003; Arbelaitz et al. 2013; Batool and Hennig 2021). Since the clusters should be homogeneous and well separated, the larger the ASW, the better the clustering quality. An optimal clustering (i.e., with optimal k, if several values of k are compared) has ASW 1. An ASW of 0 is a poor result as it means that, on average, each point is no closer to the other points of its cluster than to the points in the nearest other cluster.

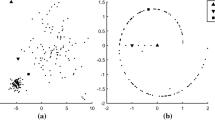
For anomaly detection, we use the Silhouette values of each point to determine how anomalous it is. The method SilhouetteOD (see Table 1) implements this idea. However, it turns out that this often does not work well: a global outlier may have a clear nearest cluster, with the second nearest farther away, and hence may still have a high Silhouette. Only points between two clusters have a low Silhouette, but if the clustering does not fit the data very well, these may not be outliers. We illustrate this problem in Fig. 1, where the smallest Silhouette values are not the low-density outliers even in this simple model but rather points halfway between the estimated cluster centers. For the method SilhouetteOD* shown in Table 1, we replace k-means with a k-medoids variation that directly optimizes the medoid-based variant of the Silhouette by Lenssen and Schubert (2022), and hence usually scores higher on ASW, trying to get more contrast into the Silhouette scores.

Fig. 1
figure 1

Illustration of Silhouette scores (red) on a mixture of two univariate Gaussians, for k-means clustering with \(k=2\). The estimated cluster centers are given by the cross marks; the Silhouette is 0 exactly halfway of the two cluster centers, while points in the low density regions of the generating distribution still have a Silhouette \(>0.5\) in this interval

Full size image

3.2 Density-based approaches

Here we describe approaches using density-based clustering. They all leverage the seminal clustering algorithm DBSCAN (Ester et al. 1996) or one of its many variants (Campello et al. 2020). DBSCAN is a density-based clustering algorithm broadly used in data mining and machine learning. It identifies clusters by examining dense regions of points separated by sparser regions. The algorithm begins by selecting a random point and examining its neighborhood within a given radius \(\varepsilon\); if the number of points within this neighborhood exceeds a predefined threshold \(minpts\), the point is labeled as a core point, and its neighborhood is expanded. By iteratively expanding the neighborhood of dense points, DBSCAN identifies other core points and connects them to form density-connected clusters. Points that are not core points, but are neighbors of them are considered border points, and those points that are neither core nor border points are deemed to be noise.

Moulavi et al. (2014) introduced an internal measure named Density-based Clustering Validation (DBCV) to assess the quality of density-based clusters. DBCV focuses precisely on density-based clustering algorithms because it considers the noise points – intrinsic to the density-based approach – and captures the shape and density properties of the clusters. It defines the “validity index of a cluster” based on the density connection between pairs of objects. More compact and separated clusters receive a positive validity index; if the internal density of a cluster is less than the density separating it from other clusters, the index is negative. The final result of DBCV is a weighted sum of the validity indices of all clusters; it produces a score ranging from − 1 to 1, where the higher the value, the better the clustering solution.

In the following, we discuss anomaly detection methods that capitalize either on DBSCAN or on one of its numerous variants.

3.2.1 DBSCANOD

The most straightforward manner to leverage DBSCAN for anomaly detection is to consider noise points as outliers. It has been described in the literature, for example, by Han et al. (2012). For our study, we go a little further by differentiating the outlierness of the points according to the point categories DBSCAN provides. The score is attributed to a point considering the category it belongs to: noise points receive score 1, border points receive 0.5, and core points receive 0. The method DBSCANOD (see Table 1) implements this approach.

3.2.2 OPTICS-OF

Algorithm OPTICS-OF (Breunig et al. 1999) employs the concept of local outlier detection by determining the outlierness of a point based on its closest neighbors. The algorithm computes an outlier factor to capture the relative degree of isolation (or outlierness) of each point, which is based on the concepts of core-distance and reachability-distance introduced before in the well-known clustering algorithm OPTICS (Ankerst et al. 1999). In its turn, OPTICS is a sequel of DBSCAN, and a precursor to the seminal Local Outlier Factor (LOF) Breunig et al. (2000). Distinctly from DBSCAN, it detects clusters of varying densities, which is achieved without introducing any parameter other than those of DBSCAN.

3.2.3 GLOSH

GLOSH (Campello et al. 2015) is an anomaly detector that capitalizes on hierarchical density estimates obtained from a clustering algorithm proposed by the same authors, HDBSCAN* (Campello et al. 2015). The hierarchy is based on the mutual reachability distance between a pair of points, which is defined as the maximum value among the distance between the two points and each point’s distance to its \(minpts\)-nearest neighbor. This approach allows the detection of outlying points in sparse regions. A mutual reachability graph represents the dataset with the points as vertices and their connections as edges. The weights of the edges are given by the mutual reachability distance between the corresponding pair of points. A minimum spanning tree is then built for the graph. Later, the edges of the tree are sorted by their weight, which allows extracting the hierarchical clustering structure in the form of a dendrogram.

After obtaining the hierarchy for the entire dataset, the outlier scores are calculated for each point considering the density difference around the point and the largest density of points within the nearest cluster. It is expected that points with scores close to 0 are in dense regions, while scores close to 1 are attributed to points (outliers) in sparse regions.

3.3 Ensemble-based approaches

OutRank (Müller et al. 2008) provides outlierness scores for the points of a dataset using the result of any subspace clustering algorithm. Positive scores are assigned to each point; the lower the score, the larger the outlierness of the point. Importantly, we consider OutRank ensemble-based because it detects outliers not by leveraging a specific method as it occurs for the approaches described previously, such as GLOSH, but rather by using a combination of several clustering results possibly obtained from any clustering method or even a combination of methods, especially considering subspace clustering methods.

The algorithm OutRank S1 of the ELKI framework implements the first scoring function proposed by Müller et al. (2008). It assumes that anomalies belong to tiny clusters or clusters formed in abnormally low-dimensional subspaces. Distinctly, the points considered “normal” belong to clusters with many points or clusters existing in subspaces of high dimensionality.

For our work, we consider two variants of OutRank using distinct clustering algorithms. The variant OutRank S1/D (see Table 1) leverages the algorithm DiSH (Achtert et al. 2007a), which detects clusters in subspaces of significantly different dimensionality by describing complex hierarchies of nested subspace clusters containing single and multiple inclusions. Distinctly, the variant OutRank S1/H (see Table 1) uses the algorithm HDBSCAN* described previously. For HDBSCAN*, we generate 100 random subspaces of a \(\delta\)-dimensional dataset to be analyzed, where each subspace is composed of \(\delta '\) dimensions with \(\delta '\) varying between 1 and \(\delta\). HDBSCAN* reports a flat clustering for each generated subspace, and then OutRank S1 provides the outlierness scores. The scores reported in the experimental evaluation are the average of the 100 scores calculated per point.

3.4 Non clustering-based approaches

The anomaly detectors most commonly used in the literature are not clustering-based. To put the results of clustering-based methods into perspective, we compare them also to state-of-the-art baselines representing the non clustering-based approaches, namely the algorithms KNNOutlier (Ramaswamy et al. 2000), LOF (Breunig et al. 2000), and iForest (Liu et al. 2008).

KNNOutlier is based on the principle that outliers are typically far from their nearest neighbors. The algorithm identifies outliers by calculating the distance between each point and its \(k^{th}\) nearest neighbor. Statistically, this can be seen as a simple density estimation. Points with significantly large distances (i.e., low density) are considered outliers. KNNOutlier is one of the simplest methods and can be considered a classic outlier model. It has been shown repeatedly to be competitive or even superior to various newer, more refined methods (Campos et al. 2016; Goldstein and Uchida 2016b). However, it may struggle with skewed data distributions and varying densities.

LOF measures the local density deviation of a point in its local neighborhood. It compares a point’s density to its neighboring points’ densities and assigns an outlier score accordingly. LOF can effectively detect outliers in data with varying densities and is robust to noise. However, it may be sensitive to the choice of parameters and has a high computational complexity. Like KNNOutlier, the classic method LOF has also been found competitive against more recent variations (Campos et al. 2016; Goldstein and Uchida 2016b).

iForest is an anomaly detection algorithm that operates on the principle of isolation. It builds a random forest consisting of isolation trees, where each tree isolates individual points through random feature selection and value splitting. Because each tree in the forest uses only a small subsample of the data, the method can easily be scaled to large data sets, and because the splits use only one attribute at a time, it also scales well with the data dimensionality. The algorithm computes the anomaly score of each point by averaging the path lengths across all trees. This can again be related to an approximate density estimation. Domingues et al. (2018) and Han et al. (2022) identified iForest as a competitive general purpose method in their comparative evaluation studies.

4 Research questions and experimental setup

In this section, we describe the experimental setup designed to answer the following questions, which are corresponding to the contributions presented in the introductory section.

  • Q1 Are clustering-based anomaly detection methods competitive in accuracy with those of the non-clustering-based state-of-the-art? (Sect. 5.1)

  • Q2 How resilient to data variation are the evaluated methods? (Sect. 5.2)

  • Q3 How resilient are they to parameter configuration? (Sect. 5.3)

  • Q4 Does effective clustering imply effective anomaly detection? (Sect. 5.4)

  • Q5 How do the methods scale in runtime? (Sect. 5.5)

We evaluate the 11 clustering-based anomaly detection methods and the 3 non-clustering-based methods described in Sect. 3. All methods are coded in Java under the ELKI 0.8.0 framework. The experiments were executed in three virtual machines each with the Fedora 30 x86_64 (Server Edition) operating system, 36 GB of RAM, a 50 GB hard disk, and an Intel Xeon E5-2640 processor with 2.6 GHz speed and 20 MB cache memory.

Table 2 Summary of datasets
Full size table

4.1 Datasets

We study the 46 real and synthetic datasets described in Table 2. The real ones were obtained from Campos et al. (2016). These are organized into two groups: (a) Used in the Literature, which consists of 11 datasets that appeared frequently in the research literature for evaluating anomaly detection algorithms, and; (b) Semantically Meaningful, which consists of 12 datasets initially intended for the evaluation of classification methods, where one or more classes have a natural semantic interpretation as anomalies. All datasets are publicly availableFootnote 1 and are already de-duplicated and normalized.

Importantly, the datasets of the semantically meaningful group often contain a large share of objects labeled as anomalies. Hence, Campos et al. (2016) offer downsampled versions of each dataset containing different percentages of outliers selected at random from the original datasets of classification. In our work, we consider the versions with \(5\%\) of outliers. Specifically, we use all the 10 versions available for each dataset having \(5\%\) of outliers, each of which was created from independent random downsampling executions. We process each version of each dataset independently and consider only the average result (single value per dataset) in our analyses, which is equivalent to the expected performance when \(5\%\) of outliers are selected at random from the original dataset of classification. Consequently, we study even more than the 46 datasets shown in Table 2 because each of the 12 datasets of the semantically meaningful group is, in fact, represented by 10 distinct versions with random variation from the original data. Due to this fact, we highlight each of these datasets in the table by adding an asterisk (*) after its name.

The synthetic datasets were generated to evaluate the algorithms in data containing clusters. We define each dataset based on the following seven configurations: the number of clusters; the cardinality; the number of dimensions; the positions of the clusters; the data distribution used to generate the points of those clusters; the percentage of outliers, and; the type of the outliers. There is one standard dataset (marked with \(\circledcirc\) in Table 2) and 16 variations for it. The standard dataset has 5 clusters, 10 thousand points, 2 dimensions, uniformly positioned clusters following Gaussian distributions, and \(5\%\) of outliers of the type global. In our notation, the dataset name encodes these configurations. The standard dataset is, therefore, named as 5c-10k-2d-u-gs-5p-g.

The variations were obtained by altering one configuration at a time and fixing the others. For example, datasets 2c-10k-2d-u-gs-5p-g and 10c-10k-2d-u-gs-5p-g were generated by varying the number of clusters from 5 to 2 and 10, respectively. The values considered per configuration are 2 (2c), 5 (5c), and 10 (10c) for the number of clusters; 1, 000 (1k), 10, 000 (10k), and 50, 000 (50k) for the cardinality; 2 (2d), 5 (5d), 10 (10d), 12 (12d), 15 (15d), and 20 (20d) for the number of dimensions; grid (gr), sine (s), and uniform (u) for the cluster positioning; uniform (u) and Gaussian (gs) distributions for clusters’ points generation; \(1\%\) (1p), \(5\%\) (5p), and \(10\%\) (10p) for the percentage of outliers; and global (g), local (l), and microcluster (mc) for the type of the outliers.

The 5- and 10-dimensional datasets with Gaussian clusters were generated by increasing the standard deviations of the Gaussian distributions of the standard dataset according to the square root of the number of dimensions. Therefore, the higher the dimensionality, the sparser the clusters. The datasets with 12, 15, and 20 dimensions maintain the standard deviation previously defined for 10 dimensions, and we add 2, 5, and 10 additional noise dimensions with random values, respectively, making anomaly detection more challenging.

Global outliers are noise points generated by a uniform distribution and away from any cluster. Local outliers are points obtained by the Gaussian distribution that generated one cluster, but are more than two standard deviations away from the mean. Microclusters (a.k.a. collective outliers) are subsets of points that deviate significantly from the rest; for this case, we determined the center of each microcluster by using a uniform distribution and verifying that it is far from any other cluster. Then, we generated a few nearby points for the microcluster using the same strategy of the regular cluster generation.

We also generated six datasets for the evaluation of scalability. Each dataset has a certain number of Gaussian clusters (i.e., 2, 5, and 10 clusters) and global outliers. The outliers represent \(5\%\) of the cardinality of each dataset, which is 125 thousand. For each number of clusters, two dataset versions with different dimensionality were generated, specifically, with 2 and 10 dimensions.

4.2 Evaluation measures

The studied methods return a complete ranking of the points based on their degrees of outlierness. We evaluate the ranking provided by each method for each dataset using the measures explained in the following, which depend on external ground truth that must exist for the data.

AUROC is the most popular evaluation measure in the literature. It regards the Area Under the Receiver Operating Characteristic curve (Goldstein and Uchida 2016a; Zimek et al. 2012; Campos et al. 2016; Zimek and Filzmoser 2018; Han et al. 2022), which is a curve obtained by plotting for all possible choices of n outliers the rate of true positives versus the rate of false positives. Other measures widely used in the literature (Campos et al. 2016) are the Average Precision, R-Precision, and Max-F1. Average Precision is the average of the precision values computed for each true outlier considering only the points up to its position in the ranking. R-Precision is the ratio of the recovered true outliers within the top n results, with n being the number of true outliers in the dataset, and hence offers only a low numerical discrimination. Max-F1 regards the F1 score (harmonic mean of precision and recall) at the optimum score threshold. The last three measures are commonly helpful to discriminate methods with similar results in terms of AUROC (Su et al. 2015; Davis and Goadrich 2006). Hence, we mainly use AUROC scores to judge the effectiveness of anomaly detection methods and leverage Average Precision, R-Precision and Max-F1 to obtain more information from each particular scenario.

It is worth mentioning that part of the results shown in our survey requires aggregating the evaluation values obtained from different datasets. Hence, we use the “adjusted by chance” (Hubert and Arabie 1985; Campos et al. 2016) versions of the measures Average Precision, R-Precision and Max-F1 because the expected values of the original, non-adjusted measures depend on the percentage of outliers in the dataset. Note, however, that we do not include “adjusted by chance” in the names of these measurements when presenting our findings for the sake of brevity and simplicity. Additionally, note that we do not adjust the AUROC values because a random ranking (result by “chance”) is expected to always produce a value 0.5 regardless of the dataset.

4.3 Parameter configuration

The parameters of each method were chosen within a reasonable range of values based on heuristics proposed by its original authors whenever they were available. Table 3 reports the values employed.

Table 3 Summary of parameter values
Full size table

For DBSCANOD, the values of the parameter \(\varepsilon\) range from \(1\%\) to \(20\%\) of the diameter (\(\gamma\)) of the dataset. Considering that all datasets are normalized to a unit hypercube, the diameter is estimated as a function of the data dimensionality (\(\delta\)) as \(\gamma = \sqrt{\delta }\). For the parameter \(minpts\), we considered nine percentages of the value suggested by the original authors (Ester et al. 1996). The same set of values is used for the parameters \(minpts\) of the algorithms OPTICS-OF and GLOSH; for the latter, the parameter \(minclsize\) (minimum cluster size) is always configured to be equal to \(minpts\) as suggested by the original authors (Campello et al. 2015).

The algorithms EMOutlier, KMeansOD, KMeans−−, KMeans−−*, SilhouetteOD, and SilhouetteOD* have each a parameter k to define the number of clusters. They were, therefore, equally configured using values from 1 to 50. The KNNOutlier and LOF have each a parameter k with distinct meanings, though. They refer respectively to the number of neighbors considered when identifying global and local neighborhoods, and were therefore configured differently. The parameter l of KMeans−− and KMeans−−* determines the number of outliers, and we use values relative to the dataset size. The parameter \(maxiter\) of EMOutlier, KMeansOD, KMeans−−, and KMeans−−* determines the alternative stopping condition for their convergent iterative approaches, which was set to a maximum number of 100 iterations. iForest always uses the parameter t with a fixed value, as suggested by the original authors (Liu et al. 2008), and \(\psi\) (sub-sample size) with sizes following powers of two up to \(30\%\) of n, where n is the dataset size.

The parameter \(\alpha\) is used as a weighting factor in the scoring functions of OutRank S1/D and OutRank S1/H. The value is fixed, as suggested by the original authors (Müller et al. 2008). In OutRank S1/D, the parameters \(\mu\) and \(\varepsilon\) are used by the plugged-in clustering algorithm DiSH. OutRank S1/H uses the parameter \(\lambda\) to determine the number of random subspaces; \(minclsize\) and \(minpts\) are employed by HDBSCAN* and configured following GLOSH.

It is worth noting that for each combination of parameters in nondeterministic methods, i.e., EMOutlier, KMeansOD, KMeans−−, KMeans−−*, SilhouetteOD, SilhouetteOD*, and iForest, we perform 10 independent executions and report the corresponding mean value for each evaluation measure.

5 Investigation

In this section, we present our experimental evaluation and report the results obtained. Each of the subsections in the following regards one of the research questions introduced before, in the beginning of Sect. 4, which correspond to the contributions presented in the introductory section.

5.1 Accuracy

This section intends to answer the question Q1: “Are clustering-based anomaly detection methods competitive in accuracy with those of the non-clustering-based state-of-the-art?”. To this end, we first performed the Friedman’s test to reject the null hypothesis that the methods provide statistically equivalent results (Demšar 2006). For the posthoc analysis (Benavoli et al. 2016), we abandoned the average rank comparison in favor of a pairwise statistical comparison: the Wilcoxon signed-rank test with Holm’s alpha correction (\(5\%\)). Finally, we employed a critical difference diagram (Demšar 2006) to depict the results of these statistical tests projected onto the average rank axis, with a thick horizontal line showing a clique of methods that are not significantly different in terms of AUROC, Average Precision, R-Precision, or Max-F1.

Fig. 2
figure 2

Critical difference diagrams showing the pairwise statistical difference comparison of the algorithms in their best configuration of parameters

Full size image

Figure 2 presents the critical difference diagrams regarding the best values per evaluation measure obtained by every method on each dataset considering all possible parameter configurations. We evaluate the results separately for each group of datasets, i.e., those used in the literature, the semantically meaningful ones, and the synthetic datasets. Regarding the datasets used in the literature, the algorithms KNNOutlier, KMeans−−*, OPTICS-OF, and GLOSH are generally at the top of the average rank considering the four measures. On the other hand, the algorithms SilhouetteOD and OutRank S1/H are the worst performers. We also note that the gap (amplitude) between the first and the last average rank in the diagrams is almost 8, which could be a significant difference in the performance. Nevertheless, the lines connecting all the methods shows that there is no statistically significant difference between the results they obtained. A similar scenario is seen in the semantically meaningful datasets, except for the appearance of the OutRank S1/D at the top of the ranking of R-Precision (Fig. 2g), separated from the second place by a small difference in the average rank. On the other hand, the results are considerably different regarding the synthetic datasets. We note that the amplitude in the average rank is almost 10 for these datasets, and there is a clear superiority of the method in the third place over the one in the fourth-place regarding the measures AUROC and Average-Precision. The KNNOutlier always gets the first place with the DBSCANOD and the EMOutlier following it in the successive positions. The KMeans−− and the OPTICS-OF show the worst performances. It is worth noting that both the DBSCANOD and the EMOutlier improved their performance compared to the other datasets. We believe it is because the synthetic data contain clusters following Gaussian distributions and a few outliers. Methods tend to perform better when their assumptions match the type of patterns present in the data.

Fig. 3
figure 3

Critical difference diagrams showing the pairwise statistical difference comparison of the algorithms w.r.t. the average values per evaluation measure obtained by every algorithm on each dataset considering all possible parameter configurations

Full size image

Outlier detection is mainly an unsupervised task. Hence, the results of the previous paragraph may not represent well-enough a real-world scenario. Rather, they represent an ideal scenario where we know a priori the correct parameterization to obtain the best possible result from each method and dataset. Figure 3 presents the critical difference plots regarding the average values per evaluation measure obtained by every method on each dataset considering all possible parameter configurations. We believe they assess a more plausible real-world scenario by simulating the use of values selected at random for each parameter from a reasonable range of values. In all three groups of datasets, the amplitude in the average rank is between 8 and 10, with the latter value observed in the synthetic data. For the first two groups, the algorithms LOF, KNNOutlier, KMeans−−*, and KMeansOD are generally the best performers. The good performance of the non-clustering-based methods KNNOutlier and LOF aligns with previous findings in literature, and shows that we chose a reasonable baseline. The OutRank S1/H, the SilhouetteOD, and the KMeans−− show the worst performances. For the synthetic datasets, the algorithms EMOutlier and KMeans−−* are always at the top of the ranking. From a statistical point of view, we deduce that none of the methods presents significantly better performance than the others considering the datasets used in the literature and the semantically meaningful ones. Distinctly, for the synthetic datasets, the algorithms EMOutlier and KMeans−−* perform considerably better than the other methods regarding the four measures.

Overall, we conclude that there is no significant superiority of the non-clustering-based algorithms over the clustering-based ones. Both approaches exhibit similar performance on the real data. On the other hand, a clear advantage of the clustering-based methods is seen on synthetic data, which we believe is determined partly by the setup of the datasets studied that involves the generation of clusters of normal data. Finally, it is worth noting that the continuous scores of the KMeans−−* lead to significant improvements compared to the binary labels of the original method KMeans−−, and it usually performs better than the standard variant KMeansOD, too.

5.2 Resilience to data variation

This section intends to answer the question Q2: “How resilient to data variation are the evaluated methods?”. We leverage boxplots to assess each method’s resilience considering various datasets. Each plot depicts the locality, skewness, and dispersion groups of a set of values obtained for one evaluation measure through their quartiles. The higher the dispersion in the set of values, the lower the resilience of the method. We first investigate the real datasets (Sect. 5.2.1) and then move on to the synthetic ones (Sect. 5.2.2).

5.2.1 Real data

Fig. 4
figure 4

Resilience of the methods regarding the best values obtained per evaluation measure in each dataset

Full size image

Figure 4 shows boxplots of the best values obtained by each method per evaluation measure and dataset. Every boxplot represents a set of values, each of which being the best result obtained by one method from one dataset regarding one measure. Here we discuss the results obtained from real data, that is, those depicted at the top two lines of plots shown in Fig. 4; the remaining results are discussed later in the paper. We observe that the AUROC values of the methods in all the real datasets generally present little dispersion, and they also present medians larger than 0.6. Thus, under the best parameter configuration, every method can detect outliers better than a randomized detector, although, for many applications, 0.6 will be much too low to be useful. On the other hand, the best values of Average Precision, R-Precision, and Max-F1 (all of them adjusted for chance) tend to be considerably lower, with medians often smaller than \(\approx 0.4\). We believe that there exist three reasons for these undesired results. Firstly, the datasets have a large variety of domains. Secondly, the number of outliers and inliers is not balanced, with outliers accounting for approximately \(5\%\) of the data, which is common in anomaly detection scenarios. Thirdly, the datasets were usually labeled for a classification task, not for outlier detection, and may contain anomalous objects that nevertheless belong to the majority class and are labeled as “normal”. Furthermore, the relatively large spread of values in these three measures shows that, except for SilhoutteOD, all methods have a low resilience concerning the type of data under analysis even when using their best possible parameter configurations. Overall, both the clustering-based and the non-clustering-based approaches present comparable resilience to the data variation assuming that the optimal setup for each method and dataset is known a priori.

Fig. 5
figure 5

Resilience of the methods regarding the average of the values obtained per evaluation measure in each dataset

Full size image

The boxplots corresponding to the average values obtained by each method per evaluation measure and dataset are shown in Fig. 5. We note that the AUROC scores for the datasets used in the literature have a moderate dispersion of nearly 0.5 between the minimum and the maximum values of the plots, and the medians range from 0.5 to 0.9. For the other evaluation measures, the algorithms KMeansOD, KMeans−−* and KNNOutlier have large spread values with low resilience to data variation. The SilhouetteOD and the SilhouetteOD* exhibit much better resilience, though. Unfortunately, it is not a positive result because their median values are very low. In the semantically meaningful datasets, the dispersion of AUROC values is approximately 0.4, thus being smaller than that of the other group of real datasets, and the medians range from 0.5 to 0.8. Additionally, the other evaluation measures exhibit reduced dispersion of values, such as for the algorithms KMeansOD, KMeans−−* and KNNOutlier, which indicates moderate resilience to data variation regarding all methods and this group of datasets. Overall, when considering the results in a randomized configuration scenario, the clustering-based methods are slightly superior to the non-clustering-based ones in terms of their resilience to variation in the data analyzed.

5.2.2 Synthetic data

In general terms, most methods have similar resilience to data variation when evaluated considering our real datasets. Nevertheless, we have little knowledge about the characteristics of these datasets, such as the underlying data distributions, the types of the outliers, if there are irrelevant dimensions, and a number of other unknown features that may impact the results of the methods. For this reason, we also evaluate the methods using synthetic data in a controlled experimental environment. We intend to glimpse if there are superior algorithms regarding the resilience to data variation under certain conditions.

Figure 4 shows that many methods are highly resilient to data variation when considering their best results obtained from the synthetic datasets; see the last line of boxplots at the bottom part of the figure. Most boxes in the plots depict very concentrated values and large medians of at least 0.8 or so for the four evaluation measures, which indicates high resilience and good performance. It is important to emphasize that even an algorithm using random scoring could also obtain a high resilience with very low dispersion of values. Nevertheless, its performance would be poor, such as having a median of around 0.5 regarding AUROC. For instance, the KMeans−− presents a lower-than-average performance, although it is one of the most resilient methods. On the other hand, the OPTICS-OF and the LOF present low resilience and medium-to-low performance. The OutRank S1/D remains exhibiting an average resilience with a median above 0.8 in all evaluation measures. Overall, under the best parameterization conditions, most methods of both the clustering-based and the non clustering-based approaches demonstrate higher resilience on the synthetic datasets than that seen in the real datasets.

Figure 5 presents considerably distinct results for the group of synthetic datasets compared with those of the other two groups. As described before, this figure depicts the resilience of the methods regarding the average values obtained per evaluation measure in each dataset. Note that the medians of AUROC values are well above 0.6 for the synthetic data and generally better than those of the real data. The medians of the other measures are also considerably better for the synthetic data compared with the real data. The algorithms EMOutlier, KMeansOD and KMeans−−* stand out as the most resilient ones also having nearly-perfect medians close to 1.0 for the four measures. The KMeans−− presents high resilience too, but its median values are all considerably lower. On the other hand, the remaining methods exhibit considerably worse resilience by being much more susceptible to variation in their effectiveness in the synthetic data than in the real data. Provided that the medians of these methods are considerably better for the synthetic data, there is also more room for variation in the scores obtained, with some particular configurations performing much better or worse than others. Overall, in a randomized parameterization scenario, the non clustering-based methods are less resilient to synthetic data variation than the clustering-based ones, especially when considering the algorithms EMOutlier, KMeansOD and KMeans−−*.

Fig. 6
figure 6

Resilience of the methods with respect to specific variations in the synthetic data. We consider the average of the values obtained per method and dataset in each measure

Full size image

Figure 6 presents results regarding the resilience of the methods to specific variations in our synthetic data. Each row of plots regards a subset of our synthetic datasets in which all characteristics are equal to those of our standard dataset except for one single characteristic. For example, the first row of plots regards datasets having distinct numbers of clusters while the remaining characteristics are the same as in the standard dataset. Once again, we consider the resilience of the methods regarding the average of the values obtained per evaluation measure in each dataset, because they assess a more plausible real-world scenario than the evaluation considering the best values obtained per dataset. Considering the datasets with different numbers of clusters, i.e., 2, 5, and 10 clusters, the AUROC medians are all above 0.6. The EMOutlier stands out not only for having a high resilience, but also for presenting a median of almost 1.0 (unsurprisingly, as it matches the data generation process very well). Similar results are seen for the algorithms KMeansOD and KMeans−−*. The DBSCANOD and the KMeans−− also show very similar results in terms of high resilience, but their median values are less than \(\approx 0.7\). The remaining methods demonstrate moderate resilience with dispersion around 0.2. In the other three evaluation measures, we see that the KMeans−−, the SilhouetteOD, and the DBSCANOD are highly resilient to data variation, but they present low effectiveness with medians below 0.4. The EMOutlier is highly resilient too; distinctly, this method is highly effective presenting medians above 0.9. The other methods demonstrated moderate or low resilience with the KNNOutlier being the one with the lowest resilience. Overall, when considering the variation in the number of clusters, it is evident that most clustering-based methods are more resilient and perform better than the non-clustering-based methods.

We now move on to the datasets with varying cardinalities, i.e., 1k, 5k, and 10k. In the four evaluation measures, the most resilient methods are the EMOutlier, the KMeansOD, the KMeans−−*, the KMeans−−, and the SilhouetteOD. Note, however, that the last two methods have low effectiveness with medians much smaller than those of the other methods. Regarding AUROC, the methods OPTICS-OF, SilhouetteOD*, KNNOutlier, and LOF presented the lowest resilience with dispersion of values close to 0.5. The methods DBSCANOD, OPTICS-OF, KNNOutlier, and LOF are the least resilient ones regarding the remaining three measures, with dispersion of values close to 0.9. Overall, considering the variation in the data cardinality, we evidenced a higher impact on the effectiveness of the non-clustering-based methods compared to the clustering-based ones. The latter are again more resilient to data variation, especially considering the methods EMOutlier, KMeansOD, and KMeans−−*.

Regarding the datasets with different numbers of relevant attributes, i.e., 2, 5, and 10 relevant attributes, all methods had medians of AUROC values above 0.6. The methods EMOutlier, KMeansOD, KMeans−− and KMeans−−* are the most resilient ones in all evaluation measures, but the KMeans−− is considerably less effective than the others. The DBSCANOD stands out as the least resilient method considering all evaluation measures, with values of dispersion being often around 0.6. Overall, when varying the number of relevant attributes, both clustering- and non clustering-based approaches present a similar degree of resilience. For datasets with varying numbers of irrelevant attributes, i.e., 2, 5, and 10 irrelevant attributes, we see that the DBSCANOD continues to be the least resilient method regarding AUROC. Nevertheless, the remaining methods generally presented higher resilience compared to the previous data variation. For the other three measures, the DBSCANOD continued to be the least resilient method, followed by the SilhouetteOD* whose medians are around 0.4. The algorithms EMOutlier, KMeans−−, and OutRank S1/D are the most resilient ones, but only the first method also presents high effectiveness. Overall, the non clustering-based methods are more resilient than the clustering-based ones to variation in the number of irrelevant attributes.

For the datasets with varying cluster positioning, i.e., grid-, sine-, and uniform-based positioning, most methods presented high resilience with dispersion values often bellow 0.1 regarding the four evaluation measures. The exceptions are the methods DBSCANOD, OutRank S1/D, KNNOutlier, and LOF because they presented moderate resilience to the cluster positioning pattern. A similar result can be seen in the next data variation, where the clusters are generated by different distributions, i.e., Gaussian and uniform distributions. The main exception is that the SilhouetteOD* appeared as the least resilient method in this case, followed by the KNNOutlier, the OutRank S1/H and the LOF. On the other hand, the DBSCANOD greatly improved its resilience and obtained values of dispersion as low as 0.1, although its effectiveness was very much low. Overall, considering the variation of the clusters’ positioning and of the distribution of their instances, the clustering-based methods showed slightly better resilience than the non clustering-based ones.

For the last two scenarios, we consider datasets with distinct percentages of outliers, i.e., \(1\%\), \(5\%\), and \(10\%\) percent, as well as with different outlier types, including local, global, and collective outliers. In the first scenario, based on AUROC values, we see that the methods EMOutlier, KMeansOD, KMeans−−*, OutRank S1/D, SilhouetteOD, iForest, and KNNOutlier exhibit high resilience with dispersion as small as 0.1. Except for the SilhouetteOD, all of these methods were also effective with medians above 0.8. The remaining methods demonstrated lower resilience with dispersion between nearly 0.2 and 0.5, and moderate effectiveness. Considering the other three evaluation measures, the EMOutlier, the KMeansOD, and the KMeans−−* stand out as the most resilient methods with dispersion close to 0.1. These methods were also the most effective ones with medians above 0.9. The least resilient methods are the LOF and the OPTICS-OF with dispersion as large as 0.8. Additionally, it is worth noting that the OutRank S1/D was much less resilient in these three measures than in the AUROC measure. A reason could be that the subspace clustering algorithm DiSH used by OutRank S1/D might be identifying tiny clusters of anomalous points, especially when the percentage of outliers is large. The larger the number of outliers the larger the probability they form clusters. Such potential clusters of outliers might have small cardinalities and exist only in subspaces, but they would still be detected by DiSH and considered as less anomalous by OutRank S1/D. It might put inliers ahead of very few outliers in the rankings of points, thus only marginally impacting the AUROC values because a small number of mistakes often have little impact in this metric; distinctly, their impact is more noticeable in the other three measures.

We now move on to the last scenario. Note that most methods struggle in both resilience and effectiveness when the type of the outliers varies. When considering the AUROC measure, the EMOutlier, the KMeans−− and the OutRank S1/D remain as the most resilient methods with dispersion around 0.1. Distinctly, the methods GLOSH, SilhouetteOD, SilhouetteOD*, and LOF stand out as the least resilient ones with dispersion as large as 0.6. For the other evaluation measures, the methods were in general even less resilient; the least resilient ones are the GLOSH, the SilhouetteOD*, and the LOF. Unfortunately, the most resilient methods were the ones that constantly presented low effectiveness, including the SilhouetteOD, and the OPTICS-OF. Ultimately, in these last two scenarios, no approach stood out in resilience; however, when considering the medians of the values in all evaluation measures, it is plausible to state that the clustering-based methods demonstrated better performance.

In conclusion, we highlight that both varying the percentage and the type of the outliers harmed the resilience of the methods generally. On the other hand, varying the number of instances, the clusters’ positions or the distribution of their instances had minor impact on the method’s resilience. Overall, when considering synthetic data, the clustering-based methods were once more slightly superior to the non-clustering-based ones in terms of their resilience to variation in the data analyzed.

5.3 Resilience to parameter configuration

Here we refer to question Q3: “How resilient to parameter configuration are the evaluated methods?”. We first consider one dataset at a time and later present an overall view of the results considering all the datasets studied.

5.3.1 Analysis per dataset

Figure 7 shows the dispersion of the evaluation measures when varying the parameter configuration of each method. That is, each boxplot illustrates the dispersion of the evaluation measures obtained for each method when using the many parameter configurations shown in Table 3. For this purpose, we consider three datasets (i.e., Lymphography, Glass and Wilt) selected to represent distinct levels of difficulty according to a score introduced by Campos et al. (2016). This score is defined as the average of the (binned) ranks of all outliers reported by a given set of outlier detectors for one dataset. If a dataset has a low score, it contains outliers that are relatively easy to detect using most methods. A high score means that all or most methods have high difficulty in detecting the outliers. The score values range from 1 to almost 10, representing a perfect and a random ranking respectively. Importantly, note that the scores of difficulty were generated by Campos et al. (2016) using a different set of methods than ours; however, we consider it plausible to use these scores in our work due to the large number and variety of approaches employed.

Lymphography is the easiest dataset; it has a low difficulty score of nearly 1. We confirm this fact by observing that the AUROC values obtained by most methods have medians above 0.7, although no method manages to obtain a median larger than 0.9. Under this evaluation measure, the most resilient methods are the EMOutlier, SilhouetteOD, and KNNOutlier. The least resilient ones are DBSCANOD, GLOSH, OPTICS-OF, and OutRank S1/H. Regarding the measure Average Precision, the OPTICS-OF is the most resilient method, but it always presented low quality results. Distinctly, the EMOutlier and KMeansOD presented much better effectiveness with slightly lower resilience to parameter configuration. The methods KMeans−−, KMeans−−*, and LOF are the least resilient ones. Similar results are seen for the other two measures.

Fig. 7
figure 7

Resilience to parameter configuration considering 3 datasets. They have high, medium and low levels of difficulty

Full size image

Glass has a difficulty score of about 4.5 and can, therefore, be considered a medium-difficulty dataset. Looking at the AUROC values reported, we can confirm that this dataset is more challenging than the Lymphography because four methods (and not only 2) obtained medians below 0.6. In this case, most methods (i.e., EMOutlier, GLOSH, KMeansOD, KMeans−−, KMeans−−*, iForest, KNNOutlier, and LOF) showed high resilience concerning parameter variation. Reviewing the results of the remaining three evaluation measures, we notice that not only the effectiveness of all methods is low, with Average Precision and R-Precision smaller than \(\approx 0.2\) and Max-F1 bellow \(\approx 0.4\), but also the dispersion of values was reduced, thus leading to a phenomenon that we shall call “forced high resilience”. The higher the difficulty score of a dataset, the higher the resilience of the methods that analyze it. This phenomenon may be explained by a direct relationship between the difficulty of a dataset and the resilience of a method that analyzes it. The more difficult it is to detect the outliers in a dataset, the more compact is the dispersion of values of an evaluation measure; and, the measurements are usually concentrated in values representing low performance.

Wilt is a very difficult dataset with a difficulty score of \(\approx 6.5\). According to the reported AUROC values, all methods had medians below 0.5, except for the EMOutlier and the OutRank S1/D whose medians are slightly larger than 0.6. Furthermore, we notice that the dispersion of values is small (\(\approx 0.1\)), once again demonstrating the phenomenon of forced high resilience. The few exceptions are the OPTICS-OF and the OutRank S1/D with dispersion of \(\approx 0.4\). In the other three evaluation measures, we again confirm the aforementioned phenomenon. Since this dataset has a high degree of difficulty, all methods have very high resilience and poor effectiveness.

The results obtained from the remaining datasets are reported in Figs. 12 and 13 of Appendix A. Note that the datasets with known difficulty scores as reported by Campos et al. (2016) are presented in ascending order of difficulty. The datasets with unknown scores are shown separately. Let us now summarize these results while also contrasting them with the degree of difficulty of each dataset. It is worth noting that 18 out of the 23 datasets studied by Campos et al. (2016) were characterized as being difficult; 6 of them come from the group of datasets commonly used in the literature, and the remaining 12 are from the semantically meaningful group. Starting with the group of datasets typically used in the literature, we confirm that the datasets ALOI and Waveform are difficult with all methods struggling to detect the outliers. Also, WPBC is the most challenging dataset of the group. All methods experienced forced high resilience with very low effectiveness regardless of parameter configuration. Distinctly, the datasets WBC and WDBC are much easier. It was confirmed because most methods achieved relatively low resilience and high values in all four evaluation measures. As a contribution of our survey, we can say that Ionosphere is a moderately easy dataset with most methods performing well, except for some very resilient methods that presented low effectiveness. For KDDCup99, PenDigits and Shuttle, all methods obtained resilience and effectiveness similar to those observed in Glass. Therefore, we characterize them as datasets of medium difficulty. Overall, clustering-based and non-clustering-based methods reported similar resilience to parameter configuration without considerable distinction between the approaches.

Finally, in the group of semantically meaningful datasets, the results we obtained also corroborate the levels of difficulty reported by Campos et al. (2016). The clustering-based methods presented low resilience and high effectiveness in the datasets with a low difficulty score (\(\lessapprox 4\)). We also observed forced high resilience in the datasets of medium-to-high difficulty (\(\gtrapprox 6\)). Importantly, the non-clustering-based methods demonstrated better performance than the clustering-based ones for the datasets with low-to-medium difficulty. That is, they obtained better quality of the results in terms of the evaluation measures and higher resilience to parameter configuration.

5.3.2 Overall view

Motivated by the previously presented results, we elaborated Fig. 8 as an “overall view” to depict how resilient the methods are when varying their parameter configuration. We consider the average and the standard deviation of the evaluation measurements. The horizontal axis of each quadrant represents the average of the values of one measurement obtained from a method when evaluating one dataset; the vertical axis presents their corresponding standard deviation. We divided the 18 datasets characterized by Campos et al. (2016) into three groups according to their score of difficulty: Lymphography, Parkinson, WBC, and WDBC are considered to have a low degree of difficulty; PageBlocks, Stamps, HearDisease, Hepatitis, Arrhythmia, InternetAds, Glass, and Cardiotocography have a medium difficulty, and; SpamBase, Pima, ALOI, Annthyroid, Wilt and Waveform have a high degree of difficulty. Each dataset is represented by a unique marker, while each method has a unique color. Consequently, a marker appears in 12 different positions, each time drawn with a different color according to the method being considered.

Under this setting, the markers are positioned in such a way that the lower the standard deviation in the vertical axis of each plot, the higher the dispersion of the average results shown in the horizontal axis. It is possible to note that this dispersion is reduced even further as the level of difficulty of the datasets increases. We also notice that the results get more concentrated in values that represent low performance as the degree of difficulty becomes higher. For example, the results regarding the datasets of medium and high difficulty are often close to 0.5 in the AUROC measure and near 0 in the Average Precision, R-Precision, and Max-F1 measures.

Fig. 8
figure 8

Overall view of the resilience to parameter configuration. We plot the average versus the standard deviation of the evaluation measurements obtained from each method when analyzing each dataset under distinct parameter configuration, distinguishing methods by color and datasets by shape of the plotted symbols. The results are grouped by the degree of difficulty of the datasets to better represent distinct scenarios

Full size image

In the low-difficulty datasets, we notice that the AUROC averages are mostly above 0.4, with some values getting close to 1.0. The methods EMOutlier, KMeansOD, KMeans−−*, KNNOutlier, and LOF stand out by reporting averages around 0.9 and standard deviations smaller than 0.1, thus presenting both high effectiveness and high resilience to parameter configuration. The methods SilhouetteOD and KMeans−− also present high resilience, but with lower quality of results. The least resilient methods are DBSCANOD, GLOSH, and OPTICS-OF, presenting standard deviations close to 0.2 despite having relatively good effectiveness with average AUROC values around 0.8. The SilhouetteOD* is the worst-performing method with standard deviations close to 0.2 and averages between 0.2 and 0.6. Once again, the Average Precision, R-Precision and Max-F1 measurements show similar patterns, except for the fact that the OPTICS-OF and the OutRank S1/D reported considerably large standard deviations between 0.3 and 0.4, i.e., low resilience. Overall, these datasets do not represent tough challenges; most methods demonstrated high performance both in terms of resilience and in the quality of the results, and a few others report low resilience and accuracy. Considering this, we conclude that there is no remarkable superiority between clustering and non-clustering-based methods regarding resilience to parameter configuration for these datasets.

Concerning the datasets of medium difficulty, GLOSH had the largest variations in the AUROC measurements. It presented large standard deviation values of around 0.2 and average values ranging from 0.2 to almost 0.9. Hence, low resilience and unstable effectiveness. The same did not occur for the other methods, whose AUROC results are usually concentrated in particular regions of the plots, thus indicating better stability. For example, the methods EMOutlier, KMeans−−*, KNNOutlier, and LOF reported averages close to 0.8 and high resilience with standard deviations smaller than \(\approx 0.1\). On the other hand, we have the methods DBSCANOD, KMeans−−, SilhouetteOD, and OutRank S1/H with high resilience, but averages close to 0.5 depicting near-random results. Concerning the Average Precision, R-Precision, and Max-F1 measures, we see that the methods GLOSH, OPTICS-OF, OutRank S1/D, and OutRank S1/H are the least resilient ones. Let us highlight the specific case of GLOSH when analyzing the dataset Arrhythmia. The average values are relatively high, being close to 0.6 for the Average Precision and near 0.8 for both R-Precision and Max-F1. However, the values of standard deviation are also high, which clearly indicates low resilience to parameter configuration. Analyzing the most extreme cases, the methods EMOutlier, KMeans−−*, KNNOutlier, and LOF appear as the best performers and most resilient, while the DBSCANOD, the KMeans−− and the SilhouetteOD reported much lower performance yet with high levels of resilience. As the difficulty of the datasets increases, the dispersion of the results shrinks, with the markers getting closer to coordinates representing low performance on each evaluation measure. Therefore, we observe once again the phenomenon of forced high resilience (Sect. 5.3.1).

For the datasets of high difficulty, the dispersion of the results contracts even further for all evaluation measures. That is, the standard deviations are lower than those seen before, and the averages are closer to values representing poor effectiveness. The only exception is the method OutRank S1/D when analyzing the dataset Waveform. We observe very high standard deviations in this particular case, thus characterizing OutRank S1/D as the most unstable method for this dataset. Compared to other methods, it occasionally presents better effectiveness when using particular configurations. Despite of this exceptional case, we cannot notice overall superiority of any method over the others because the results are mostly agglutinated. It exemplifies once again the phenomenon of forced high resilience discussed before.

In summary, the results reported in this section show that the more difficult the dataset, the more resilient to parameter configuration are the methods. Nevertheless, it is not a positive characteristic because the methods tend present low effectiveness regardless of the parameter configuration for difficult datasets. This implies that, in data of low-to-medium difficulty, there is little chance of achieving optimal performance using arbitrarily chosen parameter values, because the methods return both high- and low-quality results as their parameter configuration varies. Importantly, these results emphasize the need for appropriate parameter selection strategies. Obviously, the effectiveness tends to decrease as the difficulty of the data increases. Also, it is worth mentioning that our analysis considered the level of difficulty of a dataset, and not its dimensionality. Since each method generally reported similar performance for data of similar difficulty (which often have considerably distinct dimensionalities), the degree of difficulty may not be directly correlated with the data dimensionality, as it is often assumed in the literature. Finally, we could not notice remarkable superiority between clustering and non-clustering-based methods regarding their resilience to parameter configuration.

5.4 Automatized parameter selection

This section investigates the question Q4: “Does effective clustering imply effective anomaly detection?". For this purpose, we verify whether or not it is feasible to enhance the selection of parameter values of the clustering-based anomaly detectors by automatically filtering out those values that lead to poor clustering quality. As discussed in Sect. 1, previous works support the strong relationship between the concepts of cluster and outlier, considering the latter more than a simple by-product of the former or more than the noise that must be eliminated to obtain a reliable clustering result. For this purpose, we study the correlation between the four measures used so far (i.e., AUROC, Average Precision, R-Precision and Max-F1) and two well-known internal measures of clustering quality assessment: ASW and DBCV. As described in Sect. 3, both the ASW and the DBCV assess the quality of a set of clusters according to certain assumptions about what constitutes an appropriate clustering result. The ASW evaluates the compactness and the separability of the clusters; distinctly, the DBCV compares the density within the clusters and the density of the space regions separating the clusters.

The anomaly detection methods considered in this section are the SilhouetteOD and the DBSCANOD. Like any clustering-based outlier detector, both methods execute an initial clustering procedure and later use the clusters identified to compute outlierness scores. The SilhouetteOD uses the k-means clustering algorithm. The DBSCANOD employs the DBSCAN algorithm. Once again, we consider the same parameterization heuristics discussed before and presented in Table 3 of Sect. 4.3. We used the measures ASW and DBCV to assess the clustering results obtained by the methods k-means and DBSCAN, respectively, and the measures AUROC, Average Precision, R-Precision and Max-F1 to evaluate the results of anomaly detection. Aimed at discovering whether or not it is possible to obtain a good anomaly detection result based on a good prior clustering, we then performed the following: we calculated the Pearson correlation along with the confidence interval between all clustering quality and anomaly detection assessment values (e.g., ASW vs. AUROC or DBCV vs. AUROC) to measure the strength of the linear association between those two variables; later, we chose the configurations leading to the best clustering quality to verify if they also allow for appropriate anomaly detection.

Fig. 9
figure 9

Correlation between the measure of clustering effectiveness ASW and the measures of anomaly detection quality AUROC, Average Precision, R-Precision and Max-F1 (left: correlation coefficient with confidence interval, right: anomaly detection quality for different clustering results, where the best clustering result according to ASW is highlighted)

Full size image

Figure 9 reports results regarding the correlation between the effectiveness of the clustering method k-means and that of the outlier detector SilhouetteOD. On the left side of the illustration, we report the confidence interval width (i.e., the upper and lower bounds of the confidence interval – each shown as a black dash) and the corresponding correlation coefficient (i.e., the average of the values contained in the confidence interval – shown as a red dot) for each dataset. Remember that the confidence interval for a correlation coefficient is the range of values likely to contain the “true population correlation coefficient” at the \(95\%\) confidence level (Lane 2003). Especially for the datasets of low difficulty, such as the Lymphography dataset, we notice a clear positive correlation between the effectiveness of the clustering method and that of the anomaly detector under the same parameter configuration. Overall, the datasets used in the literature had more positive correlation coefficients than those of the semantically meaningful group. The plots on the right side of Fig. 9 show the effectiveness of the anomaly detector when using distinct parameter configurations. The configuration that maximizes the clustering quality for a dataset is highlighted with a red dash. In addition to confirming what was observed in the confidence interval plots, we note that the best-clustering-quality markers often regard appropriate outlier detection, especially when considering the datasets of low-to-medium difficulty. On the other hand, it is noticeable that the most challenging datasets, such as Wilt, often lead to no apparent positive correlation or even to negative correlations, which restricts the ability of automatically discarding any parameter value for these datasets.

Fig. 10
figure 10

Correlation between the measure of clustering effectiveness DBCV and the measures of anomaly detection quality AUROC, Average Precision, R-Precision and Max-F1 (left: correlation coefficient with confidence interval, right: anomaly detection quality for different clustering results, where the best clustering result according to DBCV is highlighted)

Full size image

Figure 10 regards the correlation between the effectiveness of the clustering method DBSCAN and that of the anomaly detector DBSCANOD. When evaluating the left side of the illustration, we notice that the widths of the confidence intervals are smaller than those obtained with the methods k-means and SilhouetteOD. This likely is because the number of samples used to calculate the confidence intervals is larger now. As shown in Table 3, there are nearly 430 different configurations for DBSCANOD and only 50 for SilhouetteOD. Consequently, the probable value of the true correlation coefficient is more limited, which makes it possible to infer the correlation type with more certainty. Overall, we cannot see remarkable differences between positive and negative correlations in the results reported. However, the trend of strong positive correlations in datasets with low difficulty (e.g., HeartDisease) remains. Note that we do not report results for the datasets Arrhythmia, Hepatitis and InternetAds. This is because DBSCAN always obtained DBCV\(=0\) for these datasets regardless of the configuration used, and it made both the correlation calculation and the parameter selection unfeasible.Footnote 2 When analyzing the right side of the illustration, we note that no parameter selection criterion could be applied for these three datasets; that is, no configuration determines the best clustering quality. This generates exception cases in which the marker points to all effectiveness values obtained by DBSCANOD. In the remaining datasets, we note that there is no convincing correspondence between the configurations with the best clustering quality and best effectiveness of the outlier detector.

In summary, the use of a mechanism to filter out parameter values leading to poor clustering quality may present limitations or exceptions in real-world applications. However, it offers the possibility of reducing or eliminating the randomness of applying a parameterization heuristic. This mechanism is supported by the abundant and well-known literature on internal evaluation measures and validation of clustering solutions, but it has been notably overlooked in the outlier detection domain; see the discussion in the previous Sect. 2. Consequently, future work on this topic is very much needed. This is especially true when we consider that there is no a priori information about which points are anomalous in a typical anomaly detection application, and, therefore, the results must be evaluated by domain experts, which increases both the time and the complexity of the parameter selection stage.

5.5 Scalability

This section answers the question Q5: “How do the methods scale up?”. One of the most important challenges in anomaly detection is the ability to tackle large datasets. Hence, we report scalability results for the 14 methods evaluated considering the 6 synthetic datasets created with this purpose and described in Sect. 4.1. We process subsets of each dataset containing \(12.5\%\), \(25\%\), \(50\%\) and \(100\%\) of the instances selected randomly. It is worth mentioning that we sampled proportional percentages of outliers and inliers to maintain the original characteristics of the data. Each method was tested considering the many parameter configurations shown in Table 3. For each configuration, we performed 10 independent executions and computed the average runtime. We then report the average of the average values obtained from all configurations. To make the execution of these experiments feasible, we also defined time and main memory consumption limits of 5 hours and 10 GB, respectively. All executions exceeding any of these limits were aborted and, therefore, the corresponding result is not reported.

Fig. 11
figure 11

Runtime vs. data size for 2- and 10-dimensional datasets with varying numbers of clusters and \(5\%\) of outliers. The results are shown in log-log scale for clarity of the illustration

Full size image

Figure 11a reports the runtime measurements regarding the 2-dimensional dataset with 2 clusters and outliers. The results are shown in log-log scale for clarity of the illustration. The two gray lines exemplify linear (Slope 1) and quadratic (Slope 2) behaviors. As shown, the KMeans−−, the KMeans−−* and the OPTICS-OF are fast and report linear scalability. The methods LOF, EMOutlier, and KNNOutlier are slightly slower, but they also present linear trends. Distinctly, the methods GLOSH, DBSCANOD, SilhouetteOD, SilhouetteOD*, OutRank S1/D, and OutRank S1/H are much slower and present quadratic scalability. Additionally, it is worth highlighting the results of KMeansOD and iForest. Note that the runtime of KMeansOD grows sublinearly in the plot. However, this result is biased, because ELKI’s optimized implementation of the KMeansOD speeds up the execution by avoiding distance computations through clever use of distance bounds and the triangle inequality (Hamerly 2010). The method iForest also appears to be sublinear in the plot, this time due to its subsampling approach. Note that, in theory, both the KMeansOD and the iForest should scale linearly, but the constants associated with a sublinear part of the execution seem to be much larger than those of the linear part for this data.

Figures 11b and 11c report the results for the 2-dimensional datasets with 5 and 10 clusters, respectively. Overall, all methods behave similarly to what was seen before, in Fig. 11a. In addition, we note that the curves of the plots are agglomerated into three groups, each corresponding to methods with similar behavior. The first group comprises of the methods iForest, KMeansOD, KMeans−−, KMeans−−*, OPTICS-OF, and LOF; they are the fastest and most scalable methods. The second group includes the methods EMOutlier, KNNOutlier, GLOSH, DBSCANOD, and SilhouetteOD; they provide ordinary results in terms of absolute runtime, however, KNNOutlier stands out by a better scalability behavior, which is the more interesting property (Kriegel et al. 2017). The third group has the slowest methods with empirical quadratic behavior, namely, the OutRank S1/D, the OutRank S1/H, and the SilhouetteOD*.Footnote 3

Figure 11d regards the 10-dimensional dataset with 2 clusters and outliers. We highlight that iForest maintained the sublinear behavior seen before, in the 2-dimensional data, which is due to sampling. The methods with linear behavior are KMeansOD, KMeans−−, KMeans−−*, and EMOutlier. However, EMOutlier has a runtime one order of magnitude larger than those of the other methods mentioned. Note that the runtime of EMOutlier is largely determined by the tolerance for convergence, and it could be reduced by allowing more tolerance. The remaining methods present a quadratic trend. The results in Figs. 11e and 11f regard the datasets with 5 and 10 clusters, respectively, and have patterns similar to those of Fig. 11d.

In summary, the impact in terms of runtime is evident for all methods when the cardinality, dimensionality and the number of clusters of a dataset increase. Hence, one must evaluate the pros and cons of every method for each particular application, because the most effective methods will not always present appropriate or even feasible scalability in large and complex data.

6 Discussion

The results of our study serve as a basis for discussing whether or not there is significant distinction between the clustering and the non-clustering-based methods regarding effectiveness, efficiency and ease of use in practice. They also allow us to compare the approaches used for clustering-based anomaly detection, including the k-means-based, the density-based, and the ensemble approaches. In the following we discuss our key findings regarding the five criteria evaluated:

  • C1 – Accuracy;

  • C2 – Resilience to data variation;

  • C3 – Resilience to parameter configuration;

  • C4 – Automatized parameter selection, and;

  • C5 – Scalability.

Let us first discuss the effectiveness of the methods based on the results presented in Sect. 5.1 – Accuracy. We consider the experimental results regarding the average values obtained from each method under distinct configuration of parameters because they better reflect real-world application scenarios. Overall, there is no evident distinction between the clustering and the non-clustering-based approaches. This is confirmed by the thick horizontal lines connecting most methods in the critical difference diagrams of Fig. 3, and also by the small differences in the average rank positions of the top performing methods in many cases. However, it is plausible to state that the k-means-based methods are generally placed in the top positions. Their underlying assumption – that is, assessing the degree of outlierness of a point by considering how close it is to a cluster or how likely it is to be a member of a cluster – highlights the rarity of the points potentially identifiable as anomalies.

Furthermore, as described in Sect. 5.2 – Resilience to Data Variation, the clustering-based methods are generally more resilient to data variation than the non-clustering based ones. Once again, the methods based on k-means are the best performers, which is particularly evident for the EMOutlier, the KMeans−− and the SilhouetteOD that stand out as the most resilient methods in both real and synthetic data. Looking again at Figs. 4, 5 and 6, it is clear that some methods achieve high values in the evaluation meassures. Nevertheless, these values reflect good results obtained from a few different datasets, and not necessarily good resilience. When evaluating the resilience to data variation, it is desired that a method succeeds in data with varying characteristics, which is expected to be necessary when identifying anomalies in distinct applications.

Moreover, as described in Sect. 5.3 – Resilience to Parameter Configuration, we could not notice significant distinction between the clustering and the non-clustering-based approaches when analyzing the resilience to the configuration of parameters. Nevertheless, if considering only the methods of the former approach, we note that the EMOutlier, the KMeansOD and the KMeans−− report higher resilience than the remaining methods, thus evidencing superiority of the k-means-based methods over the density-based and the ensemble ones. It is also worth highlighting the influence of “forced high resilience” on datasets with a high degree of difficulty. Both clustering and non-clustering-based methods experience this phenomenon. Furthermore, by revisiting the results of our “overall view” shown in Fig. 8, it is plausible to conclude that all methods strongly rely on a suitable choice of parameters when confronted with difficult datasets. We show that considering broad ranges of parameter values is critical in evaluating outlier detection methods to avoid misleading experimental results.

We also studied whether or not one can mitigate the exhaustive parameter search for clustering-based anomaly detectors by capitalizing on well-known measures of internal clustering quality. As shown in Sect. 5.4 – Automatized Parameter Selection, although this strategy cannot fully automatize the selection of parameter values, it may be an excellent alternative to automatically filter out inappropriate values that lead to poor effectiveness, hence reducing the number of possibilities to be considered in the exhaustive search and its factor of randomness. Distinctly, no equivalent automatized parameter selection strategy exists for the non-clustering-based methods, which commonly leads to the use of randomly (“blindly”) selected parameter values that are rarely ideal.

Finally, let us consider scalability. As shown in Sect. 5.5 – Scalability, the most scalable (and fastest) methods are those based on k-means, which may come from the fact that these methods form the clusters before attributing outlierness scores to each point. Alongside the k-means-based methods are the subsampling-based ones, such as iForest, which do not process the entire dataset and therefore cannot be fairly compared with the other methods regarding runtime. Also the other non-clustering-based methods are quite competitive in terms of runtime behavior. Nevertheless, it is rarely prudent to consider scalability as the sole criterion for choosing an anomaly detection strategy because the accuracy of the detection plays a crucial role in most applications.

Table 4 summarizes our findings. We evaluate the clustering-based approach and the non-clustering-based ones, and summarize our key findings in the table by indicating whether each of these two options surpasses (\(\mathbf {++}\)), marginally surpasses (\(\mathbf {+}\)), or is competitive (\(\mathbf {\equiv }\)) when compared with the other option regarding the five main criteria considered. Hence, it is plausible to conclude that the clustering-based methods present a competitive performance in general terms among the methods studied, and their best representatives are the ones based on k-means. Consequently, we argue that clustering-based anomaly detectors can be seen as genuinely competitive options capable of reaching similar (and even better) results than some of the most famous and commonly used algorithms of the state of the art.

Table 4 Summary of findings. We evaluate the clustering-based approach and the non-clustering-based ones considering criteria C1 to C5, and summarize our findings by indicating whether each of these two options surpasses (\(\mathbf {++}\)), marginally surpasses (\(\mathbf {+}\)), or is competitive (\(\mathbf {\equiv }\)) compared with the other
Full size table

7 Conclusion

This section concludes our study. We first summarize the work performed, the results obtained and the corresponding contributions. Then, we provide our outlook on the many opportunities for improvement brought to light through our endeavor to expand the knowledge about the clustering-based approach to detect anomalies.

7.1 Summary

In this work, we performed an extensive experimental and conceptual evaluation of 11 clustering-based outlier detection methods, and compared them against 3 of the most studied and used algorithms of the state of the art that employ distinct approaches. We presented a comprehensive analysis based on a collection of 46 real and synthetic datasets of diverse nature with up to 125, 000 points and 1, 555 dimensions, considering 4 evaluation measures of effectiveness and broad ranges of values used to configure the parameters of the algorithms. Specifically, our main contributions are:

  • C1 Accuracy evaluation We performed a comprehensive statistical analysis comparing the clustering and the non-clustering-based outlier detectors in terms of effectiveness.

  • C2 Resilience to data variation evaluation We conducted an extensive experimental study of the resilience of the methods when analyzing data of distinct nature.

  • C3 Resilience to parameter variation evaluation We conducted an extensive experimental study of the resilience of the methods to variation in their parameter configuration.

  • C4 Automatized parameter selection evaluation We analyzed the feasibility of filtering out parameter values inappropriate to outlier detectors automatically, by capitalizing on internal measures of clustering quality.

  • C5 Scalability evaluation We analyzed the scalability of outlier detectors on datasets with different dimensionality and different number of clusters to provide experimental evidence that help selecting a method based on its efficiency in handling large datasets.

To our knowledge, this work is the first attempt to analytically and empirically demonstrate the pros and cons of clustering-based approaches to anomaly detection. Our main goal was to find out whether or not the clustering-based methods are competitive in terms of efficiency, effectiveness and ability of being easy to use in practice. As we summarized in Table 4, our results demonstrate that they are indeed competitive. Hence, we argue that clustering-based approaches should be included as baselines in future benchmarking studies, especially k-means-based methods such as the KMeans−−. These methods often offer a competitive quality at a relatively low run time, besides several other benefits such as the possibility to capitalize on more mature evaluation measures, more developed subspace analysis for high-dimensional data and better explainability.

7.2 Outlook

We conclude our study by emphasizing that the field of clustering-based detection of outliers offers many opportunities for improvement.

An interesting benefit of clustering-based methods for outlier detection is the more developed research about clustering and clustering evaluation measures. Especially model selection methodology is more mature for clustering (Vendramin et al. 2010; Naldi et al. 2013; Jaskowiak et al. 2016; Iglesias et al. 2020; Jaskowiak et al. 2022) than for outlier detection (Marques et al. 2020, 2022, 2023; Ma et al. 2023), even though it is of course also for clustering far from trivial. Although our experiments could not confirm that the use of clusterings chosen by model selection would make good outlier detection results for clustering-based outlier detection methods more likely, we only tested two simple straightforward strategies and would not see our results as discouraging from the development of more refined methods.

An additional direction for future work is the analysis of high-dimensional data. It has been shown extensively in the literature (Kriegel et al. 2009b) that data of high dimensionality rarely form clusters in the full dimensional space; distinctly, the clusters often occur only in subspaces of lower dimensionality, which should be taken into account when detecting outliers because the points of these clusters must be distinguished from the true anomalies. Provided that the analysis of subspaces is also more mature for clustering (Agrawal et al. 1998; Aggarwal and Yu 2000; Moise et al. 2006; Achtert et al. 2007b, Achtert et al., Cordeiro et al. 2011, 2013) than for outlier detection (Kriegel et al. 2009a, 2012; Müller et al. 2010, 2011; Zimek et al. 2012), one promising future work would be to detect anomalies by capitalizing on the many subspace clustering algorithms available in the literature, thus following the ideas introduced by Müller et al. (2008) which were not much explored further afterwards.

Another interesting direction would be the further development of outlier detection methods for streaming data. Also in the scenario of streaming data, literature on methods for clustering are much more developed (de Andrade Silva et al. 2013; Silva et al. 2016; Mansalis et al. 2018; Zubaroglu and Atalay 2021; Aggarwal 2013, 2023) than for outlier detection (Keogh et al. 2005; Sadik and Gruenwald 2013; Boukerche et al. 2021; Iglesias Vázquez et al. 2023). Building upon clustering methods for streaming data for outlier detection seems a quite promising and under-researched idea.

Besides adaptations for streaming data, clustering-based methods would also more generally suggest means for algorithmic engineering for improving runtime or space requirements that are not available to the classic non-clustering-based methods. While the latter mostly rely on classic filter-refinement-approaches when considering top-n solutions (Orair et al. 2010) or indexing (sometimes combined with approximations) (Knorr and Ng 1998; Wang et al. 2011; Schubert et al. 2015b; Zimek et al. 2012; Okkels et al. 2024) for speeding up neighborhood queries, clustering-based solutions could build upon speed-up techniques for the underlying clustering, albeit often tailored for specific clustering methods (Elkan 2003; Hamerly 2010). However, there might also come some unnecessary algorithmic overhead with the clustering. Avoiding such overhead might have been part of the motivation for the development of non-clustering-based methods. Accordingly, the non-clustering-based methods showed overall good scalability in our experiments (Fig. 11), which, however, only demonstrates that there might be potential for algorithmic improvements in clustering-based methods.

Finally, resorting to clusters explicitly as normal data and qualifying outliers as not belonging to any cluster adds more possibilities to the portfolio of explainable outlier detection (Knorr and Ng 1999; Kriegel et al. 2012; Dang et al. 2014; Li et al. 2024).

Stimulating future research on clustering-based detectors of outliers was the primary goal behind our study, and we hope it will trigger new ideas and proposals from the research community.