Abstract
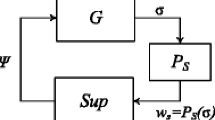
Given a finite state system with partial observers and for each observer, a regular set of trajectories which we call a secret, we consider the question whether the observers can ever find out that a trajectory of the system belongs to some secret. We search for a regular control on the system, enforcing the specified secrets on the observers, even though they have full knowledge of this control. We show that an optimal control always exists although it is generally not regular. We state sufficient conditions for computing a finite and optimal control of the system enforcing the concurrent secret as desired.
Similar content being viewed by others
References
Arnold A, Nivat M (1982) Comportements de processus. In: Actes du Colloque AFCET “Les mathématiques de l’informatique”, pp 35–68
Berstel J (1978) Transductions and context-free languages. Teubner
Bryans JW, Koutny M, Mazaré L, Ryan PYA (2006) Opacity generalised to transition systems. In: revised selected papers of the 3rd international workshop on formal aspects in security and trust (FAST 2005). LNCS, vol 3866. Newcastle upon Tyne, UK, Springer Verlag, pp 81–95
Eilenberg S (1974) Automata, languages and machines, vol A. Academic, New York
Ginzburg A (1968) Algebraic theory of automata. Academic, New York
Mazaré L (2004) Using unification for opacity properties. In: Proc. of the 4th IFIP WG1.7 Workshop on Issues in the Theory of Security (WITS’04), Barcelona, Spain, pp 165–176
Ramadge PJ, Wonham WM (1987a) Supervisory control of a class of discrete event processes. SIAM J Control Optim 25:206–230
Ramadge PJ, Wonham WM (1987b) On the supremal controllable language of a given language. SIAM J Control Optim 25:637–659
Tarski A (1955) A lattice-theoretical fixpoint theorem and its applications. Pacific J Math 5:285–309
Author information
Authors and Affiliations
Corresponding author
Additional information
The biographies and photos of the authors are not available.
Rights and permissions
About this article
Cite this article
Badouel, E., Bednarczyk, M., Borzyszkowski, A. et al. Concurrent Secrets. Discrete Event Dyn Syst 17, 425–446 (2007). https://doi.org/10.1007/s10626-007-0020-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10626-007-0020-5