Skip to main content

Advertisement

Springer Nature Link
Log in

Fault Diagnosis in Discrete Event Systems Modeled by Partially Observed Petri Nets

  • Published:
Discrete Event Dynamic Systems Aims and scope Submit manuscript

Abstract

In this paper, we study fault diagnosis in discrete event systems modeled by partially observed Petri nets, i.e., Petri nets equipped with sensors that allow observation of the number of tokens in some of the places and/or partial observation of the firing of some of the transitions. We assume that the Petri net model is accompanied by a (possibly implicit) description of the likelihood of each firing sequence. Faults are modeled as unobservable transitions and are divided into different types. Given an ordered sequence of observations from place and transition sensors, our goal is to calculate the belief (namely, the degree of confidence) regarding the occurrence of faults belonging to each type. To handle information from transition and place sensors in a unified manner, we transform a given partially observed Petri net into an equivalent (as far as state estimation and fault diagnosis is concerned) labeled Petri net (i.e., a Petri net with only transition sensors), and construct a translator that translates the sensing information from place and transition sensors into a sequence of labels in the equivalent labeled Petri net. Once this transformation is established, we focus on the computation of beliefs on faults in a given labeled Petri net and construct an online monitor that recursively produces these beliefs by tracking the existence of faulty transitions in execution paths that match the sequence of labels observed so far. Using the transformed labeled Petri net and the translated observation sequence, we can then compute the belief for each fault type in partially observed Petri nets in the same way as in labeled Petri nets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. Possible paths are sequences of transitions that are consistent with a given sequence of observations.

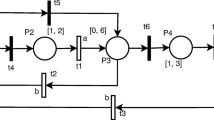
  2. To avoid confusion between Σ and Σ′, we define a new label a 1 instead of using the original label a.

  3. T − T o ′ is the set of transitions that will generate neither token changes nor an observable transition label; therefore, such transitions will be mapped to ε in the constructed labeled Petri net. In other words, T − T o ′ = T ε , where T ε is obtained from L′ in (G, Σ′, L′).

References

  • Aghasaryan A, Fabre E, Benveniste A, Boubour R, Jard C (1998) Fault detection and diagnosis in distributed systems: An approach by partially stochastic Petri nets. Discret Event Dyn Syst Theory Appl Categ 8:203–231

    Article  MATH  MathSciNet  Google Scholar 

  • Benveniste A, Fabre E, Haar S (2003a) Markov nets: Probabilistic models for distributed and concurrent systems. IEEE Trans Automat Contr 48:1936–1950

    Article  MathSciNet  Google Scholar 

  • Benveniste A, Fabre E, Haar S, Jard C (2003b) Diagnosis of asynchronous discrete-event systems: A net unfolding approach. IEEE Trans Automat Contr 48:714–727

    Article  MathSciNet  Google Scholar 

  • Cassandras CG, Lafortune S (2008) Introduction to discrete event systems (2nd Edition). Springer, New York

    MATH  Google Scholar 

  • Chung SL (2005) Diagnosing PN-based models with partial observable transitions. Int J Comput Integr Manuf 18:158–169

    Article  Google Scholar 

  • Esparza J, Nielsen M (1994) Decidability issues for Petri nets—a survey. Bull Eur Assoc Theor Comput Sci 52:245–262

    MATH  Google Scholar 

  • Genc S, Lafortune S (2007) Distributed diagnosis of place-bordered Petri nets. IEEE Trans Autom Sci Eng 4:206–219

    Article  Google Scholar 

  • Giua A, Seatzu C (2005) Fault detection for discrete event systems using Petri nets with unobservable transitions. In: 44th IEEE Conf. on Decision and Control, Seville, pp 6323–6328

  • Giua A, Corona D, Seatzu C (2005) State estimation of λ-free labeled Petri nets with contact-free nondeterministic transitions. Discret Event Dyn Syst Theory Appl Categ 15:85–108

    Article  MATH  MathSciNet  Google Scholar 

  • Giua A, Seatzu C, Corona C (2007) Marking estimation of Petri nets with silent transitions. IEEE Trans Automat Contr 52:1695–1699

    Article  MathSciNet  Google Scholar 

  • Hadjicostis CN, Verghese GC (1999) Monitoring discrete event systems using Petri net embeddings. In: Application and Theory of Petri Nets 1999 (Series Lecture Notes in Computer Science, vol. 1639), pp 188–207

  • Jiang S, Kumar R, Garcia HE (2002) Diagnosis of repeated failures in discrete event systems. In: 41st IEEE Conf. on Decision and Control, Las Vegas, pp 4000–4005

  • Lefebvre D, Delherm C (2007) Diagnosis of DES with Petri net models. IEEE Trans Automat Sci Eng 4:114–118

    Article  Google Scholar 

  • Li L, Ru Y, Hadjicostis CN (2006) Least-cost firing sequence estimation in labeled Petri nets. In: Proc. of 45th IEEE Conf. on Decision and Control, San Diego, pp 416–421

  • Murata T (1989) Petri nets: Properties, analysis and applications. Proc IEEE 77:541–580

    Article  Google Scholar 

  • Pearl J (1988) Probabilistic reasoning in intelligent systems: networks of plausible inference. Morgan Kaufmann, San Francisco

    Google Scholar 

  • Peterson JL (1981) Petri net theory and the modelling of systems. Prentice-Hall, New Jersey

    MATH  Google Scholar 

  • Ramadge PJ, Wonham WM (1989) The control of discrete event systems. Proc IEEE 77:81–98

    Article  Google Scholar 

  • Ramírez-Treviño A, Ruiz-Beltrán E, Rivera-Rangel I, López-Mellado E (2007) Online fault diagnosis of discrete event systems. a Petri net-based approach. IEEE Trans Automat Sci Eng 4:31–39

    Article  Google Scholar 

  • Ru Y, Hadjicostis CN (2009a) Bounds on the number of markings consistent with label observations in Petri nets. IEEE Trans Automat Sci Eng 6:334–344

    Article  Google Scholar 

  • Sampath M, Sengupta R, Lafortune S, Sinnamohideen K, Teneketzis D (1995) Diagnosability of discrete event systems. IEEE Trans Automat Contr 40:1555–1575

    Article  MATH  MathSciNet  Google Scholar 

  • Thorsley D, Teneketzis D (2005) Diagnosability of stochastic discrete-event systems. IEEE Trans Automat Contr 50:476–492

    Article  MathSciNet  Google Scholar 

  • Thorsley D, Yoo TS, Garcia HE (2008) Diagnosability of stochastic discrete-event systems under unreliable observations. In: Proc. of the 2008 American Control Conference, Seattle, pp 1158–1165

  • Ushio T, Onishi I, Okuda K (1998) Fault detection based on Petri net models with faulty behaviors. In: Proc. of IEEE Int. Conf. on Systems, Man, and Cybernetics, San Diego, pp 113–118

  • Wu Y, Hadjicostis CN (2005) Algebraic approaches for fault identification in discrete-event systems. IEEE Trans Automat Contr 50:2048–2053

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to thank anonymous reviewers for very helpful comments on the initial submission of this paper and an earlier conference paper that included some of these results.

Author information

Authors and Affiliations

  1. Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, USA

    Yu Ru & Christoforos N. Hadjicostis

  2. Department of Electrical and Computer Engineering, University of Cyprus, 75 Kallipoleos Ave, P.O.Box 20537, 1678, Nicosia, Cyprus

    Christoforos N. Hadjicostis

Authors
  1. Yu Ru
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Christoforos N. Hadjicostis
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yu Ru.

Additional information

This material is based upon work supported in part by the National Science Foundation under NSF ITR Award 0426831 and NSF CNS Award 0834409. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the authors and do not necessarily reflect the views of NSF. The research leading to these results has also received funding from the European Community’s Seventh Framework Programme (FP7/2007-2013) under grant agreements INFSO-ICT-223844 and PIRG02-GA-2007-224877.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ru, Y., Hadjicostis, C.N. Fault Diagnosis in Discrete Event Systems Modeled by Partially Observed Petri Nets. Discrete Event Dyn Syst 19, 551–575 (2009). https://doi.org/10.1007/s10626-009-0074-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10626-009-0074-7

Keywords