Abstract
Like many other service organizations, drop-in peer tutoring centers often struggle to determine the required number of qualified tutors necessary to meet learner expectations. Service work is largely a response to probabilistic calls for staff action and therefore difficult to forecast with precision. Moreover, forecasting models under long planning horizons often lack the complexity or specificity necessary to accurately predict flexible labor demand due to sparse availability of influential model inputs. This study builds upon the flexible demand literature by exploring the use of neural networks for labor demand forecasting for a drop-in peer tutoring center of a large university. Specifically, this study employs a neural network solution that includes a genetic algorithm to search for optimal solutions using evolutional processes. The proposed forecasting model outperforms traditional smoothing and extrapolation forecasting methods.



Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Change history
11 July 2019
The original version of this article unfortunately contained a mistake. The name of the last author was incorrectly spelled. The correct name of the last author is ���Brittaney Wheatley,��� which is now correctly spelled in this article.
References
Agarwal, A., Colak, S., & Erenguc, S. (2011). A Neurogenetic approach for the resource-constrained project scheduling problem. Computers & Operations Research, 38(1), 44–50.
Albright, S. C., & Winston, W. L. (2017). Business analytics: Data analysis and decision making (6th ed.). Boston: Cengage Learning.
Altay, A., Ozkant, O., & Kayakutlu, G. (2014). Prediction of aircraft failure times using artificial neural networks and genetic algorithms. Journal of Aircraft, 51(1), 47–53.
Armstrong, J. S. (1984). Forecasting by extrapolation: Conclusions from 25 years of research. Interfaces, 14(6), 52–66.
Armstrong, J. S. (1986). The ombudsman: Research on forecasting: A quarter-century review, 1960-1984. Interfaces, 16(1), 89–103.
Backer, L., Van Keer, H., Moerkerke, B., & Valcke, M. (2016). Examining evolutions in the adoption of metacognitive regulation in reciprocal peer tutoring groups. Metacognition and Learning, 11(2), 187–213.
Bard, J. F., Morton, D. P., & Yong Min, W. (2007). Workforce planning at USPS mail processing and distribution centers using stochastic optimization. Annals of Operations Research, 155(1), 51–78.
Billio, M., & Casarin, R. (2010). Identifying business cycle turning points with sequential Monte Carlo methods: An online and real-time application to the euro area. Journal of Forecasting, 29(1/2), 145–167.
Bolton, L. E. (2003). Stickier priors: The effects of nonanalytic versus analytic thinking in new product forecasting. Journal of Marketing Research (JMR), 40(1), 65–79.
Brahnam, S., Chuang, C.-F., Sexton, R. S., & Shih, F. Y. (2007a). Machine assessment of neonatal facial expressions of acute pain. Decision Support Systems, 43(4), 1242–1254.
Brahnam, S., Nanni, L., & Sexton, R. S. (2007b). Introduction to neonatal facial pain detection using common and advanced face classification techniques. In Yoshida H., Jain A., Ichalkaranje A., Jain L.C., Ichalkaranje N. (eds), Advanced computational intelligence paradigms in healthcare (pp. 225–239). Springer.
Camm, J. D., Cochran, J. J., M.J., F., Ohlmann, J. W., Anderson, D. R., Sweeney, D. J., & Williams, T. A. (2017). Essentials of Business Analytics (2 ed.). Boston: Cengage Learning. https://link.springer.com/chapter/10.1007%2F978-3-540-47527-9_9#citeas
Chase Jr, C. W. (1997). Selecting the Appropriate Forecasting Method. Journal of Business Forecasting Methods & Systems, 16, (3) p. 2.
Cooper, E. (2010). Tutoring center effectiveness: The effect of drop-in tutoring. Journal of College Reading and Learning, 40(2), 21–34.
DeFeo, D. J., Bonin, D., & der-Gobeille, M. O. (2017). Waiting and help-seeking in math tutoring exchanges. Journal of Developmental Education, 40(3), 14–22.
Defraeye, M., & Van Nieuwenhuyse, I. (2016). A branch-and-bound algorithm for shift scheduling with stochastic nonstationary demand. Computers & Operations Research, 65, 149–162.
Delen, D. (2015). Real-World Data Mining. In Upper Saddle River. New Jersey: Pearson Education, Inc.
Dikmen, B., & Küçükkocaoğlu, G. (2010). The detection of earnings manipulation: The three-phase cutting plane algorithm using mathematical programming. Journal of Forecasting, 29(5), 442–466.
Dorsey, R. E., & Johnson, J. D. (1997). Evolution of dynamic reconfigurable neural networks: Energy surface optimality using genetic algorithms. In D. Levine & W. Elsberry (Eds.), Optimality in Biological and Artificial Networks? (p. 185). Lawrence Erlbaum.
Dorsey, R. E., & Mayer, W. J. (1995). Genetic algorithms for estimation problems with multiple optima, nondifferentiability, and other irregular features. Journal of Business & Economic Statistics, 13(1), 53–66.
Dorsey, R. E., Johnson, J. D., & Mayer, W. J. (1994a). A genetic algorithm for the training of feedforward neural networks. In J. D. Johnson & A. B. Whinston (Eds.), Advances in artificial intelligence in economics, finance, and management (Vol. 1, pp. 93–111). Greenwich: JAI Press Inc.
Dorsey, R. E., Johnson, J. D., & Van Boening, M. V. (1994b). The use of artificial neural networks for estimation of decision surfaces in first Price sealed bid auctions. In W. W. Cooper & A. B. Whinston (Eds.), New direction in computational economics (pp. 19–40). Netherlands: Kluwer Academic Publishers.
Drago, A., Rheinheimer, D. C., & Detweiler, T. N. (2018). Effects of locus of control, academic self-efficacy, and tutoring on academic performance. Journal of College Student Retention: Research, Theory & Practice, 19(4), 433–451.
Drwal, M. (2018). Robust scheduling to minimize the weighted number of late jobs with interval due-date uncertainty. Computers & Operations Research, 91, 13–20.
Ernst, A. T., Jiang, H., Krishnamoorthy, M., Owens, B., & Sier, D. (2004a). An annotated bibliography of personnel scheduling and rostering. Annals of Operations Research, 127(1–4), 21–144.
Ernst, A. T., Jiang, H., Krishnamoorthy, M., & Sier, D. (2004b). Staff scheduling and rostering: A review of applications, methods and models. European Journal of Operational Research, 153(1), 3–27.
Fullmer, P. (2012). Assessment of tutoring Laboratories in a Learning Assistance Center. Journal of College Reading and Learning, 42(2), 67–89.
Gallard, A. J., Albritton, F., & Morgan, M. W. (2010). A comprehensive cost/benefit model: Developmental student success impact. Journal of Developmental Education, 34(1), 10–12.
Gerlaugh, K., Thompson, T., Boylan, H., & Davis, H. (2007). National Study of developmental education II: Baseline data for community colleges. Research in Developmental Education, 20(2), 1–4.
Gul, M., & Guneri, A. F. (2016). Planning the future of emergency departments: Forecasting Ed patient arrivals by using regression and neural network models. International Journal of Industrial Engineering, 23(2), 137–154.
Hao, G., Lai, K. K., & Tan, M. (2004). A neural network application in personnel scheduling. Annals of Operations Research, 128(1–4), 65–90.
Jiang, S., Chin, K.-S., Wang, L., Qu, G., & Tsui, K. L. (2017). Modified genetic algorithm-based feature selection combined with pre-trained deep neural network for demand forecasting in outpatient department. Expert Systems with Applications, 82, 216–230.
Kaboudan, M. A. (2003). Forecasting with computer-evolved model specifications: A genetic programming application. Computers & Operations Research, 30(11), 1661–1681.
Lian, G., Zhang, Y., Desai, J., Xing, Z., & Luo, X. (2018). Predicting taxi-out time at congested airports with optimization-based support vector regression methods. Mathematical Problems in Engineering, 1–11.
Liu, D., Li, H., Wang, W., & Zhou, C. (2015). Scenario forecast model of long term trends in rural labor transfer based on evolutionary games. Journal of Evolutionary Economics, 25(3), 649–670.
Mozo, A., Ordozgoiti, B., & Gómez-Canaval, S. (2018). Forecasting short-term data center network traffic load with convolutional neural networks. PLoS One, 13(2), e0191939.
Palma, W. (2016). Time Series Analysis. Hoboken. New Jersey: John Wiley & Sons, Inc.
Patuelli, R., Reggiani, A., Nijkamp, P., & Blien, U. (2006). New neural network methods for forecasting regional employment: An analysis of German labour markets. Spatial Economic Analysis, 1(1), 7–30.
Pazgal, A. I., & Radas, S. (2008). Comparison of customer balking and reneging behavior to queueing theory predictions: An experimental study. Computers & Operations Research, 35(8), 2537–2548.
Salcedo-Sanz, S., Xu, Y., & Yao, X. (2006). Hybrid meta-heuristics algorithms for task assignment in heterogeneous computing systems. Computers & Operations Research, 33(3), 820–835.
Schnaars, S. P., & Joseph Bavuso, R. (1986). Extrapolation models on very short-term forecasts. Journal of Business Research, 14(1), 27–36.
Sexton, R. S., Dorsey, R. E., & Johnson, J. D. (1998). Toward global optimization of neural networks: A comparison of the genetic algorithm and backpropagation. Decision Support Systems, 22(2), 171–185.
Sexton, R. S., Sriram, R. S., & Etheridge, H. (2003). Improving decision effectiveness of artificial neural networks: A modified genetic algorithm approach. Decision Sciences, 34(3), 421–442.
Sexton, R. S., Dorsey, R. E., & Sikander, N. A. (2004). Simultaneous optimization of neural network function and architecture algorithm. Decision Support Systems, 36(3), 283–296.
Sexton, R. S., McMurtrey, S., Michalopoulos, J. O., & Smith, A. M. (2005). Employee turnover: A neural network solution. Computers & Operations Research, 32(10), 2635–2651.
Sexton, R. S., McMurtrey, S., & Cleavenger, D. (2006). Knowledge discovery using a neural network simultaneous optimization algorithm on a real world classification problem. European Journal of Operational Research, 168(3), 1009–1018.
Shmueli, G., Bruce, P. C., Yahav, I., Patel, N. R., & Lichtendahl, K. C., Jr. (2018). Data Mining for Business Analytics. Hoboken: John Wiley & Sons, Inc.
Stellwagen, E., & Tashman, L. E. N. (2013). ARIMA: The models of box and Jenkins. Foresight: The International Journal of Applied Forecasting, 30, 28–33.
Tabachnick, B. G., & Fidell, L. S. (1983). Using multivariate statistics. New York: Harper and Row.
Tang, Q., Wilson, G. R., & Perevalov, E. (2008). An approximation manpower planning model for after-sales field service support. Computers & Operations Research, 35(11), 3479–3488.
Van den Bergh, J., Beliën, J., De Bruecker, P., Demeulemeester, E., & De Boeck, L. (2013). Personnel scheduling: A literature review. European Journal of Operational Research, 226(3), 367–385.
van den Oetelaar, W. F. J. M., van Stel, H. F., van Rhenen, W., Stellato, R. K., & Grolman, W. (2018). Mapping nurses’ activities in surgical hospital wards: A time study. PLoS One, 13(4), 1–18.
Wen-Ya, W., & Gupta, D. (2014). Nurse absenteeism and staffing strategies for hospital inpatient units. Manufacturing & Service Operations Management, 16(3), 439–454.
Yi, Y., Yanhua, C., Jun, S., Mingfei, L., Caihong, L., & Lian, L. (2016). An improved Grey neural network forecasting method based on genetic algorithm for oil consumption of China. Journal of Renewable & Sustainable Energy, 8(2).
Zeng, J. (2017). Forecasting aggregates with disaggregate variables: Does boosting help to select the Most relevant predictors? Journal of Forecasting, 36(1), 74–90.
Zhou, L., Zhao, P., Wu, D., Cheng, C., & Huang, H. (2018). Time Series Model for Forecasting the Number of New Admission Inpatients. BMC Medical Informatics & Decision Making, 18(1) N.PAG-N.PAG.
Zolfaghari, S., El Bouri, A., Namiranian, B., & Quan, V. (2007). Heuristics for large scale labour scheduling problems in retail sector. INFOR, 45(3), 111–122.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original version of this article was revised: The original version of this article unfortunately contained a mistake. The name of the last author was incorrectly spelled. The correct name of the last author is “Brittaney Wheatley,” which is now correctly spelled in this article.
Appendix 1 – Technical overview of the NNSOA
Appendix 1 – Technical overview of the NNSOA
This section provides a technical overview of the Neural Network Simultaneous Optimization Algorithm (NNSOA) used in this study. The NNSOA first determines the appropriate number of hidden nodes for the neural network. Starting with two hidden nodes, the neural network is trained for 1000 generations and the best solution is saved. An additional hidden node is inserted into the best solution and trained for another 1000 generations. The best solution from the previous architecture is brought into the next architecture by setting the weights of the additional node to zero in order to preserve previous learning. The remaining solutions of the new neural network are reinitialized using a different random seed for drawing initial weights. The process of adding new hidden nodes and retraining continues until the new hidden node fails to improve overall performance. At this point the initial structure of the neural network is set.
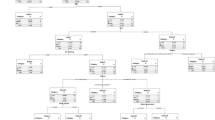
It has been shown that a variety of neural network structures will reduce to the same equivalent structure (Dorsey et al. 1994a; Dorsey et al. 1994b). The NNSOA next follows the genetic algorithm logic as shown in Fig. 4 to determine the most parsimonious set of inputs for the model. It first builds a population of 12 solutions by modifying the input and output weights of the neural network. The input weights are randomly drawn from a uniform probability distribution [−1,1]. The output weights are determined by ordinary least squares, which prior research has found most effective and efficient (Dorsey et al. 1994a; Sexton et al. 1998; Sexton et al. 2003). These 12 solutions make up the first generation. The algorithm next creates a series of 10,000 successive populations, each a genetically modified version of the previous.
At the beginning of each iteration all solutions of the current generation are individually evaluated by an objective function based on the sum of squares error (SSE). The function rewards parsimony by penalizing for each non-zero weight in the solution multiplied by the solution’s root mean square error (RMSE). The objective function is presented in eq. 3 below.
where:
- N:
-
the number of observations in the solution
- O:
-
the observed value of the dependent variable
- \( \hat{O} \) :
-
the estimated value of the dependent variable
- C:
-
the number of non-zero weights in the solution
The probability of a solution being redrawn in the next generation is determined by eq. 4. A next generation of 12 solutions is then randomly drawn with replacement from the current generation (i.e. reproduction). Duplication is allowed. Probabilities assigned in the evaluation step ensure that better solutions are more likely than poor solutions to appear in the next generation. In this way, traits that favor the objective function will reproduce and thrive in future generations, while weaker traits will die out over time.
where:
- E:
-
objective value of a given solution
- Emax:
-
maximum objective value of the current population
The 12 solutions of the next generation are then randomly organized into mating pairs. A random number is drawn from a uniform distribution [−1,1] for each pair. Each weight in the mating pair that is numerically less than the random number is switched for the weight in the same position of the mating solution. This crossover creates two new solutions, each with some parameters (weights) from each parent solution. Finally, each weight in each of the 12 solutions may receive additional adjustment (i.e. mutation). Each weight has a 5% chance for replacement by a randomly drawn value from the entire weight space. Searching the entire weight space enhances the algorithm’s ability to find global solutions. After 70% of specified generations are processed, convergence is enhanced by varying each mutation by a small random amount. The size of the random amount decreases with each subsequent generation. Once the specified number of generations have processed (10,000 for this study) the best solution is selected from the last generation according to the same objective function of the evaluation step.
Rights and permissions
About this article
Cite this article
Brattin, R., Sexton, R.S., Yin, W. et al. A neural network solution for forecasting labor demand of drop-in peer tutoring centers with long planning horizons. Educ Inf Technol 24, 3501–3522 (2019). https://doi.org/10.1007/s10639-019-09939-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10639-019-09939-7