Optimal contract design for live streaming shopping in a manufacturer–retailer–streamer supply chain

Abstract

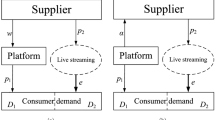
This study considers a manufacturer–retailer–streamer supply chain, in which the retailer first purchases products from a manufacturer and then sells them to consumers through a streamer. In the live streaming context, the retailer usually cooperates with the streamer by providing three different contracts: only a commission of the sale (OC), only a fixed fee (OF), and a commission of the sale and fixed fee (CF). Therefore, this study develops a theoretical model to investigate the effects of these three contracts on supply chain members’ optimal decisions and profits. The following results were obtained: (1) the retailer prefers an OC contract with a high-ability streamer, and the manufacturer benefits from this contract. Additionally, the manufacturer, retailer, and high-ability streamer can achieve a win–win–win outcome in certain cases. Furthermore, the retailer is willing to sign an OC contract with a low-ability streamer when the fixed fee of the OF contract is high. (2) The retailer prefers to cooperate with a low-ability streamer through an OF contract when the fixed fee is low. (3) The CF contract is the most profitable alternative for the retailer when the total commission rate is low and the fixed fee is medium.

Appendix

1.1 Proof of equilibrium solutions in Table 2

Under model OC

The retailer’s profit under the OC contract is:

$$\begin{array}{c}{\pi }_{r}^{OC}=\left({p}^{OC}-{w}^{OC}-r\right){D}^{OC}\\ =\left({p}^{OC}-{w}^{OC}-r\right)\left(1-{p}^{OC}+b{e}^{OC}\right)\end{array}$$

The first and second derivatives of ${\pi }_{r}^{OC}$ regarding ${p}^{OC}$ are $\frac{d{\pi }_{r}^{OC}}{d{p}^{OC}}=b{e}^{OC}+r+{w}^{OC}-2{p}^{OC}+1$ and $\frac{{d}^{2}{\pi }_{r}^{OC}}{d{p}^{{2}_{OC}}}=-2$, respectively.

Since $\frac{{d}^{2}{\pi }_{r}^{OC}}{d{p}^{{2}_{OC}}}=-2<0$, the retailer’s profit under the OC contract is concave in ${p}^{OC}$.

The streamer’s profit under the OC contract is:

$${\pi }_{s}^{OC}=r\left(1-{p}^{OC}+b{e}^{OC}\right)-\frac{c{{e}^{OC}}^{2}}{2}+s{e}^{OC}$$

The first and second derivatives of ${\pi }_{s}^{OC}$ regarding ${e}^{OC}$ are $\frac{d{\pi }_{s}^{OC}}{d{e}^{OC}}=br-c{e}^{OC}+s$ and $\frac{{d}^{2}{\pi }_{s}^{OC}}{d{e}^{{2}_{OC}}}=-c$, respectively.

Since $\frac{{d}^{2}{\pi }_{s}^{OC}}{d{e}^{{2}_{OC}}}=-c<0$, the streamer’s profit under the OC contract is concave in ${e}^{OC}$.

Thus, by solving $\frac{d{\pi }_{r}^{OC}}{d{p}^{OC}}=0$ and $\frac{d{\pi }_{s}^{OC}}{d{e}^{OC}}=0$ simultaneously, we have:

$${e}^{OC}=(br+s)/c$$

$${p}^{OC}=({b}^{2}r+bs+cr+c{w}^{OC}+c)/2c$$

Through backward induction, we substitute ${p}^{OC}$ and ${e}^{OC}$ into the manufacturer’s profit—that is, ${\pi }_{m}^{OC}={w}^{OC}(1-{p}^{OC}+b{e}^{OC})$. We have ${\pi }_{m}^{OC}={w}^{OC}(b\left(br+s\right)/c-({b}^{2}r+bs+cr+c{w}^{OC}+c)/2c+1$.

The first and second derivatives of ${\pi }_{m}^{OC}$ with respect to ${w}^{OC}$ are $\frac{d{\pi }_{m}^{OC}}{d{w}^{OC}}=b\left(br+s\right)/c-({b}^{2}r+bs+cr+c{w}^{OC}+c)/2c+1-{w}^{OC}/2$ and $\frac{{d}^{2}{\pi }_{m}^{OC}}{d{w}^{{2}_{OC}}}=-1<0$, respectively.

Thus, by solving $\frac{d{\pi }_{m}^{OC}}{d{w}^{OC}}=0$, we have ${w}^{OC*}=({b}^{2}r+bs-cr+c)/2c$. Next, we substitute ${w}^{OC*}$ with ${p}^{OC}=({b}^{2}r+bs+cr+c{w}^{OC}+c)/2c$. Thus, we obtain ${p}^{OC*}=(r+3)c+3{b}^{2}r+3bs/4c$.

Under model OF.

The retailer’s profit under the OF contract is:

$$\begin{array}{c}{\pi }_{r}^{OF}=\left({p}^{OF}-{w}^{OF}\right){D}^{OF}-k\\ =\left({p}^{OF}-{w}^{OF}\right)\left(1-{p}^{OF}+b{e}^{OF}\right)-k\end{array}$$

The first and second derivatives of ${\pi }_{r}^{OF}$ regarding ${p}^{OF}$ are $\frac{d{\pi }_{r}^{OF}}{d{p}^{OF}}=b{e}^{OF}+{w}^{OF}-2{p}^{OF}+1$ and $\frac{{d}^{2}{\pi }_{r}^{OF}}{d{p}^{{2}_{OF}}}=-2$, respectively.

Since $\frac{{d}^{2}{\pi }_{r}^{OF}}{d{p}^{{2}_{OF}}}=-2<0$, the retailer’s profit under the OF contract is concave in ${p}^{OF}$.

The streamer’s profit under the OF contract is:

$${\pi }_{s}^{OF}=k-\frac{c{{e}^{OF}}^{2}}{2}+s{e}^{OF}$$

The first and second derivatives of ${\pi }_{s}^{OF}$ regarding ${e}^{OF}$ are $\frac{d{\pi }_{s}^{OF}}{d{e}^{OF}}=-c{e}^{OF}+s$ and $\frac{{d}^{2}{\pi }_{s}^{OF}}{d{e}^{{2}_{OF}}}=-c$, respectively.

Since $\frac{{d}^{2}{\pi }_{s}^{OF}}{d{e}^{{2}_{OF}}}=-c<0$, the streamer’s profit under OF contract is concave in ${e}^{OF}$.

Thus, by solving $\frac{d{\pi }_{r}^{OF}}{d{p}^{OF}}=0$ and $\frac{d{\pi }_{s}^{OF}}{d{e}^{OF}}=0$ simultaneously, we have:

$${e}^{OF}=s/c$$

$${p}^{OF}=(bs+c{w}^{OF}+c)/2c$$

Using backward induction, we substitute ${p}^{OF}$ and ${e}^{OF}$ into the manufacturer’s profit, that is, ${\pi }_{m}^{OF}={w}^{OF}(1-{p}^{OF}+b{e}^{OF})$. We obtain ${\pi }_{m}^{OF}={w}^{OF}\left(bs-c{w}^{OF}+c\right)/2c$.

The first and second derivatives of ${\pi }_{m}^{OF}$ regarding ${w}^{OF}$ are $\frac{d{\pi }_{m}^{OF}}{d{w}^{OF}}=(bs-c{w}^{OF}+c)/2c-{w}^{OF}/2$ and $\frac{{d}^{2}{\pi }_{m}^{OF}}{d{w}^{{2}_{OF}}}=-1<0$, respectively.

Thus, by solving $\frac{d{\pi }_{m}^{OF}}{d{w}^{OF}}=0$, we have ${w}^{OF}=(bs+c)/2c$. Next, we substitute ${w}^{OF*}$ into ${p}^{OF}=(bs+c{w}^{OF}+c)/2c$. Thus, we can obtain ${p}^{OF*}=(3c+3bs)/4c$.

Under model CF.

The retailer’s profit under the CF contract is:

$$\begin{array}{c}{\pi }_{r}^{CF}=\left({p}^{CF}-{w}^{CF}-\beta r\right){D}^{CF}-\alpha k\\ =\left({p}^{CF}-{w}^{CF}-\beta r\right)\left(1-{p}^{CF}+b{e}^{CF}\right)-\alpha k\end{array}$$

The first and second derivatives of ${\pi }_{r}^{CF}$ regarding ${p}^{CF}$ are $\frac{d{\pi }_{r}^{CF}}{d{p}^{CF}}=b{e}^{CF}+\beta r+{w}^{CF}-2{p}^{CF}+1$ and $\frac{{d}^{2}{\pi }_{r}^{CF}}{d{p}^{{2}_{CF}}}=-2$, respectively.

Since $\frac{{d}^{2}{\pi }_{r}^{CF}}{d{p}^{{2}_{CF}}}=-2<0$, the retailer’s profit under the CF contract is concave in ${p}^{CF}$.

The streamer’s profit under the CF contract is:

$${\pi }_{s}^{CF}=\left(1-{p}^{CF}+b{e}^{CF}\right)\beta r+\alpha k-\frac{c{{e}^{CF}}^{2}}{2}+s{e}^{CF}$$

The first and second derivatives of ${\pi }_{s}^{CF}$ regarding ${e}^{CF}$ are $\frac{d{\pi }_{s}^{CF}}{d{e}^{CF}}=b\beta r-c{e}^{OF}+s$ and $\frac{{d}^{2}{\pi }_{s}^{CF}}{d{e}^{{2}_{CF}}}=-c$, respectively.

Since $\frac{{d}^{2}{\pi }_{s}^{CF}}{d{e}^{{2}_{CF}}}=-c<0$, the streamer’s profit under the CF contract is concave in ${e}^{CF}$.

Thus, by solving $\frac{d{\pi }_{r}^{CF}}{d{p}^{CF}}=0$ and $\frac{d{\pi }_{s}^{CF}}{d{e}^{CF}}=0$ simultaneously, we have:

$${e}^{CF}=(b\beta r+s)/c$$

$${p}^{CF}=\left({b}^{2}\beta r+\beta cr+bs+c{w}^{OF}+c\right)/2c$$

Using backward induction, we substitute ${p}^{CF}$ and ${e}^{CF}$ into the manufacturer’s profit—that is, ${\pi }_{m}^{CF}={w}^{CF}(1-{p}^{CF}+b{e}^{CF})$. We have ${\pi }_{m}^{CF}={w}^{CF}(b\left(b\beta r+s\right)/c-({b}^{2}\beta r+\beta cr+bs+c{w}^{CF}+c)/2c+1$.

The first and second derivatives of ${\pi }_{m}^{CF}$ for ${w}^{CF}$ are $\frac{d{\pi }_{m}^{CF}}{d{w}^{CF}}=b\left(b\beta r+s\right)/c-({b}^{2}\beta r+\beta cr+bs+c{w}^{CF}+c)/2c+1-{w}^{CF}/2$ and $\frac{{d}^{2}{\pi }_{m}^{CF}}{d{w}^{{2}_{CF}}}=-1<0$, respectively.

Thus, by solving $\frac{d{\pi }_{m}^{CF}}{d{w}^{OF}}=0$, we obtain ${w}^{CF}=(r({b}^{2}-c)\beta +bs+c)/2c$. Next, we substitute ${w}^{CF*}$ with ${p}^{CF}=\left({b}^{2}\beta r+\beta cr+bs+c{w}^{OF}+c\right)/2c$. Thus, we obtain ${p}^{CF*}=(\beta r+3)c+3{b}^{2}\beta r+3bs)/4c$.

1.2 Proof of proposition 1

In accordance with the optimal streamer’s effort, we list the wholesale and product prices under different contracts in Table 2.

Since ${e}^{CF*}-{e}^{OF*}=b\beta r/c>0$ and ${e}^{OC*}-{e}^{CF*}=b\left(1-\beta \right)r/c>0$, we can directly derive, ${e}^{CF*}>{e}^{OF*}$ and ${e}^{OC*}>{e}^{CF*}$. Thus, ${e}^{OF*}<{e}^{CF*}<{e}^{OC*}$.

Since ${p}^{CF*}-{p}^{OF*}=(c\beta r+3{b}^{2}\beta r)/4c>0$ and ${p}^{OC*}-{p}^{CF*}=(r\left(1-\beta \right)c+3{b}^{2}(1-\beta )r)/4c>0$, we can directly derive, ${p}^{CF*}>{p}^{OF*}$ and ${p}^{OC*}>{p}^{CF*}$. Therefore, ${p}^{OF*}<{p}^{CF*}<{p}^{OC*}$.

As before, considering ${w}^{OF*}-{w}^{CF*}=r(c-{b}^{2})\beta /2c$, if $c<{b}^{2}$, we have ${w}^{OF*}-{w}^{CF*}<0$; otherwise, ${w}^{OF*}-{w}^{CF*}>0$.

Considering ${w}^{OF*}-{w}^{OC*}=r(c-{b}^{2})/2c$, if $c<{b}^{2}$, we have ${w}^{OF*}-{w}^{OC*}<0$; otherwise, ${w}^{OF*}-{w}^{OC*}>0$.

Considering ${w}^{CF*}-{w}^{OC*}=r\left(1-\beta \right)(c-{b}^{2})/2c$, if $c<{b}^{2}$, we have ${w}^{CF*}-{w}^{OC*}<0$; otherwise, ${w}^{CF*}-{w}^{OC*}>0$.

To summarize, given that $c<{b}^{2}$, we have ${w}^{OF*}<{w}^{CF*}<{w}^{OC*}$; otherwise, we have ${w}^{OF*}>{w}^{CF*}>{w}^{OC*}$.

1.3 Proof of proposition 2

Considering ${D}^{OF*}-{D}^{CF*}=r(c-{b}^{2})\beta /4c$, if $c<{b}^{2}$, we have ${D}^{OF*}-{D}^{CF*}<0$; otherwise, ${D}^{OF*}-{D}^{CF*}>0$.

Considering ${D}^{OF*}-{D}^{OC*}=r(c-{b}^{2})/4c$, if $c<{b}^{2}$, we have ${D}^{OF*}-{D}^{OC*}<0$; otherwise, ${D}^{OF*}-{D}^{OC*}>0$.

Considering ${D}^{CF*}-{D}^{OC*}=r\left(1-\beta \right)(c-{b}^{2})/4c$, if $c<{b}^{2}$, we have ${D}^{CF*}-{D}^{OC*}<0$; otherwise, ${D}^{CF*}-{D}^{OC*}>0$.

To summarize, given that $c<{b}^{2}$, we have ${D}^{CF*}<{D}^{CF*}<{D}^{OC*}$; otherwise, we have ${D}^{CF*}>{D}^{CF*}>{D}^{OC*}$.

1.4 Proof of proposition 3

Let ${k}_{OF-OC}$ denote the fixed-fee cut-off point for the retailer under OF and OC contracts. We set ${\pi }_{r}^{OF*}-{\pi }_{r}^{OC*}=0$ to derive ${k}_{OF-OC}=\left(\left({b}^{2}r+2bs-c\left(r-2\right)\right)\left(c-{b}^{2}\right)r\right)/16{c}^{2}$. If $k<{k}_{OF-OC}$, we have ${\pi }_{r}^{OF*}>{\pi }_{r}^{OC*}$; otherwise, we have ${\pi }_{r}^{OF*}<{\pi }_{r}^{OC*}$.

Let ${k}_{CF-OF}$ denote the fixed fee cut-off point for the retailer under CF and OF contracts. We set ${\pi }_{r}^{CF*}-{\pi }_{r}^{OC*}=0$ to derive ${k}_{CF-OF}=\left(\left(r\left({b}^{2}-c\right)\beta +2bs+2c\right)\beta \left(c-{b}^{2}\right)r\right)/16{c}^{2}\left(1-\alpha \right)$. If $k>{k}_{CF-OF}$, we have ${\pi }_{r}^{CF*}>{\pi }_{r}^{OF*}$; otherwise, we have ${\pi }_{r}^{CF*}<{\pi }_{r}^{OF*}$.

Let ${k}_{CF-OR}$ denote the fixed-fee cut-off point for the retailer under CF and OC contracts. We set ${\pi }_{r}^{CF*}-{\pi }_{r}^{OC*}=0$ to derive ${k}_{CF-OC}=((\left(-r\beta -r+2\right)c+\left(r\left(\beta +1\right)b+2s\right)b)\left(1-\beta \right)\left(c-{b}^{2}\right)r)/16{c}^{2}$. If $k<{k}_{CF-OC}$, we have ${\pi }_{r}^{CF*}>{\pi }_{r}^{OC*}$; otherwise, we have ${\pi }_{r}^{CF*}<{\pi }_{r}^{OC*}$.

When $c<{b}^{2}$, we have ${k}_{OF-OC}=\left(\left({b}^{2}r+2bs-c\left(r-2\right)\right)\left(c-{b}^{2}\right)r\right)/16{c}^{2}<0$, ${k}_{CF-OF}=\left(\left(r\left({b}^{2}-c\right)\beta +2bs+2c\right)\beta \left(c-{b}^{2}\right)r\right)/16{c}^{2}\left(1-\alpha \right)<0$, and ${k}_{CF-OC}=((\left(-r\beta -r+2\right)c+\left(r\left(\beta +1\right)b+2s\right)b)\left(1-\beta \right)\left(c-{b}^{2}\right)r)/16{c}^{2}<0$. Since the fixed fee is positive, we can derive $\forall k>0>{k}_{OF-OC}$ $\forall k>0>{k}_{CF-OF}$ And $\forall k>0>{k}_{CF-OR}$. Thus, when $c<{b}^{2}$, we can derive ${\pi }_{r}^{OC*}>{\pi }_{r}^{CF*}>{\pi }_{r}^{OF*}$.

For $c-{b}^{2}>0$. To study the effects of the commission of sale $r$ and fixed fee $k$ on the retailer’s profit, we set ${k}_{CF-OF}-{k}_{CF-OC}=0$, ${k}_{OF-OC}-{k}_{CF-OF}=0$, and ${k}_{CF-OC}-{k}_{CF-OF}=0$, respectively. For any formula, we can obtain two roots for $r$—${r}_{0}=0$ and ${r}_{1}=2\left(\beta +\alpha -1\right)\left(bs+c\right)/\left(\left({\beta }^{2}+\alpha -1\right)\left(c-{b}^{2}\right)\right)$. On the one hand, if $\beta +\alpha -1>0$ and ${\beta }^{2}+\alpha -1>0$, we have ${r}_{1}>1$. The second derivative of ${k}_{RF-OF}-{k}_{RF-OR}$ with respect to $r$ is ${\partial }^{2}\left({k}_{CF-OF}-{k}_{CF-OC}\right)/\partial {r}^{2}=\left({\beta }^{2}+\alpha -1\right){\left({b}^{2}-c\right)}^{2}/\left(16\alpha {c}^{2}\left(1-\alpha \right)\right)>0$. We can derive that ${k}_{CF-OF}>{k}_{CF-OC}$. ${\pi }_{r}^{CF}>max {(\pi }_{r}^{OF},{\pi }_{r}^{OC})$ only if ${k}_{CF-OF}<k<{k}_{CF-OC}$. Any $k$ cannot satisfy the range; therefore, we can derive ${\pi }_{r}^{CF}<max {(\pi }_{r}^{OF},{\pi }_{r}^{OC})$.

On the other hand, we set $\beta +\alpha -1>0$ and ${\beta }^{2}+\alpha -1<0$ to derive ${r}_{1}<0$ and ${\partial }^{2}\left({k}_{CF-OF}-{k}_{CF-OC}\right)/\partial {r}^{2}=\left({\beta }^{2}+\alpha -1\right){\left({b}^{2}-c\right)}^{2}/\left(16\alpha {c}^{2}\left(1-\alpha \right)\right)<0$; we also derive ${\pi }_{r}^{CF}<max {(\pi }_{r}^{OF},{\pi }_{r}^{OC})$. Therefore, when $c-{b}^{2}>0$ and $\beta +\alpha -1>0$, we have ${\pi }_{r}^{CF}<max {(\pi }_{r}^{OF},{\pi }_{r}^{OC})$.

If $\beta +\alpha -1<0$ and $\beta \in (\mathrm{0,1})$, ${\beta }^{2}+\alpha -1<0$; we have ${r}_{1}>1$ ${\partial }^{2}\left({k}_{CF-OC}-{k}_{OF-OC}\right)/\partial {r}^{2}=\left({\beta }^{2}+\alpha -1\right){\left({b}^{2}-c\right)}^{2}/\left(16\alpha {c}^{2}\right)<0$; we can derive that ${\pi }_{r}^{OC}$ outperforms both ${\pi }_{r}^{CF}$ and ${\pi }_{r}^{OF}$, if $k>{k}_{CF-OC}$. Similarly, propositions 1(iii), (b), and (c) can be proved.

1.5 Proof of proposition 4

Let ${k}_{OF-OC}^{^{\prime}}$ denote the fixed fee cut-off point for the streamer under OF and OC contracts. We set ${\pi }_{s}^{OF*}-{\pi }_{s}^{OC*}=0$ to obtain ${k}_{OF-OC}^{^{\prime}}=r\left(-{b}^{2}r+bs-cr+c\right)/(4c)$. If $k>{k}_{OF-OC}^{^{\prime}}$, we have ${\pi }_{s}^{OF*}>{\pi }_{s}^{OC*}$; otherwise, we have ${\pi }_{s}^{OF*}<{\pi }_{s}^{OC*}$.

Let ${k}_{CF-OF}^{^{\prime}}$ denote the fixed fee cut-off point for the retailer under CF and OF contracts. We set ${\pi }_{s}^{CF*}-{\pi }_{s}^{OF*}=0$ to obtain ${k}_{CF-OF}^{^{\prime}}=\beta r\left(-r\left({b}^{2}+c\right)\beta +bs+c\right)/\left(4c(1-\alpha )\right)$. If $k<{k}_{CF-OF}^{^{\prime}}$, we have ${\pi }_{s}^{CF*}>{\pi }_{s}^{OF*}$; otherwise, we have ${\pi }_{s}^{CF*}<{\pi }_{s}^{OF*}$.

Let ${k}_{CF-OC}^{^{\prime}}$ denote the fixed-fee cut-off point for the retailer under CF and OC contracts. We set ${\pi }_{s}^{CF*}-{\pi }_{s}^{OC*}=0$ to obtain ${k}_{CF-OC}^{^{\prime}}=(1-\beta )r\left(-r\left({b}^{2}+c\right)(\beta +1)+bs+c\right)/4c\alpha$. If $k>{k}_{CF-OC}^{^{\prime}}$, we have ${\pi }_{s}^{CF*}>{\pi }_{s}^{OC*}$; otherwise, we have ${\pi }_{s}^{CF*}<{\pi }_{s}^{OC*}$.

To study the effects of the commission of sale $r$ and fixed fee $k$ on the streamer’s profit, we set ${k}_{OF-OC}^{^{\prime}}-{k}_{CF-OC}^{^{\prime}}=0$; ${k}_{OF-OC}^{^{\prime}}-{k}_{CF-OF}^{^{\prime}}=0$; and ${k}_{CF-OC}^{^{\prime}}-{k}_{CF-OF}^{^{\prime}}=0$, respectively. For any formula, we can obtain two roots for $r$—${r}_{0}=0$ and ${r}_{2}=(\beta +\alpha -1)\left(bs+c\right)/(({\beta }^{2}+\alpha -1)({b}^{2}+c))$. For $\beta +\alpha -1>0$ and ${\beta }^{2}+\alpha -1>0$, we have ${r}_{2}>0$. The second derivative of ${k}_{CF-OC}^{^{\prime}}-{k}_{CF-OF}^{^{\prime}}$ with respect to $r$ is ${\partial }^{2}\left({k}_{CF-OC}^{^{\prime}}-{k}_{CF-OF}^{^{\prime}}\right)/\partial {r}^{2}=\left({\beta }^{2}+\alpha -1\right)({b}^{2}+c)/\left(4\alpha c(\alpha -1)\right)<0$. Using the same method, the streamer’s profit relationship is that ${\pi }_{s}^{OR}>({\pi }_{s}^{RF}, {\pi }_{s}^{OF})$, if $k<{k}_{CF-OC}^{^{\prime}}<{k}_{OF-OC}^{^{\prime}}$; if $k>{k}_{CF-OF}^{^{\prime}}$, ${\pi }_{s}^{OF}>{(\pi }_{s}^{CF}, {\pi }_{s}^{OC})$; if ${k}_{CF-OC}^{^{\prime}}<k<{k}_{CF-OF}^{^{\prime}}$, ${\pi }_{s}^{CF}>({\pi }_{s}^{OF}, {\pi }_{s}^{OC})$.

If $\beta +\alpha -1<0$ and $\beta \in (\mathrm{0,1})$, ${\beta }^{2}+\alpha -1<0$. Under this condition, if ${r}_{2}>1$, i.e., $s>{s}_{1}$, we have ${\partial }^{2}\left({k}_{CF-OC}^{^{\prime}}-{k}_{CF-OF}^{^{\prime}}\right)/\partial {r}^{2}=\left({\beta }^{2}+\alpha -1\right)({b}^{2}+c)/\left(4\alpha c(\alpha -1)\right)>0$. Consequently, ${k}_{CF-OF}<{k}_{CF-OC}$, which cannot satisfy ${k}_{CF-OC}<k<{k}_{CF-OF}$. Hence, ${\pi }_{r}^{CF}<max {(\pi }_{r}^{OF},{\pi }_{r}^{OC})$; furthermore, against this background, if ${r}_{2}<r<1$ and $0<{r}_{2}<1$, i.e., $0<s<{s}_{1}$, we have the same result as proposition 2(i). If $0<r<{r}_{2}$ and $0<{r}_{2}<1$, we can derive ${k}_{CF-OF}<{k}_{CF-OC}$.

1.6 Proof of proposition 5

Since ${\pi }_{m}^{OF*}-{\pi }_{m}^{OC*}=(2bs+{b}^{2}r+(2-r)c)(c-{b}^{2})r/8{c}^{2}$, if $c-{b}^{2}>0$, we have ${\pi }_{m}^{OF*}>{\pi }_{m}^{OC*}$; otherwise, ${\pi }_{m}^{OF*}<{\pi }_{m}^{OC*}$.

Since ${\pi }_{m}^{OF*}-{\pi }_{m}^{CF*}=(2bs+{b}^{2}r\beta +(2-r\beta )c)(c-{b}^{2})r\beta /8{c}^{2}$, if $c-{b}^{2}>0$, we have ${\pi }_{m}^{OF*}>{\pi }_{m}^{CF*}$; otherwise, ${\pi }_{m}^{OF*}<{\pi }_{m}^{CF*}$.

Let ${\pi }_{m}^{CF*}-{\pi }_{m}^{OC*}=(c-{b}^{2})r(1-\beta )(2bs+{b}^{2}r(\beta +1)+(2-r(\beta +1))c)/8{c}^{2}$; if $c-{b}^{2}>0$, we derive that ${\pi }_{m}^{CF*}>{\pi }_{m}^{OC*}$; otherwise, ${\pi }_{m}^{CF*}<{\pi }_{m}^{OC*}$.

Therefore, if $c-{b}^{2}>0$, we have ${\pi }_{m}^{OF*}>{\pi }_{m}^{CF*}>{\pi }_{m}^{OC*}$; otherwise, ${\pi }_{m}^{OF*}<{\pi }_{m}^{CF*}<{\pi }_{m}^{OC*}$.