Strategic introduction for competitive fresh produce in an e-commerce platform with demand information sharing

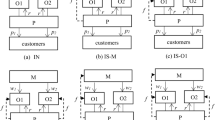
Abstract

To satisfy consumers’ diverse demands for fresh produce, the supplier may introduce competitive fresh produce through the reselling or agency channel of the platform to expand market coverage. Under the uncertain market environment, the supplier faces the problem of how to choose the appropriate product introduction strategy to promote information sharing cooperation, and the platform faces how to implement information sharing strategy under different product introduction strategies. This paper attempts to solve these problems and provide practical guidance for the cooperation between the supplier and the platform. Aiming at a fresh produce supply chain comprised of a supplier providing the freshness-keeping effort and a platform owning private demand information, we model a multistage game under asymmetric information to study the two strategies. Our results indicate that the platform may share information voluntarily, depending on the competition intensity and freshness sensitivity. To promote the information sharing cooperation with the platform, the supplier may choose introduction with agency selling even if a high commission fee is charged. Since information sharing promotes the product introduction strategy and vice versa, we reveal a complementary relationship between the two strategies. Interestingly, we find that introducing competitive fresh produce may increase the demand for original fresh produce when the freshness sensitivity is high. However, the platform may suffer from introduction with agency selling even at a high commission rate in some cases.

Appendix

Assumption 1

$0 < \eta < \overline{\eta }$, where $\overline{\eta } = \min (\sqrt {\frac{4b + 4}{{(1 - 2\alpha )b + 3 - 2\alpha }}} ,\sqrt {2 + 2b} )$.

In practice, the higher freshness sensitivity means consumers care much about the freshness of fresh produce purchased online. However, product freshness cannot continuously affect consumer demand, denoting an upper limit on the freshness sensitivity. Additionally, this assumption ensures that all the equilibriums and profits are positive.

Proof of Theorem 1

According to backward induction, the sales price of original fresh produce is solved first. We can know that the expected profit of the platform is concave with $p_{1}$ due to it satisfies $\frac{{\partial^{2} E\pi_{o} }}{{\partial p_{1}^{2} }} = - 2$. Let $\frac{{\partial E\pi_{o} }}{{\partial p_{1} }} = 0$, so we can derive $p_{1}^{U * } (w_{1} ,\tau ) = \frac{{E(a|Y) + w_{1} - \eta (1 - \tau )}}{2}$. If the platform shares information (does not share)with the supplier, the supplier can use $p_{1}^{U * } (w,\tau ) = \frac{{E(a|Y) + w_{1} - \eta (1 - \tau )}}{2}$ ($p_{1}^{U * } (w_{1} ,\tau ) = \frac{{\overline{a} + w_{1} - \eta (1 - \tau )}}{2}$) to decide the wholesale price $w_{1}$ and freshness-keeping effort $\tau$.

Next, we first verify that the expected profit of the supplier is concave with $w_{1}$ and $\tau$. The Hessian matrix of $E\pi_{s}^{U}$ is

$$H\left( {w_{1} ,\tau } \right) = \left( \begin{gathered} \frac{{\partial^{2} E\pi_{s} }}{{\partial w_{1}^{2} }} \, \frac{{\partial^{2} E\pi_{s} }}{{\partial w_{1} \partial \tau }} \, \hfill \\ \frac{{\partial^{2} E\pi_{s} }}{{\partial \tau \partial w_{1} }} \, \frac{{\partial^{2} E\pi_{s} }}{{\partial \tau^{2} }} \hfill \\ \end{gathered} \right) = \left( {\begin{array}{*{20}c} { - 1} & {\frac{\eta }{2}} \\ {\frac{\eta }{2}} & { - 1} \\ \end{array} } \right)$$

where $H_{1} = - 1 < 0$, $H_{2} = 1 - \eta^{2} /4$. To ensure the Hessian matrix is negative, it should satisfy that $H_{2} > 0$, namely, $\eta < 2$. Under this condition, let $\frac{{\partial E\pi_{s} }}{\partial \tau } = 0$ and $\frac{{\partial E\pi_{s} }}{{\partial w_{1} }} = 0$, we can derive the equilibrium wholesale price $w_{1}^{U * }$ and freshness-keeping effort $\tau^{U * }$. Take the expression of $w_{1}^{U * }$ and $\tau^{U * }$ into the function $p_{1}^{U * } (w_{1} ,\tau ) = \frac{{E(a|Y) + w_{1} - \eta (1 - \tau )}}{2}$, we can derive the equilibrium sales price $p_{1}^{U * }$.

Finally, take the expressions of $w_{1}^{U * }$, $\tau^{U * }$ and $p_{1}^{U * }$ into the expected profit functions of the supplier and the platform under no introduction, we can derive the expected profits of the supplier and the platform, as shown in the following.

$E\pi_{s}^{UI * } = \frac{{(\hat{H} - \eta )^{2} + (\hat{L} - \eta )^{2} }}{{16 - 4{\mkern 1mu} \eta^{2} }}$, $E\pi_{s}^{UN * } = \frac{{(\overline{a} - \eta )^{2} }}{{8 - 2\eta^{2} }}$,

$E\pi_{o}^{UI * } = \frac{{(\hat{H} - \eta )^{2} + (\hat{L} - \eta )^{2} }}{{2(4 - \eta^{2} )^{2} }}$, $E\pi_{o}^{UN * } = \frac{{(4\hat{H} - 2\overline{a} - 2\eta - \eta^{2} (\hat{H} - \overline{a}))^{2} }}{{8(4 - \eta^{2} )^{2} }} + \frac{{(4\hat{L} - 2\overline{a} - 2\eta - \eta^{2} (\hat{L} - \overline{a}))^{2} }}{{8(4 - \eta^{2} )^{2} }}$.

Proof of Proposition 1

From Theorem 1, we can derive that: $E\pi_{o}^{UI * } - E\pi_{o}^{UN * } = \frac{{(6 - \eta^{2} )(\eta^{2} - 2)(2\rho - 1)^{2} (H - L)^{2} }}{{16(4 - \eta^{2} )^{2} }}$. Thus we can derive that $sign(E\pi_{o}^{UI * } - E\pi_{o}^{UN * } ) = sign(\eta^{2} - 2)$. If $\eta < \sqrt 2$, $\eta^{2} - 2 < 0$, we have $E\pi_{o}^{UI * } - E\pi_{o}^{UN * } < 0$; if $\eta > \sqrt 2$, $\eta^{2} - 2 > 0$, we have $E\pi_{o}^{UI * } - E\pi_{o}^{UN * } > 0$.

Proof of Proposition 2

This proof is similar to that of Theorem 1.

We can derive the expected profits of the supplier and the platform, as shown in the follows.

$E\pi_{s}^{AI * } = \frac{{((1 - 2\alpha )b + 3 - 2\alpha )((\hat{H} - \eta )^{2} + (\hat{L} - \eta )^{2} )}}{{4(4b + 4 - ((1 - 2\alpha )b + 3 - 2\alpha )\eta^{2} )}} - C$, $E\pi_{s}^{AN * } = \frac{{((1 - 2\alpha )b + 3 - 2\alpha )(\overline{a} - \eta )^{2} }}{{2(4b + 4 - ((1 - 2\alpha )b + 3 - 2\alpha )\eta^{2} )}} - C$.

$E\pi_{o}^{AI * } = \frac{{(b + 1)((4\alpha - 1)b + 4\alpha + 1)((\hat{H} - \eta )^{2} + (\hat{L} - \eta )^{2} )}}{{(4b + 4 - M_{1} \eta^{2} )^{2} }}$,

$E\pi_{o}^{AN * } = \frac{{((1 - 2\alpha )b + 3 - 2\alpha )^{2} (1 - b)(\hat{H} - \hat{L})^{2} \eta^{4} - 8M_{3} (1 + b)\eta^{2} - 32\overline{a}\eta ((4\alpha - 1)b + 4\alpha + 1)(1 + b)^{2} - 4M_{4} (1 + b)^{2} }}{{16(1 + b)(4b + 4 - ((1 - 2\alpha )b + 3 - 2\alpha )\eta^{2} )^{2} }}$,where $M_{3} = ((2\alpha - 1)b^{2} - 2b - 2\alpha + 3)(\hat{H} - \hat{L})^{2} - 8\alpha b^{2} - 8\alpha b - 8\alpha - 2$ and $M_{4} = ((4\alpha - 5)(\hat{H}^{2} + \hat{L}^{2} ) + (8\alpha + 6)\hat{H}\hat{L})b + (4\alpha + 5)(\hat{H}^{2} + \hat{L}^{2} ) + (8\alpha - 6)\hat{H}\hat{L}$.

Proof of Proposition 2

This proof is similar to that of Proposition 1.

Proof of Theorem 3

This proof is similar to that of Theorem 1.

We can obtain the expected profits of the supplier and the platform, as shown in the following.

$E\pi_{s}^{RI * } = \frac{{((\hat{H} - \eta )^{2} + (\hat{L} - \eta )^{2} )}}{{4(2b + 2 - \eta^{2} )}} - C$, $E\pi_{s}^{RN * } = \frac{{(\overline{a} - \eta )^{2} }}{{2(2b + 2 - \eta^{2} )}} - C$

$$E\pi_{o}^{RI * } = \frac{{(1 - b^{2} )((\hat{H} - \eta )^{2} + (\hat{L} - \eta )^{2} )}}{{4(1 - b)(2b + 2 - \eta^{2} )^{2} }}$$

$$E\pi_{o}^{RN * } = \frac{{(\hat{H} - \hat{L})^{2} \eta^{4} - 4(((\hat{H} - \hat{L})^{2} - 1) - b)(1 + b)\eta^{2} - 8\overline{a}(1 + b)^{2} \eta + (1 + b)^{2} (5\hat{H}^{2} + 5\hat{L}^{2} - 6\hat{H}\hat{L})}}{{8(1 + b)(2b + 2 - \eta^{2} )^{2} }}$$

Proof of Proposition 3

This proof is similar to that of Proposition 1.

Proof of Proposition 4

According to Corollary 3, we know that there are four regions where the information sharing strategy of the platform are differentiated. Thus, we can discuss the supplier’s preference for the introduction strategy combined with these four regions, which are shown as follows.

• (1) When $\alpha < 3/4$, $b < b_{1}$ and $\eta < \eta_{1}$.

The platform will not share information under all three introduction strategies. Thus, we can get the supplier’s preference by comparing his profits under AN, RN and UN strategies.

First, we can find that $E\pi_{s}^{AN * } - E\pi_{s}^{RN * } = \frac{{(\overline{a} - \eta )^{2} (1/2 - \alpha )(1 + b)^{2} }}{{(2 + 2b - \eta^{2} )(4b + 4 - ((1 - 2\alpha )b + 3 - 2\alpha )\eta^{2} )}}$. Thus, we can derive that $sign(E\pi_{s}^{AN * } - E\pi_{s}^{RN * } ) = sign(1/2 - \alpha )$. If $\alpha < 1/2$, we have $E\pi_{s}^{AN * } > E\pi_{s}^{RN * }$; if $\alpha > 1/2$, we have $E\pi_{s}^{AN * } < E\pi_{s}^{RN * }$.

Next, we compare the value of $E\pi_{s}^{AN * } - E\pi_{s}^{UN * }$ if $\alpha < 1/2$, and the value of $E\pi_{s}^{RN * } - E\pi_{s}^{UN * }$ if $\alpha > 1/2$. By comparing $E\pi_{s}^{AN * }$ and $E\pi_{s}^{UN * }$, we can find that $E\pi_{s}^{AN * } - E\pi_{s}^{UN * } = \frac{f(C)}{{(\eta^{2} - 4)(4b + 4 - ((1 - 2\alpha )b + 3 - 2\alpha )\eta^{2} )}}$, where $f(C) = kC + m$, $k = (4b + 4 - ((1 - 2\alpha )b + 3 - 2\alpha )\eta^{2} )(4 - \eta^{2} )$, $m = 4(\alpha b + \alpha - 1)(\overline{a} - \eta )^{2}$. Thus, we can know that $sign(E\pi_{s}^{AN * } - E\pi_{s}^{UN * } ) = sign( - f(C))$. It is easy to verify that $k > 0$ and $m < 0$ when $\alpha < 1/2$. Thus, we can know that there exists $C_{1} = {\mkern 1mu} \frac{{{\mkern 1mu} 4(1 - \alpha - \alpha {\mkern 1mu} b){\mkern 1mu} (\overline{a} - \eta )^{2} }}{{(4 - \eta^{2} )(4{\mkern 1mu} b + 4 - M_{1} \eta^{2} )}}$, when $C < C_{1}$, $f(C) < 0$, and $E\pi_{s}^{AN * } > E\pi_{s}^{UN * }$; when $C > C_{1}$, $f(C) > 0$, and $E\pi_{s}^{AN * } < E\pi_{s}^{UN * }$. Furthermore, we can derive that $E\pi_{s}^{RN * } - E\pi_{s}^{UN * } = \frac{f(C)}{{(\eta^{2} - 4)(2 + 2b - \eta^{2} )}}$, where $f(C) = kC + m$, $k = (2b + 2 - \eta^{2} )(4 - \eta^{2} )$, $m = (b - 1)(\overline{a} - \eta )^{2}$. Thus, we can know that $sign(E\pi_{s}^{RN * } - E\pi_{s}^{UN * } ) = sign( - f(C))$. It is easy to verify that $k > 0$ and $m < 0$. Thus, we can know that there exists $C_{4} = {\mkern 1mu} \frac{{(1 - b)({\mkern 1mu} {\mkern 1mu} \overline{a} - {\mkern 1mu} \eta )^{2} }}{{(4 - \eta^{2} )(2b + 2 - {\mkern 1mu} \eta^{2} )}}$, when $C < C_{4}$, $f(C) < 0$, and $E\pi_{s}^{RN * } > E\pi_{s}^{UN * }$; when $C > C_{4}$, $f(C) > 0$, and $E\pi_{s}^{RN * } < E\pi_{s}^{UN * }$.

• (2) When $\max (0,\eta_{1} ) < \eta < \eta_{2}$.

The platform will share information under the strategy of introduction with agency selling, and not share information under the other two introduction strategies. Thus, we can get the supplier’s preference by comparing his profits under AI, RN and UN strategies. The detailed proof process is similar to that of Part (1).

First, we compare $E\pi_{s}^{AI * }$ and $E\pi_{s}^{RN * }$, we can derive that there exists $\rho_{3} { = }\frac{1}{2}{ + }\sqrt {\frac{{(2\alpha - 1)(2(1 + b)(H + L) - 4(1 + b)\eta )^{2} }}{{2(H - L)^{2} (2b + 2 - \eta^{2} )(3 + b - 2b\alpha - 2\alpha )}}} > 1/2$, if $\rho < \min (\rho_{3} ,1)$, $E\pi_{s}^{AI * } < E\pi_{s}^{RN * }$; if $\rho > \rho_{3}$, $E\pi_{s}^{AI * } > E\pi_{s}^{RN * }$.

Next, we compare $E\pi_{s}^{AI * }$ and $E\pi_{s}^{UN * }$, we can know that there exists $C_{2} = {\mkern 1mu} \frac{\begin{gathered} {\mkern 1mu} [4(4\alpha + 4\alpha b - b - 5)\hat{H}^{2} + 4\hat{L}^{2} (4\alpha + 4\alpha b - b - 5) - 64\overline{a}\eta (\alpha b + \alpha - 1) \hfill \\ + 8\hat{H}\hat{L}(1 + b) - 2(((\hat{H} - \hat{L})^{2} - 16)(1 + b)\alpha + 32 - {\mkern 1mu} (b + 3)(\hat{H} - \hat{L})^{2} )\eta^{2} ] \hfill \\ \end{gathered} }{{8(\eta^{2} - 4)(4{\mkern 1mu} b + 4 - M_{1} \eta^{2} )}}$, when $C < C_{2}$, $E\pi_{s}^{AI * } > E\pi_{s}^{UN * }$; when $C > C_{2}$, $E\pi_{s}^{AI * } < E\pi_{s}^{UN * }$. Furthermore, we compare $E\pi_{s}^{RN * }$ and $E\pi_{s}^{UN * }$, we can know that there exists $C_{4} = {\mkern 1mu} \frac{{(1 - b)({\mkern 1mu} {\mkern 1mu} \overline{a} - {\mkern 1mu} \eta )^{2} }}{{(4 - \eta^{2} )(2b + 2 - {\mkern 1mu} \eta^{2} )}}$, when $C < C_{4}$, $E\pi_{s}^{RN * } > E\pi_{s}^{UN * }$; when $C > C_{4}$, $E\pi_{s}^{RN * } < E\pi_{s}^{UN * }$.

• (3) When $\eta_{2} < \eta < \sqrt 2$, we have that:

The platform will share information under the strategies of introduction with agency selling and reselling, and not share information under no introduction. Thus, we can derive the supplier’s preference by comparing his profits under AI, RI and UN strategies. The detailed proof process is also similar to that of Part (1).

First, we compare $E\pi_{s}^{AI * }$ and $E\pi_{s}^{RI * }$, we can get that: if $\alpha < 1/2$, we have $E\pi_{s}^{AI * } > E\pi_{s}^{RI * }$; if $\alpha > 1/2$, we have $E\pi_{s}^{AI * } < E\pi_{s}^{RI * }$. Next, we compare the value of $E\pi_{s}^{AI * } - E\pi_{s}^{UN * }$ if $\alpha < 1/2$, and the value of $E\pi_{s}^{RI * } - E\pi_{s}^{UN * }$ if $\alpha > 1/2$. By comparing $E\pi_{s}^{UN * }$ and $E\pi_{s}^{RI * }$, we can derive that there exisits $C_{5} = \frac{{{\mkern 1mu} 6\hat{H}^{2} - 4{\mkern 1mu} \hat{H}\hat{L} + 6{\mkern 1mu} \hat{L}^{2} - ((\hat{H} - \hat{L})^{2} + 8{\mkern 1mu} b - 8)\eta^{2} - 16{\mkern 1mu} (1 - b)\overline{a}\eta - 8\overline{a}^{2} b}}{{8(4 - \eta^{2} )(2b + 2 - {\mkern 1mu} \eta^{2} )}}$, when $C < C_{5}$, $E\pi_{s}^{RI * } > E\pi_{s}^{UN * }$; when $C > C_{5}$, $E\pi_{s}^{RI * } < E\pi_{s}^{UN * }$.

• (4) When $\eta > \sqrt 2$, we have that:

The platform will share information under all three introduction strategies. Thus, we can get the supplier’s preference by comparing his profits under AI, RI and UI strategies. The detailed proof process is also similar to that of Part (1).

First, we compare the value of $E\pi_{s}^{AI * } - E\pi_{s}^{UI * }$ if $\alpha < 1/2$, and the value of $E\pi_{s}^{RI * } - E\pi_{s}^{UI * }$ if $\alpha > 1/2$. By comparing $E\pi_{s}^{AI * }$ and $E\pi_{s}^{UI * }$, we can know that there exists $C_{3} = {\mkern 1mu} \frac{{{\mkern 1mu} 2(\alpha {\mkern 1mu} b + \alpha - 1){\mkern 1mu} ((\hat{H} - \eta )^{2} + (\hat{L} - \eta )^{2} )}}{{(\eta^{2} - 4)(4{\mkern 1mu} b + 4 - M_{1} \eta^{2} )}}$, when $C < C_{3}$, $E\pi_{s}^{AI * } > E\pi_{s}^{UI * }$; when $C > C_{3}$, $E\pi_{s}^{AI * } < E\pi_{s}^{UI * }$. Furthermore, we compare the value of $E\pi_{s}^{RI * } - E\pi_{s}^{UN * }$. We can know that there exists $C_{6} = {\mkern 1mu} \frac{{{\mkern 1mu} (1 - b)((\hat{H} - \eta )^{2} + (\hat{L} - \eta )^{2} )}}{{2(4 - \eta^{2} )(2b + 2 - {\mkern 1mu} \eta^{2} )}}$, when $C < C_{6}$, $E\pi_{s}^{RI * } > E\pi_{s}^{UN * }$; when $C > C_{6}$, $E\pi_{s}^{RI * } < E\pi_{s}^{UN * }$.

Based on the above analysis, we can derive Proposition 4.

where $\rho_{3} { = }\frac{1}{2}{ + }\sqrt {\frac{{(2\alpha - 1)(2(1 + b)(H + L) - 4(1 + b)\eta )^{2} }}{{2(H - L)^{2} (2b + 2 - \eta^{2} )(3 + b - 2b\alpha - 2\alpha )}}}$, $C_{j1} = \left\{ {\begin{array}{*{20}c} {C_{1} } & {\eta < \eta_{1} } \\ {C_{2} } & {\eta_{1} < \eta < \sqrt 2 } \\ {C_{3} } & {\sqrt 2 < \eta < \overline{\eta }} \\ \end{array} } \right.$, and $C_{j2} = \left\{ {\begin{array}{*{20}c} {C_{4} } & {\eta < \eta_{2} } \\ {C_{5} } & {\eta_{2} < \eta < \sqrt 2 } \\ {C_{6} } & {\sqrt 2 < \eta < \overline{\eta }} \\ \end{array} } \right.$,

Proof of Proposition 5

• (1) The impact of the strategy of introduction with agency selling on the platform.

  • (i) When $\alpha < 3/4$, $b < b_{1}$, and $\eta < \eta_{1}$, we compare the platform’s profit under the AN and UN strategies.

    $E\pi_{o}^{AN * } - E\pi_{o}^{UN * } = \frac{{f(\rho )_{1} }}{{8(1 + b)(4 - \eta^{2} )^{2} (4b + 4 - ((1 - 2\alpha )b + 3 - 2\alpha )\eta^{2} )^{2} }}$, where $f(\rho )_{1} = A_{1} \rho^{2} + B_{1} \rho + E_{1}$ is a quadratic equation of $\rho$, $A_{1} = - 4b(H - L)^{2} (4 - \eta^{2} )^{2} (4b + 4 - ((1 - 2\alpha )b + 3 - 2\alpha )\eta^{2} )^{2} < 0$, $B_{1} = - A_{1} > 0$, and $\Delta = B_{1}^{2} - 4A_{1} E_{1} = 16(1 + b)A_{1} f(\eta )_{1} (H + L - 2\eta )^{2}$, and $f(\eta )_{1} = ((2{\mkern 1mu} \alpha^{2} - 4{\mkern 1mu} \alpha + 1)b^{2} + (4{\mkern 1mu} \alpha^{2} - 12{\mkern 1mu} \alpha + 3)b + 2{\mkern 1mu} \alpha^{2} - 8{\mkern 1mu} \alpha + 4)\eta^{4} + 8(1 + b)^{2} \left( {3\alpha - 1} \right)\eta^{2} - 16(1 + b){\mkern 1mu} (2\alpha b - b + 2\alpha )$. It is easy to verify that $sign(E\pi_{o}^{AN * } - E\pi_{o}^{UN * } ) = sign(f(\rho )_{1} )$. Let the unique solution of $f(\rho )_{1} = 0$ equals $\rho_{4} = \frac{1}{2} + \sqrt {\frac{{4(1 + b)(H + L - 2\eta )^{2} f(\eta )_{1} }}{{b(4 - \eta^{2} )^{2} (H - L)^{2} (4b + 4 - ((1 - 2\alpha )b + 3 - 2\alpha )\eta^{2} )^{2} }}}$, we have that: if $\rho < \min (\rho_{4} ,1) = \overline{\rho }_{4}$, $f(\rho )_{1} > 0$, $E\pi_{o}^{AN * } > E\pi_{o}^{UN * }$; if $\rho > \rho_{4}$, $E\pi_{o}^{AN * } < E\pi_{o}^{UN * }$.

  • (ii) When $\max (0,\eta_{1} ) < \eta < \sqrt 2$, we compare the platform’s profit under the AI and UN strategies.

    $E\pi_{o}^{AI * } - E\pi_{o}^{UN * } = \frac{{f(\rho )_{2} }}{{16(4 - \eta^{2} )^{2} (4b + 4 - ((1 - 2\alpha )b + 3 - 2\alpha )\eta^{2} )^{2} }}$, where $f(\rho )_{2} = A_{2} \rho^{2} + B_{2} \rho + E_{2}$ is a quadratic equation of $\rho$, $A_{2} = - 4(H - L)^{2} (4 - \eta^{2} )^{2} f(\eta )_{2}$, $B_{2} = - A_{2}$, and $\Delta_{2} = B_{2}^{2} - 4A_{2} E_{2} = 32A_{2} f(\eta )_{1} (H + L - 2\eta )^{2}$, and $f(\eta )_{2} = ((2\alpha - 1)b + 2\alpha - 3)^{2} \eta^{4} + 4(2(2\alpha - 1)b^{2} + 8(\alpha - 1)b + 4{\mkern 1mu} \alpha - 6)\eta^{2} + 4(5 - 4{\mkern 1mu} \alpha )b^{2} + 32(1 - \alpha )b - 16\alpha + 12$. It is easy to verify that $sign(E\pi_{o}^{AI * } - E\pi_{o}^{UN * } ) = sign(f(\rho )_{2} )$. Let the unique solution of $f(\rho )_{2} = 0$ equals $\rho_{5} = \frac{1}{2} + \sqrt {\frac{{8(H + L - 2\eta )^{2} f(\eta )_{1} }}{{(4 - \eta^{2} )^{2} (H - L)^{2} f(\eta )_{2} }}}$, we have that: if $\rho < \min (\rho_{5} ,1) = \overline{\rho }_{5}$, $f(\rho )_{2} > 0$, $E\pi_{o}^{AI * } > E\pi_{o}^{UN * }$; if $\rho > \rho_{5}$, $E\pi_{o}^{AI * } < E\pi_{o}^{UN * }$.

  • (iii) When $\eta > \sqrt 2$, we compare the platform’s profit under the AI and UI strategies.

    $E\pi_{o}^{AI * } - E\pi_{o}^{UI * } = \frac{{ - f(\eta )_{1} ((\hat{H} - \eta )^{2} + (\hat{L} - \eta )^{2} )}}{{(4 - \eta^{2} )^{2} (4b + 4 - ((1 - 2\alpha )b + 3 - 2\alpha )\eta^{2} )^{2} }}$. It is easy to verify that $sign(E\pi_{o}^{AI * } - E\pi_{o}^{UI * } ) = sign( - f(\eta )_{1} )$. Let the unique solution of $f(\eta )_{1} = 0$ equal $\eta_{5}$ when $\eta > \sqrt 2$, we can derive that: if $\alpha > 1/2$ and $b > b_{5}$, it satisfies that $\eta_{5} < \overline{\eta }$. Therefore, we can find that when $\sqrt 2 < \eta < \min (\eta_{5} ,\overline{\eta })$, it satisfies $E\pi_{o}^{AI * } > E\pi_{o}^{UI * }$; when $\alpha > 1/2$, $b > b_{5}$, and $\eta_{5} < \eta < \overline{\eta }$, it satisfies $E\pi_{o}^{AI * } < E\pi_{o}^{UI * }$, where $b_{5}$ is the unique solution of the equation $f(b) = (2\alpha^{2} - 4{\mkern 1mu} \alpha + 1)b^{3} + 2(3{\mkern 1mu} \alpha^{2} - 2{\mkern 1mu} \alpha )b^{2} + (6\alpha^{2} - 4{\mkern 1mu} \alpha + 3)b + 2\alpha^{2} - 4\alpha = 0$ and $\eta_{5} = \sqrt {\frac{{4{\mkern 1mu} b^{2} - 12{\mkern 1mu} (1 + b)^{2} \alpha + 8{\mkern 1mu} b + 4 + 4{\mkern 1mu} \sqrt {(\alpha {\mkern 1mu} b + \alpha - 1)^{2} (1 + b)(4{\mkern 1mu} \alpha {\mkern 1mu} b + 4{\mkern 1mu} \alpha - b + 1)} }}{{2{\mkern 1mu} (1 + b)^{2} \alpha^{2} - 4(b^{2} + 3{\mkern 1mu} b + 2)\alpha + b^{2} + 3{\mkern 1mu} b + 4}}}$.

Combining (i)(ii)(iii), we can derive Proposition 5(1).

where $\tilde{\rho } = \left\{ {\begin{array}{*{20}c} {\overline{\rho }_{4} } & {\alpha < 3/4,b < b_{1} ,\eta < \eta_{1} } \\ {\overline{\rho }_{5} } & {\max (\eta_{1} ,0) < \eta < \sqrt 2 } \\ \end{array} } \right.$, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{\rho } = \left\{ {\begin{array}{*{20}c} {\rho_{4} } & {\alpha < 3/4,b < b_{1} ,\eta < \eta_{1} } \\ {\rho_{5} } & {\max (\eta_{1} ,0) < \eta < \sqrt 2 } \\ \end{array} } \right.$.

• (2) The impact of the strategy of introduction with reselling on the platform.

When $\eta < \eta_{2}$, we compare the platform’s profit under the RN and UN strategies. When $\eta_{2} < \eta < \sqrt 2$, we compare the platform’s profit under the RI and UN strategies. When $\eta > \sqrt 2$, we compare the platform’s profit under the RI and UI strategies. It is easy to verify that $E\pi_{o}^{R * } > E\pi_{o}^{U * }$ in these regions, so we have omitted the detailed proof process.