Abstract
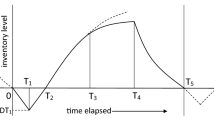
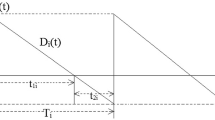
This paper investigates an economic order quantity (EOQ) problem with imperfect quality items, where the percentage of imperfect quality items in each lot is characterized as a random fuzzy variable while the setup cost per lot, the holding cost of each unit item per day, and the inspection cost of each unit item are characterized as fuzzy variables, respectively. In order to maximize the expected long-run average profit, a random fuzzy EOQ model is constructed. Since it is almost impossible to find an analytic method to solve the proposed model, a particle swarm optimization (PSO) algorithm based on the random fuzzy simulation is designed. Finally, the effectiveness of the designed algorithm is illustrated by a numerical example.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Chang H. (2004) An application of fuzzy sets theory to the EOQ model with imperfect quality items. Computers and Operations Research 31: 2079–2092
Cheng C. (1991). An economic order quantity model with demand-dependent unit production cost and imperfect production processes. IIE Transactions 23: 23–28
Eberhart R., Shi Y. (2001). Particle swarm optimization: Developments, applications and resources. IEEE International Conference on Evolutionary Computation 1: 81–86
Goyal S., Cárdenas-Barrón L. (2002). Note on: Economic production quantity model for items with imperfect quality a practical approach. International Journal of Production Economics 77: 85–87
Kennedy J., Eberhart R. (1995). Particle swarm optimization. IEEE International Conference on Neural Networks 4: 1942–1948
Kwakernaak H. (1978). Fuzzy random variables-I. Information Sciences 15: 1–29
Kwakernaak H. (1979). Fuzzy random variables-II. Information Sciences 17: 253–278
Li X., Liu B. (2006a) New independence definition of fuzzy random variable and random fuzzy variable. World Journal of Modelling and Simulation 2: 338–342
Li, X., & Liu, B. (2006b). Maximum variance theorems for various types of uncertain variable. Technical Report.
Liu B. (2002a) Theory and practice of uncertain programming. Physica-Verlag, Heidelberg
Liu B., Liu Y. (2002) Expected value of fuzzy variable and fuzzy expected value models. IEEE Transactions on Fuzzy Systems 10: 445–450
Liu B. (2002b). Toward fuzzy optimization without mathematical ambiguity. Fuzzy Optimization and Decision Making 1: 43–63
Liu B. (2002c) Random fuzzy dependent-chance programming and its hybrid intelligent algorithm. Information Sciences 141: 259–271
Liu Y., Liu B. (2003) Expected value operator of random fuzzy variable and random fuzzy expected value models. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 11: 195–215
Liu B. (2004) Uncertainty theory: An introduction to its axiomatic foundation. Springer-Verlag, Berlin
Liu B. (2006a) A survey of credibility theory. Fuzzy Optimization and Decision Making 5: 387–408
Liu Y. (2005) Fuzzy programming with recourse. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 13: 381–413
Liu Y. (2006b) Convergent results about the use of fuzzy simulation in fuzzy optimization problems. IEEE Transactions on Fuzzy Systems 14: 295–304
Park K. (1987) Fuzzy-set theoretic interpretation of economic order quantity. IEEE Transactions on Systems, Man, and Cybernet 17: 1082–1084
Petrović D., Petrović R., Vujošević M. (1996) Fuzzy models for the newsboy problem. International Journal of Production Economics 45: 435–441
Porteus E. (1986) Optimal lot sizing, process quality improvement and setup cost reduction. Operations Research 34: 137–144
Rosenblatt M., Lee H. (1986) Economic production cycles with imperfect production processes. IIE Transactions 18: 48–55
Ross S. (1996) Stochastic Processes. Wiley, New York
Salameh M., Jaber M. (2000) Economic production quantity model for items with imperfect quality. International Journal of Production Economics 64: 59–64
Schwaller R. (1988) EOQ under inspection costs. Production and Inventory Management 29: 22–24
Shi, Y., Eberhart, R. (1998). A modified particle swarm optimizer. IEEE International Conference on Evolutionary Computation 69–73.
Vujošević M., Petrović D., Petrović R. (1996) EOQ formula when inventory cost is fuzzy. International Journal of Production Economics 45: 499–504
Waters C. (1994). Inventory Control and Management. Wiley, Chichester
Zhang X., Gerchak Y. (1990) Joint lot sizing and inspection policy in an EOQ model with random yield. IIE Transactions 22: 41–47
Zhao R., Tang W., Yun H. (2006) Random fuzzy renewal process. European Journal of Operational Research 169: 189–201
Zhao, R., & Tang, W. (2006). Random fuzzy renewal reward process. Technical Report.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wang, X., Tang, W. & Zhao, R. Random fuzzy EOQ model with imperfect quality items. Fuzzy Optim Decis Making 6, 139–153 (2007). https://doi.org/10.1007/s10700-007-9002-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10700-007-9002-1