Abstract
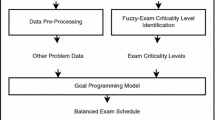
We consider examination courses scheduling at university. Two basic courses sharing at least one student cannot be scheduled at the same time. This scheduling problem will be stated as a graph coloring problem. The stability of the scheduled solution would be desirable in the sense that it remains valid also if some additional students want to do the exams, for example those who failed in earlier examination sessions. This stability is defined as the robustness of scheduling courses. We consider a mean value of the fuzzy number of courses incompatibilities as the robustness measure.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Chanas S., Nowakowski M. (1998). Single value simulation of fuzzy variable. Fuzzy Sets and Systems 25(1): 43–57
Gładysz B., Kuchta D. (2003a) Minimization of the expected number of late jobs in a single machine system with fuzzy processing times and fuzzy due dates. Operation Research and Decisions (in Polish) 4: 33–41
Gładysz, B., & Kuchta, D. (2003b). Minimization of the expected weighted number of jobs being late with fuzzy processing time in a one machine system. In M. Wagenknecht, & H. Rainer (Eds.), Proceedings of 3rd conference of the European society for fuzzy logic and technology. EUSFLAT 2003, Zittau, Germany, Zittau: EUSFLAT.
Kacprzyk J. (1986) Fuzzy sets in system analysis (in Polish). Warsaw: PWN
Yáñez J., Ramirez J. (2003) The robust coloring problem. European Journal of Operational Research 148: 546–558
Zadeh L.A. (1965) Fuzzy Sets. Information and Control 8: 338–353
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gładysz, B. Fuzzy robust courses scheduling problem. Fuzzy Optim Decis Making 6, 155–161 (2007). https://doi.org/10.1007/s10700-007-9003-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10700-007-9003-0