Abstract
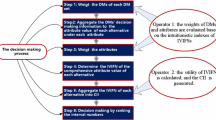
Intuitionistic fuzzy numbers, each of which is characterized by the degree of membership and the degree of non-membership of an element, are a very useful means to depict the decision information in the process of decision making. In this article, we investigate the group decision making problems in which all the information provided by the decision makers is expressed as intuitionistic fuzzy decision matrices where each of the elements is characterized by intuitionistic fuzzy number, and the information about attribute weights is partially known, which may be constructed by various forms. We first use the intuitionistic fuzzy hybrid geometric (IFHG) operator to aggregate all individual intuitionistic fuzzy decision matrices provided by the decision makers into the collective intuitionistic fuzzy decision matrix, then we utilize the score function to calculate the score of each attribute value and construct the score matrix of the collective intuitionistic fuzzy decision matrix. Based on the score matrix and the given attribute weight information, we establish some optimization models to determine the weights of attributes. Furthermore, we utilize the obtained attribute weights and the intuitionistic fuzzy weighted geometric (IFWG) operator to fuse the intuitionistic fuzzy information in the collective intuitionistic fuzzy decision matrix to get the overall intuitionistic fuzzy values of alternatives by which the ranking of all the given alternatives can be found. Finally, we give an illustrative example.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Atanassov K. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems 20, 87–96
Atanassov K. (1999). Intuitionistic fuzzy sets: Theory and applications. Heidelberg, Physica-Verlag
Atanassov K., Pasi G., Yager R.R. (2005). Intuitionistic fuzzy interpretations of multi-criteria multi-person and multi-measurement tool decision making. International Journal of Systems Science 36, 859–868
Bustince H., Burillo P. (1996). Vague sets are intuitionistic fuzzy sets. Fuzzy Sets and Systems 79, 403–405
Bustince H., Herrera F., Montero J. (2007). Fuzzy sets and their extensions: Representation, aggregation and models. Heidelberg, Physica-Verlag
Chan F.T.S., Kumar N. (2007). Global supplier development considering risk factors using fuzzy extended AHP-based approach. Omega 35, 417–431
Chen S.M., Tan J.M. (1994). Handling multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets and Systems 67, 163-172
Herrera F., Martínez L., Sánchez P.J. (2005). Managing non-homogeneous information in group decision making. European Journal of Operational Research 166, 115–132
Hong D.H., Choi C.H. (2000). Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets and Systems 114, 103–113
Horn R.A., Johnson C.R. (1990). Matrix analysis. Cambridge, Cambridge University Press
Kim S.H., Ahn B.S. (1999). Interactive group decision making procedure under incomplete information. European Journal of Operational Research 116, 498–507
Kim S.H., Choi S.H., Kim K. (1999). An interactive procedure for multiple attribute group decision making with incomplete information: Range-based approach. European Journal of Operational Research 118, 139–152
Szmidt E., Kacprzyk J. (2002). Using intuitionistic fuzzy sets in group decision making. Control and Cybernetics 31, 1037–1053
Szmidt E., Kacprzyk J. (2003). A consensus-reaching process under intuitionistic fuzzy preference relations. International Journal of Intelligent Systems 18, 837–852
Xu Z.S. (2005). An overview of methods for determining OWA weights. International Journal of Intelligent Systems 20, 843–865
Xu, Z. S. (2007). Intuitionistic preference relations and their application in group decision making. Information Sciences (in press).
Xu Z.S., Yager R.R. (2006). Some geometric aggregation operators based on intuitionistic fuzzy sets. International Journal of General Systems 35, 417–433
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Xu, Z. Multi-person multi-attribute decision making models under intuitionistic fuzzy environment. Fuzzy Optim Decis Making 6, 221–236 (2007). https://doi.org/10.1007/s10700-007-9009-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10700-007-9009-7