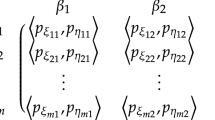Abstract
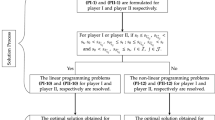
A generalized model for a two person zero sum matrix game with fuzzy goals and fuzzy payoffs via fuzzy relation approach is introduced, and it is shown to be equivalent to two semi-infinite optimization problems. Further, in certain special cases, it is observed that the two semi-infinite optimization problems reduce to (finite) linear programming problems which are dual to each other either in the fuzzy sense or in the crisp sense.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Bector C.R., Chandra S. (2000). On duality in linear programming under fuzzy environment. Fuzzy Sets and Systems 125: 317–325
Bector C.R., Chandra S. (2005). Fuzzy Mathematical Programming and Fuzzy Matrix Games. Berlin Heidelberg, Springer-Verlag
Bector C.R., Chandra S., Vijay V. (2004). Matrix games with fuzzy goals and fuzzy linear programming duality. Fuzzy Optimization and Decision Making 3: 263–277
Bellman R.E., Zadeh L.A. (1970). Decision making in a fuzzy environment. Management Science, 17: 141–164
Dubois D., Prade H. (1983). Ranking fuzzy numbers in the setting of possibility theory. Information Sciences 30: 183–224
Duffin, R. J., Jeroslow, R. G., & Karlovitz, L. A. (1983). Duality in semi-infinite linear programming, semi-infinite programming and applications. In Lecture Notes in Economics and Mathematical Systems (Vol. 215, pp. 50–62). Springer, Berlin.
Inuiguchi M., Ichihashi H., Kume Y. (1993). Modality constrained problems: A unified approach to fuzzy ma thematical programming problems in the setting of possibility theory. Information Sciences 67: 93–126
Inuiguchi M., Ramik J., Tanino T., Vlach M. (2003). Satisficing solutions and duality in interval and fuzzy linear programming. Fuzzy Sets and Systems 135: 151–177
Kaufmann A., Gupta M.M. (1991). Introduction to fuzzy arithmetic, theory and applications. New York, Van Nostrand Reinhold
Owen G. (1995). Game theory. San Diego, Academic Press
Ramik J. (2005). Duality in fuzzy linear programming: Some new concepts and results. Fuzzy Optimization and Decision Making 4: 25–39
Ramik J. (2006). Duality in fuzzy linear programming with possibility and necessity relations. Fuzzy Sets and Systems 157: 1283–1302
Rödder, W., Zimmermann, H.-J. (1980). Duality in Fuzzy Linear Programming. In: A. V. Fiacco, K. O. Kortanek (Eds.) In Extremal Methods and System Analysis, (pp. 415–429). Berlin-New York
Tijs S.H. (1969). Semi-infinite linear programs and semi-infinite matrix games. Nieuw Arch. Wisk 27: 197–214
Vijay V., Chandra S., Bector C.R. (2005). Matrix games with fuzzy goals and fuzzy payoffs. Omega: The International Journal of Management 33: 425–429
Wu H.-C. (2003). Duality theory in fuzzy linear programming problems with fuzzy coefficients. Fuzzy Optimization and Decision Making 2: 61–73
Zimmermann H.-J. (2001). Fuzzy set theory and its applications. Fourth edition. Nowell, Kluwer Academic Publishers
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Vijay, V., Mehra, A., Chandra, S. et al. Fuzzy matrix games via a fuzzy relation approach. Fuzzy Optim Decis Making 6, 299–314 (2007). https://doi.org/10.1007/s10700-007-9015-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10700-007-9015-9