Two storage inventory model in a mixed environment

Abstract

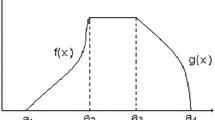
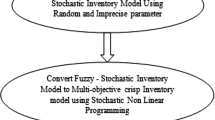
Multi-item inventory models with two storage facility and bulk release pattern are developed with linearly time dependent demand in a finite time horizon under crisp, stochastic and fuzzy-stochastic environments. Here different inventory parameters—holding costs, ordering costs, purchase costs, etc.—are assumed as probabilistic or fuzzy in nature. In particular cases stochastic and crisp models are derived. Models are formulated as profit maximization principle and three different approaches are proposed for solution. In the first approach, fuzzy extension principle is used to find membership function of the objective function and then it’s Graded Mean Integration Value (GMIV) for different optimistic levels are taken as equivalent stochastic objectives. Then the stochastic model is transformed to a constraint multi-objective programming problem using Stochastic Non-linear Programming (SNLP) technique. The multi-objective problems are transferred to single objective problems using Interactive Fuzzy Satisfising (IFS) technique. Finally, a Region Reducing Genetic Algorithm (RRGA) based on entropy has been developed and implemented to solve the single objective problems. In the second approach, the above GMIV (which is stochastic in nature) is optimized with some degree of probability and using SNLP technique model is transferred to an equivalent single objective crisp problem and solved using RRGA. In the third approach, objective function is optimized with some degree of possibility/necessity and following this approach model is transformed to an equivalent constrained stochastic programming problem. Then it is transformed to an equivalent single objective crisp problem using SNLP technique and solved via RRGA. The models are illustrated with some numerical examples and some sensitivity analyses have been presented.