Abstract
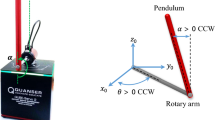
Fuzzy inference control uses fuzzy sets to describe the antecedents and consequents of If-Then rules. However, most surveys show the antecedents and consequents are uncertain sets rather than fuzzy sets. This fact provides a motivation to invent an uncertain inference control method. This paper gives an introduction to the design procedures of uncertain inference controller. As an example, an uncertain inference controller for balancing an inverted pendulum system is successfully designed. The computer simulation shows the developed uncertain inference controller is of good robustness.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Chen X. W., Liu B. (2010) Existence and uniqueness theorem for uncertain differential equations. Fuzzy Optimization and Decision Making 9(1): 69–81
Gao X., Gao Y., Ralescu D. A. (2010) On Liu’s inference rule for uncertain systems. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 18(1): 1–11
Guan J. W., Bell D. A. (1997) Approximate reasoning and evidence theory. Information Sciences 96: 207–235
Huang X. X. (2011) Mean-risk model for uncertain portfolio selection. Fuzzy Optimization and Decision Making 10(1): 71–89
Liu B. (2007) Uncertainty theory. (2nd ed.). Springer, Berlin
Liu B. (2010a) Uncertainty theory: A branch of mathematics for modeling human uncertainty. Springer, Berlin
Liu B. (2010b) Uncertain set theory and uncertain inference rule with application to uncertain control. Journal of Uncertain Systems 4(2): 83–98
Liu B. (2012) Why is there a need for uncertainty theory?. Journal of Uncertain Systems 6(1): 3–10
Liu, B. (2012). Membership functions and operational law of uncertain sets. Fuzzy Optimization and Decision Making.
Mamdani E. H. (1974) Applications of fuzzy algorithms for control of a simple dynamic plant. Proceedings of IEEE 121(12): 1585–1588
Pedrycz W. (1993) Fuzzy control and fuzzy systems. (2nd ed.). Wiley, New York
Peng Z. X., Iwamura K. (2010) A sufficient and necessary condition of uncertainty distribution. Journal of Interdisciplinary Mathematics 13(3): 277–285
Ray K. S., Majumder D. D. (1984) Application of circle criteria for stability analysis of linear SISO and MIMO syatem associated with fuzzy logic controllers. IEEE Transactions on Systems, Man and Cybernatics 14(2): 345–349
Tanaka K., Sano M. (1992) Stability analysis and design of fuzzy control systems. Fuzzy Sets and Systems 45: 135–156
Takagi T., Sugeno M. (1985) Fuzzy identification of system and its applications to modeling and control. IEEE Transactions on Systems, Man and Cybernatics 15(1): 116–132
Tasukamoto, Y. (1979). Fuzzy logic based on Lukasiewicz logic and its application to diagnosis and control, Ph.D. Dissertation, Tokyo Institute of Technology.
Turksen I. B., Zhong Z. (1988) An approximate analogical reasoning approach based on similarity measures. IEEE Transactions on Systems, Man and Cybernetics 18(6): 1049–1056
Wang G. J. (1999) On the logic foundation of fuzzy reasoning. Information Sciences 117: 47–88
Zadeh L. A. (1973) Outline of a new approach to the analysis of complex systems and decision processes. IEEE Transactions on Systems, Man, and Cybernetics 3(1): 28–44
Zhang Z. M. (2011) Some discussions on uncertain measure. Fuzzy Optimization and Decision Making 10(1): 31–43
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gao, Y. Uncertain inference control for balancing an inverted pendulum. Fuzzy Optim Decis Making 11, 481–492 (2012). https://doi.org/10.1007/s10700-012-9124-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10700-012-9124-y