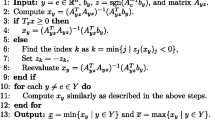Abstract
The future returns of each securities cannot be correctly reflected by the data in the past, therefore the expert’s judgements and experiences should be considered to estimate the security returns for the future. In this paper, we propose an interval portfolio selection model in which both the returns and the risks of assets are defined as intervals. By using interval and convex analysis, we solve this model and get the noninferior solution. Finally, an example is given to illustrate our results. The interval portfolio selection model improves and generalizes the Markowitz’s mean-variance model and the results of Deng et al. (Eur J Oper Res 166(1):278–292, 2005).
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Bertsimas, D., & Thiele, A. (2006). Robust and data-driven optimization: Modern decision making under uncertainty. In Tutorials in operations research (pp. 95–122). INFORMS.
Best, M. J., & Grauer, R. R. (1991). On the sensitivity of mean-variance-efficient portfolios to changes in asset means: some analytical and computational results. Review of Financial Studies, 4(2), 315–342.
Best, M. J., & Grauer, R. R. (1991). Sensitivity analysis for mean-variance portfolio problems. Management Science, 37(8), 980–989.
Deng, X. T., Li, Z. F., & Wang, S. Y. (2005). A minimax portfolio selection strategy with equilibrium. European Journal of Operational Research, 166(1), 278–292.
Elton, E. J., Gruber, M. J., & Urich, T. J. (1978). Are betas best? Journal of Finance, 33(5), 1375–1384.
Fan, K. (1953). Minimax theorems. Proceedings of the National Academy of Sciences of the United States of America, 39(1), 42–47.
Giove, S., Funari, S., & Nardelli, C. (2006). An interval portfolio selection problem based on regret function. European Journal of Operational Research, 170(1), 253–264.
Inuiguchi, M., & Ramík, J. (2000). Possibilistic linear programming: A brief review of fuzzy mathematical programming and a comparison with stochastic programming in portfolio selection problem. Fuzzy Sets and Systems, 111(1), 3–28.
Inuiguchi, M., & Sakawa, M. (1995). Minimax regret solution to linear programming problems with an interval objective function. European Journal of Operational Research, 86(3), 526–536.
Konno, H., & Yamazaki, H. (1991). Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market. Management Science, 37(5), 519–531.
Lai, K. K., Wang, S. Y., Xu, J. P., Zhu, S. S., & Fang, Y. (2002). A class of linear interval programming problems and its application to portfolio selection. IEEE Transactions on Fuzzy Systems, 10(6), 698–704.
Lin, C. C., & Liu, Y. T. (2008). Genetic algorithms for portfolio selection problems with minimum transaction lots. European Journal of Operational Research, 185(1), 393–404.
Mao, J. C. T. (1970). Models of capital budgeting, E-V VS E-S. Journal of Financial and Quantitative Analysis, 4(5), 657–675.
Markowitz, H. M. (1952). Portfolio selection. Journal of Finance, 7(1), 77–91.
Markowitz, H. M. (1987). Mean-variance analysis in portfolio choice and capital markets. Oxford: Basil Blackwell.
Markowitz, H. M. (1991). Portfolio selection: Efficient diversification of investments (2nd ed.). Oxford: Basil Blackwell.
Neumaier, A. (1990). Interval methods for systems of equations. Cambridge: Cambridge University Press.
Rohn, J. (1989). Systems of linear interval equations. Linear algebra and its applications, 126, 39–78.
Rohn, J. (1993). Inverse interval matrix. SIAM Journal on Numerical Analysis, 30(3), 864–870.
Sengupta, A., & Pal, T. K. (2000). On comparing interval numbers. European Journal of Operational Research, 127(1), 28–43.
Wang, S. Y., & Zhu, S. S. (2002). On fuzzy portfolio selection problems. Fuzzy Optimization and Decision Making, 1(4), 361–377.
Xia, Y. S., Liu, B. D., Wang, S. Y., & Lai, K. K. (2000). A model for portfolio selection with order of expected returns. Computers and Operations Research, 27(5), 409–422.
Yoshimoto, A. (1996). The mean-variance approach to portfolio optimization subject to transaction costs. Journal of the Operations Research Society of Japan, 39(1), 99–117.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (71101099, 70831005) and the Special Funds of Sichuan University of the Fundamental Research Funds for the Central Universities (SKQY201330).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wu, M., Kong, Dw., Xu, Jp. et al. On interval portfolio selection problem. Fuzzy Optim Decis Making 12, 289–304 (2013). https://doi.org/10.1007/s10700-013-9155-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10700-013-9155-z