Impacts of risk attitude and outside option on compensation contracts under different information structures

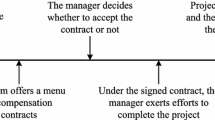
Abstract

We consider an agency problem where a firm (she) hires a manager (he) who has related managerial expertise to implement a new project. The manager’s managerial expertise is his private information and characterized as an uncertain variable. The revenue brought about by the project in the future is also assumed to be uncertain. In light of these challenges, this paper investigates the impacts of the manager’s risk attitude and the type-and-effort dependent outside option on the optimal compensation contracts under different information structures. Through developing the manager’s decision criterion based on his risk attitude instead of the expected-utility-maximization criterion, we find that, if the manager is conservative and the outside option’s revenue uncertainty is sufficiently high, the optimal commission rate will be distorted upwards under asymmetric managerial expertise information compared with that under symmetric managerial expertise information. Our analysis also confirms that the existence of a type-and-effort dependent outside option distorts up the compensation structure tailored at a fixed outside option. We further show that, comparing with the setting of a fixed outside option when the manager is aggressive, the presence of a type-and-effort dependent outside option results in a surprising phenomenon that the manager’s private information makes no distortion of the firm’s profit.

Appendix: Proofs

Proof of Proposition 1

Based on the expected value criterion, the firm’s expected profit

$$\begin{aligned} E[R_1-w(\theta ,R_1)]=(1-w_1(\theta ))(\theta +e_1)-w_0(\theta ). \end{aligned}$$

Based on the critical value criterion, if the manager accepts the contract, his $\alpha$-utility

$$\begin{aligned} \displaystyle \pi _1(\theta ,\theta )=w_0(\theta )+(\theta +e_1+(1-2\alpha )a_1)w_1(\theta )-\frac{1}{2}e_{1}^{2}. \end{aligned}$$

If the manager refuses the contract and opts for the outside option, his $\alpha$-utility

$$\begin{aligned} \displaystyle \pi _2(\theta )= & {} \theta +\frac{1}{2}+(1-2\alpha )a_2, \end{aligned}$$

where the manager always maximizes his profit by exerting an effort

$$\begin{aligned} \displaystyle e_{2}=\arg \max _{{\hat{e}}_2\geqslant 0} \pi _2(\theta ,\theta )=1. \end{aligned}$$

Because the firm’s expected profit is deceasing in the fixed payment $w_0$, at optimality, the individual rationality constraint should be binding, i.e., $\pi _1(\theta ,\theta )=\pi _2(\theta )$. Thus,

$$\begin{aligned} \displaystyle -w_0=(\theta +e_{1}+(1-2\alpha )a_1)w_1-\frac{1}{2}e_{1}^2-\theta -\frac{1}{2}-(1-2\alpha )a_2. \end{aligned}$$

Substituting the fixed payment into the firm’s objective function, we obtain

$$\begin{aligned} (1-2\alpha )(a_1w_1(\theta )-a_2)+e_{1}-\frac{1}{2}e_{1}^2-\frac{1}{2}, \end{aligned}$$

which is concave in $e_{1}$. Thus, we yield the manager’s optimal effort level $e_1^{SO}=1$ for the firm’s project by using the first-order condition $\partial \pi _F^{SO}/\partial e_{1}=0$. By substituting this optimal effort level into the firm’s simplified problem above, we simplify the firm’s problem to

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \max _{w_1(\theta )} \pi _F^{SO}=(1-2\alpha )(a_1w_1(\theta )-a_2)\\ \text{ subject } \text{ to: }\\ \displaystyle \quad 0\leqslant w_1(\theta )\leqslant 1.\\ \end{array} \right. \end{aligned}$$

Because the objective function is piecewise linear in $w_1(\theta )$, we focus on the corner point solutions $w_1(\theta )\in \{0,1\}$. To ensure the firm can get a positive and maximum profit, if $\alpha \leqslant \frac{1}{2}$ and $a_1>a_2$, the optimal incentive compensation rate is $w_1^{SO}(\theta )=1$; if $\alpha >\frac{1}{2}$ and $a_1,a_2>0$, the optimal incentive compensation rate is $w_1^{SO}(\theta )=0$. Following the determinate optimal incentive commission rate $w_1^{SO}$, the corresponding optimal fixed payment $w_0^{SO}$ for the manager can be derived immediately. The proof of the proposition is complete. $\square$

Proof of Proposition 2

If the manager accepts the contract, the manager will choose his own effort $e_1^{SU}$ to maximize his $\alpha$-profit

$$\begin{aligned} \displaystyle w_0(\theta )+[\theta +{\hat{e}}_1+(1-2\alpha )a_1]w_1(\theta )-\frac{1}{2}{\hat{e}_1}^{2}, \end{aligned}$$

which is concave in $\hat{e}_1$. The maximum is completely characterized by the first-order condition $e_1^{SU}=w_1(\theta )$. Furthermore, because the firm’s profit is deceasing in the fixed payment $w_0(\theta )$, at optimality, the incentive compatibility constraint should be binding, i.e., $\pi _1=\pi _2$. By substituting $e_1^{SU}$ and $e_{2}$ into the incentive compatibility constraint, we can rewrite the incentive compatibility constraint as

$$\begin{aligned} w_0+(\theta +(1-2\alpha )a_1)w_1+\frac{1}{2}w_{1}^2-\theta -\frac{1}{2}-(1-2\alpha )a_2=0.\\ \end{aligned}$$

After substituting the fixed payment $w_0$ and $e_1^{SU}$ into the objective function, the firm’s problem can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \max _{w_1(\theta )} \pi _F^{SU}=-\frac{1}{2}w_{1}^2+(1+(1-2\alpha )a_1)w_{1}-\frac{1}{2}-(1-2\alpha )a_2\\ \text{ subject } \text{ to: }\\ \displaystyle \quad 0\leqslant w_1(\theta )\leqslant 1.\\ \end{array} \right. \end{aligned}$$

There are two cases: (i) $\alpha \leqslant \frac{1}{2}$ and (ii) $\alpha >\frac{1}{2}$. To ensure the firm can get a positive and maximum profit, for case (i), we can obtain $w_1^{SU}=1$ and $a_1>a_2$. For case (ii), by the first-order condition, we can obtain $w_1^{SU}=1+(1-2\alpha )a_1$ and $a_{11}<a_{2}$ where $a_{11}=a_{1}-(\alpha -\frac{1}{2}a_{1}^{2})$.

Following the determinate optimal incentive commission rate $w_1^{SU}$, the optimal fixed payment $w_0^{SU}$ and the optimal effort level $e_{1}^{SU}$ for the manager can be obtained immediately. The proof of the proposition is complete. $\square$

Before giving the Proof of Proposition 3, we first simplify the expressions of both the incentive compatibility constraint for adverse selection and individual rationality constraint in Case AO. Define $\Psi (\theta ,\theta )=\pi _1(\theta ,\theta )-\pi _2(\theta )$.

Lemma 1

A compensation contract satisfies the incentive compatibility constraint for adverse selection and individual rationality constraint if and only if

• (i) $\displaystyle \frac{\mathrm {d} w_0(\theta )}{\mathrm {d}\theta }+(\theta +e+(1-2\alpha )a_1)\frac{\mathrm {d}w_1(\theta )}{\mathrm {d}\theta }=0,\quad \forall \theta \in [\underline{\theta },\overline{\theta }];$

• (ii) $\displaystyle \frac{\mathrm {d} w_1(\theta )}{\mathrm {d} \theta }\geqslant 0,\quad \forall \theta \in [\underline{\theta },\overline{\theta }];$

• (iii) $\displaystyle \Psi \left( \overline{\theta },\overline{\theta }\right) =0$.

Proof of Lemma 1

the incentive compatibility constraint for adverse selection can be written as

$$\begin{aligned} \pi _1(\theta ,\theta )\geqslant \pi _1(\theta ,{\hat{\theta }}), \quad \forall \theta , {\hat{\theta }} \in [\underline{\theta },\overline{\theta }], \end{aligned}$$

which means that $\pi _1(\theta ,{\hat{\theta }})$ obtains its maximal value at $\pi _1(\theta ,\theta )$, i.e., the manager can obtain his maximal profit $\pi _1(\theta ,{\hat{\theta }})$ if and only if $\hat{\theta }=\theta$. In other words, the manager with managerial expertise $\theta$ has no incentive to pretend to be a that with idea value ${\hat{\theta }}$. Thus, $\pi _1(\theta ,{\hat{\theta }})$ satisfies the first-order condition (i.e., local incentive compatibility constraint) $\frac{\partial \pi _1(\theta ,{\hat{\theta }})}{\partial {\hat{\theta }}}\bigm |_{{\hat{\theta }}=\theta }=0$ and the second-order condition $\frac{\partial ^{2} \pi _1(\theta ,{\hat{\theta }})}{\partial {\hat{\theta }}{2}}\bigm |_{{\hat{\theta }}=\theta }\leqslant 0$. The local incentive compatibility constraint

$$\begin{aligned} \frac{\mathrm {d} w_0(\theta )}{\mathrm {d} \theta }+(\theta +e_1+(1-2\alpha )a_1)\frac{\mathrm {d} w_1(\theta )}{\mathrm {d} \theta }=0,\quad \forall \theta \in [\underline{\theta },\overline{\theta }]. \end{aligned}$$

(1)

If we further differentiate the local incentive compatibility constraint with respect to $\theta$, we can obtain

$$\begin{aligned} \frac{\mathrm {d}^{2} w_0(\theta )}{\mathrm {d} \theta }+(\theta +e_1+(1-2\alpha )a_1)\frac{\mathrm {d}^{2} w_1(\theta )}{\mathrm {d} \theta ^{2}}+\frac{\mathrm {d} w_1(\theta )}{\mathrm {d} \theta }=0,\quad \forall \theta \in [\underline{\theta },\overline{\theta }]. \end{aligned}$$

(2)

By the second-order condition, we derive

$$\begin{aligned} \frac{\mathrm {d}^{2} w_0(\theta )}{\mathrm {d} \theta }+(\theta +e_1+(1-2\alpha )a_1)\frac{\mathrm {d}^{2} w_1(\theta )}{\mathrm {d} \theta ^{2}}\leqslant 0,\quad \forall \theta \in [\underline{\theta },\overline{\theta }]. \end{aligned}$$

(3)

On the basis of (2) and (3), we gain the monotonicity condition

$$\begin{aligned} \frac{\mathrm {d} w_1(\theta )}{\mathrm {d} \theta }\geqslant 0,\quad \forall \theta \in [\underline{\theta },\overline{\theta }]. \end{aligned}$$

(4)

Suppose, next, that both the local incentive compatibility and monotonicity conditions hold. Then it must be the case that all the manager’s incentive compatibility conditions hold. To see this result, without loss of generality, suppose that $\hat{\theta }>{\theta }$. by integrating the local incentive compatibility condition (1) and using the monotonicity condition (4), we can obtain

$$\begin{aligned} w_{0}(\theta )-w_{0}(\hat{\theta })= & {} -\int ^{\theta }_{\hat{\theta }}(x+e_1+(1-2\alpha )a_1)\frac{\mathrm {d}w_1(x)}{\mathrm {d} x}\mathrm {d} x \nonumber \nonumber \\\geqslant & {} (\theta +e_1+(1-2\alpha )a_1)w_1(\hat{\theta })-(\theta +e_1+(1-2\alpha )a_1)w_1(\theta ). \end{aligned}$$

Simplifying inequality above yields

$$\begin{aligned} w_{0}(\theta )+(\theta +e_1+(1-2\alpha )a_1)w_1(\theta ) \geqslant w_{0}(\hat{\theta })+(\theta +e_1+(1-2\alpha )a_1)w_1(\hat{\theta }). \end{aligned}$$

That is to say

$$\begin{aligned} \pi _1(\theta ,\theta )\geqslant \pi _1(\theta ,{\hat{\theta }}), \quad \forall \theta , {\hat{\theta }} \in [\underline{\theta },\overline{\theta }]. \end{aligned}$$

On the other hand, if $\hat{\theta }<{\theta }$, by integrating the local incentive compatibility condition (1) and using the monotonicity condition (4), we can also obtain

$$\begin{aligned} w_{0}(\theta )-w_{0}(\hat{\theta })= & {} -\int _{\hat{\theta }}^{\theta }(x+e_1+(1-2\alpha )a_1)\frac{\mathrm {d}w_1(x)}{\mathrm {d} x}\mathrm {d} x \\\geqslant & {} -(\theta +e_1+(1-2\alpha )a_1)w_1({\theta })+(\theta +e_1+(1-2\alpha )a_1)w_1(\hat{\theta }). \end{aligned}$$

Simplifying inequality above yields

$$\begin{aligned} w_{0}(\theta )+(\theta +e_1+(1-2\alpha )a_1)w_1(\theta ) \geqslant w_{0}(\hat{\theta })+(\theta +e_1+(1-2\alpha )a_1)w_1(\hat{\theta }). \end{aligned}$$

That is to say

$$\begin{aligned} \pi _1(\theta ,\theta )\geqslant \pi _1(\theta ,\hat{\theta }),\quad \forall \theta ,\hat{\theta }\in [\underline{\theta }, \overline{\theta }]. \end{aligned}$$

This result establishes the equivalence between the monotonicity condition together with the local incentive compatibility condition and the full set of the manager’s incentive constraints.

For part (iii),

$$\begin{aligned} \displaystyle \Psi (\theta ,\theta )= & {} \pi _1(\theta ,\theta )-\pi _2(\theta )\\&=w_0(\theta )+(\theta +e_1+(1-2\alpha )a_1)w_1(\theta )-\frac{1}{2}e_1^2-\theta -\frac{1}{2}-(1-2\alpha )a_2. \end{aligned}$$

Differentiating $\Psi$ with respect to $\theta$ yields

$$\begin{aligned} \displaystyle \frac{\mathrm {d} \Psi (\theta ,\theta )}{\mathrm {d} \theta }=\frac{\mathrm {d} w_0(\theta )}{\mathrm {d} \theta }+(\theta +e_1+(1-2\alpha )a_1)\frac{\mathrm {d} w_1(\theta )}{\mathrm {d} \theta }+w_1(\theta )-1=w_1(\theta )-1\leqslant 0. \end{aligned}$$

The individual rationality constraint is equivalent to

$$\begin{aligned} \Psi (\overline{\theta },\overline{\theta })\geqslant 0. \end{aligned}$$

The constraint is binding under the optimal mechanism because the firm will reap the redundant profit, so that $\Psi (\overline{\theta },\overline{\theta })=0$.$\square$

Proof of Proposition 3

Because

$$\begin{aligned} \Psi (\overline{\theta },\overline{\theta })=\pi _1(\overline{\theta },\overline{\theta })-\pi _2(\overline{\theta })=0 \end{aligned}$$

and

$$\begin{aligned} \frac{\mathrm {d}\pi _1(\theta ,\theta )}{\mathrm {d}\theta }=\frac{\mathrm {d} w_0(\theta )}{\mathrm {d} \theta }+(\theta +e_1+(1-2\alpha )a_1)\frac{\mathrm {d} w_1(\theta )}{\mathrm {d} \theta }+w_1(\theta )=w_1(\theta ), \end{aligned}$$

we can derive

$$\begin{aligned} \pi _1(\theta ,\theta )=\pi _1(\overline{\theta },\overline{\theta })-\int ^{\overline{\theta }}_{\theta }w_1(x)\mathrm {d}x=\overline{\theta }+(1-2\alpha )a_2+\frac{1}{2}-\int ^{\overline{\theta }}_{\theta }w_1(x)\mathrm {d}x. \end{aligned}$$

Combining the definition of $\pi _1(\theta ,\theta )$ yields

$$\begin{aligned} w_0(\theta )=\overline{\theta }+(1-2\alpha )a_2+\frac{1}{2}-\int ^{\overline{\theta }}_{\theta }w_1(x)\mathrm {d}x-(\theta +e_1+(1-2\alpha )a_1)w_1(\theta )+\frac{1}{2}e_1^2. \end{aligned}$$

By substituting the fixed wage into the objective function, we can derive

$$\begin{aligned} \pi _F^{AO}= & {} \int ^{\overline{\theta }}_{\underline{\theta }}\left[ \theta +e_1-\frac{1}{2}e_1^2+(1-2\alpha )a_1w_1(\theta )+\int ^{\overline{\theta }}_{\theta }w_1(x)\mathrm {d}x-\overline{\theta }\right. \\&\left. -(1-2\alpha )a_2-\frac{1}{2}\right] f(\theta )\mathrm {d}\theta . \end{aligned}$$

We can use the first-order condition $\partial \pi _F^{AO}/ \partial e_{1}=0$ to yields the first-best effort level. As a result, $e_{1}^{AO}=1$. Substitute it into the objective function and ignore the monotonicity constraint in Lemma 1. The firm’s problem can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \max _{w_1(\theta )} \pi _F^{AO}=\int ^{\overline{\theta }}_{\underline{\theta }}\left\{ \left[ (1-2\alpha )a_1+h(\theta )\right] w_1(\theta )+\theta -\overline{\theta }-(1-2\alpha )a_2\right\} f(\theta )\mathrm {d}\theta \\ \text{ subject } \text{ to: }\\ \displaystyle \quad 0\leqslant w_1(\theta )\leqslant 1,\quad \forall \theta \in [\underline{\theta },\overline{\theta }].\\ \end{array} \right. \end{aligned}$$

Because the objective function is piecewise linear in $w_1(\theta )$, we focus on the corner point solutions $w_1(\theta )\in \{0,1\}$. To ensure the firm can get a positive and maximum profit, if $\alpha \leqslant \frac{1}{2}$ and $a_1>a_2$, the optimal incentive compensation rate is $w_1^{SO}(\theta )=1$; if $\alpha >\frac{1}{2}$ and $a_{12}<a_2$, there are two cases: (i) $\underline{\theta }\leqslant \theta <\theta _1$ and (ii) $\theta _1\leqslant \theta \leqslant \overline{\theta }$. For case (i), we can obtain $w_1^{AO}(\theta )=0$. For case (ii), we can obtain $w_1^{AO}(\theta )=1$. Following the determinate optimal incentive commission rate $w_1^{SO}$, the corresponding optimal fixed payment $w_0^{SO}$ for the manager can be obtained immediately. The proof of the proposition is complete. $\square$

Before giving the Proof of Proposition 4, we first simplify the expressions of both the incentive compatibility constraint for adverse selection and individual rationality constraint in Case AU.

Lemma 2

A compensation contract satisfies the incentive compatibility constraint for adverse selection and individual rationality constraint if and only if

• (i) $\displaystyle \frac{\mathrm {d} w_0(\theta )}{\mathrm {d} \theta }+(\theta +(1-2\alpha )a_1)\frac{\mathrm {d} w_1(\theta )}{\mathrm {d} \theta }+w_1(\theta )\frac{\mathrm {d} w_1(\theta )}{\mathrm {d} \theta }=0,\quad \forall \theta \in [\underline{\theta },\overline{\theta }];$

• (ii) $\displaystyle \frac{\mathrm {d} w_1(\theta )}{\mathrm {d} \theta }\geqslant 0,\quad \forall \theta \in [\underline{\theta },\overline{\theta }];$

• (iii) $\displaystyle \Psi \left( \overline{\theta },\overline{\theta }\right) =0$.

Proof of Lemma 2

For parts (i) and (ii), if the manager’s true managerial expertise is $\theta$ but he selects the contract $(w_0({\hat{\theta }}),w_1({\hat{\theta }}))$, his $\alpha$-profit

$$\begin{aligned} \displaystyle \pi _1(\theta ,{\hat{\theta }})=w_0({\hat{\theta }})+(\theta +e+(1-2\alpha )a_1)w_1({\hat{\theta }})-\frac{1}{2}e_1^2. \end{aligned}$$

By the first-order condition, the manager maximizes his profit by exerting an effort

$$\begin{aligned} \displaystyle e_1=\arg \max _{{\hat{e}}_1\geqslant 0} \pi _1(\theta ,\hat{\theta })=w_1({\hat{\theta }}). \end{aligned}$$

His profit under this optimal effort

$$\begin{aligned} \displaystyle \pi _1(\theta ,{\hat{\theta }})=w_0(\hat{\theta })+(\theta +(1-2\alpha )a_1)w_1({\hat{\theta }})+\frac{1}{2}w_1(\hat{\theta })^2. \end{aligned}$$

Similarly, if the manager selects the contract $(w_0(\theta ),w_1(\theta ))$ based on his true managerial expertise $\theta$, his profit

$$\begin{aligned} \pi _1(\theta ,\theta )=w_0(\theta )+(\theta +(1-2\alpha )a_1)w_1(\theta )+\frac{1}{2}w_1(\theta )^2. \end{aligned}$$

The rest of the proof is similar to the Proof of Lemma 1. Therefore, the proof of the lemma is complete. $\square$

Proof of Proposition 4

Through the similar method used in the Proof of Proposition 3, the firm’s problem can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \max _{w_1(\theta )} \pi _F^{AU}=\int ^{\overline{\theta }}_{\underline{\theta }}\left\{ -\frac{1}{2}w_1(\theta )^2+\left[ 1+(1-2\alpha )a_1+h(\theta )\right] w_1(\theta )\right. \\ \quad \left. +(\theta -\overline{\theta }-(1-2\alpha )a_2)-\dfrac{1}{2}\right\} f(\theta )\mathrm {d}\theta \\ \text{ subject } \text{ to: }\\ \displaystyle \quad 0\leqslant w_1(\theta )\leqslant 1,\quad \forall \theta \in [\underline{\theta },\overline{\theta }].\\ \end{array} \right. \end{aligned}$$

(5)

The first-order variation and the second-order variation of the firm’s expected profit are derived as

$$\begin{aligned} \delta \pi _F^{AU}=\int ^{\overline{\theta }}_{\underline{\theta }}\left[ -w_1(\theta )+1+(1-2\alpha )a_1+h(\theta )\right] f(\theta )[\delta w_1(\theta )]\mathrm {d}\theta \end{aligned}$$

and

$$\begin{aligned} \delta ^{2}\pi _F^{AU}=-\int ^{\overline{\theta }}_{\underline{\theta }}f(\theta )[\delta w_1(\theta )]^{2}\mathrm {d}\theta . \end{aligned}$$

If $\alpha \leqslant \frac{1}{2}$, it exists a unique optimal solution $w_1^{AU}(\theta )=1$. To ensure the firm has a positive profit, $a_1$ and $a_2$ must satisfy $a_{1}>a_2$.

On the other hand, if $\alpha >\frac{1}{2}$, there are two cases: (i) $\underline{\theta }\leqslant \theta <\theta _1$ and (ii) $\theta _1\leqslant \theta \leqslant \overline{\theta }$. For case (i), we can obtain $w_1^{AU}(\theta )=1+(1-2\alpha )a_1+h(\theta )$. For case (ii), we can obtain $w_1^{AU}(\theta )=1$. To ensure the firm has a positive profit, $a_1$ and $a_2$ must satisfy $a_{13}<a_2$, where $a_{13}=a_1-\frac{1}{2(2\alpha -1)}\int ^{\theta _1}_{\underline{\theta }}[(1-2\alpha )a_1+h(\theta )]^2f(\theta )\mathrm {d}\theta$. Following the determinate optimal incentive commission rate $w_1^{AU}$, the corresponding optimal fixed payment $w_0^{AU}$ and the optimal effort level $e^{AU}_1$ can be obtained immediately. The proof of the proposition is complete. $\square$

Proof of Proposition 5

If $\alpha \leqslant \frac{1}{2}$, $\mathrm {IV_1}=0$. If $\alpha >\frac{1}{2}$, $\mathrm{{IV_1}}=(2\alpha -1)(1-F(\theta _1))a_1+\int ^{\theta _1}_{\underline{\theta }}{F(\theta )}\mathrm {d}\theta \geqslant 0.$ Differentiating $\mathrm {IV_1}$ with respect to $\alpha$ yields

$$\begin{aligned} \frac{\mathrm {d}\mathrm {IV_1}}{\mathrm {d}\alpha }=2(1-F(\theta _1))a_1\geqslant 0, \end{aligned}$$

where the inequality follows from the fact that $a_1\geqslant 0$. Therefore, the proof of the proposition is complete. $\square$

Proof of Proposition 6

Similar to the Proof of Proposition 5. $\square$

Proof of Proposition 7

Similar to the Proof of Proposition 5. $\square$

Proof of Proposition 8

Similar to the Proof of Proposition 5. $\square$

Proof of Proposition 9

If $\alpha \leqslant \frac{1}{2}$, $\mathrm {IV_1=IV_2=EV_1=EV_2=0}$. If $\alpha >\frac{1}{2}$, $\mathrm {IV_1}-\mathrm {IV_ 2}= [1-F(\theta )][1-(1-(2\alpha -1)a_1)^2]+\int _{\underline{\theta }}^{\theta _1}F(\theta )[1-(2\alpha -1)a_1]\mathrm {d}\theta +\frac{1}{2}\int _{\underline{\theta }}^{\theta _1}h(\theta )^2 f(\theta )\mathrm {d}\theta \geqslant 0$ and $\mathrm {EV_1}-\mathrm {EV_2}\geqslant \frac{1}{2}-\frac{1}{2}[(1-(2\alpha -1)a_1)^2]+\frac{1}{2}\int _{\underline{\theta }}^{\theta _1}(1+h(\theta )^2)f(\theta )\mathrm {d}\theta \geqslant 0$. Furthermore, $\mathrm {EV_2}-\mathrm {IV_1}\geqslant (2\alpha -1)a_1\left[ 1-\frac{1}{2}(2\alpha -1)a_1F(\theta )\right] \geqslant 0$, so that $\mathrm {EV_1}\geqslant \mathrm {EV_2} \geqslant \mathrm {IV_1} \geqslant \mathrm {IV_2}\geqslant 0$. Therefore, the proof of the proposition is complete. $\square$

Proof of Proposition 10

If $\alpha \leqslant \frac{1}{2}$, by differentiating the firm’s profits with respect to $a_1$ and $a_2$ in four information cases, we obtain $\partial \pi _F^{SO}/\partial a_1=\partial \pi _F^{SU}/\partial a_1=\partial \pi _F^{AO}/\partial a_1=\partial \pi _F^{AU}/\partial a_1=1-2\alpha \geqslant 0$ and $\partial \pi _F^{SO}/\partial a_2=\partial \pi _F^{SU}/\partial a_2=\partial \pi _F^{AO}/\partial a_2=\partial \pi _F^{AU}/\partial a_2=2\alpha -1 \leqslant 0$, respectively. If $\alpha >\frac{1}{2}$, by differentiating the firm’s profits with respect to $a_2$ and $a_1$ in four information cases, we obtain $\partial \pi _F^{SO}/\partial a_1=0$, $\partial \pi _F^{SU}/\partial a_1=(1-2\alpha )((1-2\alpha )a_1-1)<0$, $\partial \pi _F^{AO}/\partial a_1=(1-2\alpha )(1-F(\theta ))<0$, $\partial \pi _F^{AU}/\partial a_1<(1-2\alpha )(1-F(\theta ))<0$ and $\partial \pi _F^{SO}/\partial a_2=\partial \pi _F^{SU}/\partial a_2=\partial \pi _F^{AO}/\partial a_2=\partial \pi _F^{AU}/\partial a_2=2\alpha -1>0$, respectively. Therefore, the proof of the proposition is complete. $\square$

Proof of Proposition 11

Similar to the Proof of Proposition 10.$\square$