Dynamic pricing and production control for perishable products under uncertain environment

Abstract

In actual dynamic system, uncertainty is absolute and certainty is relative. This paper presents the optimal dynamic pricing and production control strategy for perishable products in finite horizon. The influence of external environmental disturbance on the system is considered by means of a special uncertain process (Liu process). Then based on uncertainty theory and Hurwicz criterion, the optimization model is built, where control variables are restricted to an admissible control set. In addition, uncertain differential equation is used to describe the changes of inventory. By applying the optimality equation, we determine the optimal price and production strategy to maximize profit. Besides, both the optimal price and production rate are linearly decreasing with inventory. Afterwards, two numerical examples are given, the results reveal that reducing the uncertain disturbance of inventory and expanding the potential market size are beneficial to improving the optimal profit. Moreover, risk-loving decision makers can gain more profits while facing large risks.

Appendices

Appendix A. Matlab procedure for solving $X_{t}^{\alpha}$

Take $X_t\ge 0$, for example, the $\alpha -$path $X_{t}^{\alpha}$ satisfies the ordinary differential equation:

$$\begin{aligned} {\rm{d}}X^\alpha _t= \Big (\big (4aQ(t)-\theta \big )X_{t}^{\alpha} +2aM(t)-\frac{\mu }{2} +\sigma \frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\Big ){\rm{d}}t, \end{aligned}$$

(A.1)

where $Q(t)=\frac{\theta }{4a}+ \frac{\sqrt{a m}(\zeta e^{4\sqrt{a m}(t-T)}-1)}{2a(1+\zeta e^{4\sqrt{a m}(t-T)})},\, M(t)=\frac{\mu -2\lambda }{4a}\Big (1-\frac{\theta }{2\sqrt{am}}\Big ) \frac{ e^{4\sqrt{am}(t-T)}-2 e^{2\sqrt{am}(t-T)}+1}{\zeta e^{4\sqrt{am}(t-T)}+1}.$ Due to the complexity of differential equation (A.1), it is difficult for us to directly derive the analytical form of $X_{t}^{\alpha}$, so the mathematical software MATLAB is helpful. In Matlab, ’dsolve’ function is used to calculate the ordinary differential equation directly, and the analytic form of $X_{t}^{\alpha}$ can be obtained.

For convenience, we use some symbols to represent parameters in MATLAB as follows,

$$\begin{aligned} Xta=X_{t}^{\alpha} ,\,\,alp=\alpha ,\,\,the=\theta ,\,\,ze=\zeta ,\,\,mu=\mu ,\,\,lam=\lambda ,\,\,sig=\sigma ,\,\,X0=X_0. \end{aligned}$$

We apply ’dsolve’ function directly to the differential equation (A.1), and the procedure is

$$\begin{aligned}{} & Xta=dsolve('Dy=(4*a*(the/(4*a)+sqrt(a*m)*(ze*exp(4*sqrt(a*m)*(t-T))-1)\\&/(2*a*(1+ze*exp(4*sqrt(a*m)*(t-T)))))-the)*y\\&+2*a*((mu-2*lam)/(4*a)*(1-the/(2*sqrt(a*m)))*(exp(4*sqrt(a*m)*(t-T))\\&-2*exp(2*sqrt(a*m)*(t-T))+1)/(ze*exp(4*sqrt(a*m)*(t-T))+1))\\&-mu/2+sig*sqrt(3)/pi*log(alp/(1-alp))','y(0)=X0'). \end{aligned}$$

After running, the analytical form of $X_{t}^{\alpha}$ is available. The distribution and inverse distribution of uncertain inventory can be obtained by substituting the values of each parameter.

Appendix B. Numerical algorithms for $X_t,\,p(t),\,u(t)$

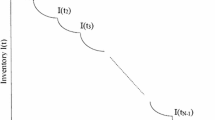
For $T=[0,6]$, set $0=t_0<t_1<\cdots <t_{600}=6$, and $\Delta t=0.01$. Then, if $X_t\ge 0$, the uncertain differential equation (6.1) transforms as $\Delta X_t=\Big ((4aQ(t)-\theta )\Delta X_t+2aM(t)-\frac{\mu }{2}\Big )\Delta t+ \sigma \Delta C_t;$ otherwise, $\Delta X_t=\Big (4aQ_1(t)\Delta X_t+2aM_1(t)-\frac{\mu }{2}\Big )\Delta t+ \sigma \Delta C_t.$

According to Jiang et al. (2016), the normal uncertain variable $\Delta C_t$ has a sample point $\widetilde{c}_t$, where $\widetilde{c}_t= \frac{\sqrt{3}\Delta t}{-\pi }\ln \Big ( \frac{1}{rand(0,1)}-1\Big )$. Then, for $X_t\ge 0$,

$$\begin{aligned} x_{t_{i+1}}=x_{t_i}+\Big [(4aQ(t_i)-\theta )x_{t_i}+2aM(t_i)-\frac{\mu }{2}\Big ]\triangle t+ \sigma \frac{\sqrt{3}\Delta t}{-\pi }\ln \Big ( \frac{1}{rand(0,1)}-1\Big ),\\ p(t_i)=Q(t_i)x_{t_i}+\frac{M(t_i)}{2}+\frac{\mu }{2b},\, \, u(t_i)=\frac{Q(t_i)}{c}x+\frac{M(t_i)}{2c}, \end{aligned}$$

and for $X_t<0$,

$$\begin{aligned} x_{t_{j+1}}=x_{t_j}+\Big [4aQ_1(t_j)x_{t_j}+2aM_1(t_j)-\frac{\mu }{2}\Big ]\Delta t+ \sigma \frac{\sqrt{3}\Delta t}{-\pi }\ln \Big ( \frac{1}{rand(0,1)}-1\Big ),\\ p(t_i)=Q_1(t_j)x_{t_j}+\frac{M_1(t_i)}{2}+\frac{\mu }{2b},\, \, u(t_i)=\frac{Q_1(t_j)}{c}x+\frac{M_1(t_j)}{2c}. \end{aligned}$$

By iterative calculation, some data are listed in Table 2.