Skip to main content
Springer Nature Link
Log in

A hierarchical genetic algorithm approach for curve fitting with B-splines

  • Published:
Genetic Programming and Evolvable Machines Aims and scope Submit manuscript

Abstract

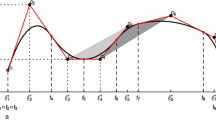
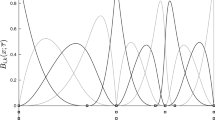
Automatic curve fitting using splines has been widely used in data analysis and engineering applications. An important issue associated with data fitting by splines is the adequate selection of the number and location of the knots, as well as the calculation of the spline coefficients. Typically, these parameters are estimated separately with the aim of solving this non-linear problem. In this paper, we use a hierarchical genetic algorithm to tackle the B-spline curve fitting problem. The proposed approach is based on a novel hierarchical gene structure for the chromosomal representation, which allows us to determine the number and location of the knots, and the B-spline coefficients automatically and simultaneously. Our approach is able to find optimal solutions with the fewest parameters within the B-spline basis functions. The method is fully based on genetic algorithms and does not require subjective parameters like smooth factor or knot locations to perform the solution. In order to validate the efficacy of the proposed approach, simulation results from several tests on smooth functions and comparison with a successful method from the literature have been included.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Notes

  1. The source files for the BARS algorithm were coded in C with wrapper to R software [21] and can be downloaded from http://www.stat.cmu.edu/~kass/bars/bars.html. See [25] for a complete description of this algorithm.

References

  1. H. Akaike, A new look at the statistical model identification. IEEE Trans. Autom. Control 19, 716–723 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  2. M. Bessaou, A. Pétrowski, P. Siarry, in PPSN VI: Proceedings of the 6th International Conference on Parallel Problem Solving from Nature. Island Model Cooperating with Speciation for Multimodal Optimization (Springer, Berlin, 2000), pp. 437–446

  3. K. Deb, R.B. Agrawal, Simulated binary crossover for continuous search space. Complex Syst. 9, 115–148 (1995)

    MATH  MathSciNet  Google Scholar 

  4. C. De Boor, A Practical Guide to Splines (Springer, New York, 1978)

    Book  MATH  Google Scholar 

  5. C. De Boor, On calculating with B-spline. J. Approx. Theory 6, 50–62 (1972)

    Article  MATH  Google Scholar 

  6. D.G.T. Denison, B.K. Mallick, A.F.M. Smith, Automatic Bayesian curve fitting. J. R. Stat. Soc. Ser. B Stat. Methodol. 60, 333–350 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  7. I. Dimatteo, C.R. Genovese, R.E. Kass, Bayesian curve-fitting with free-Knot splines. Biometrika 88(4), 1055–1071 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  8. J.H. Friedman, Multivariate adaptive regression splines (with discussion). Ann. Stat. 19(1), 1–141 (1991)

    Article  MATH  Google Scholar 

  9. J.H. Friedman, B.W. Silverman, Flexible parsimonious smoothing and additive modeling. Technometrics 31, 3–39 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  10. A. Gálvez, A. Iglesias, Efficient particle swarm optimization approach for data fitting with free knot B-splines. Comput. Aided Des. 43(12), 1683–1692 (2011)

    Article  Google Scholar 

  11. D.E. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning (Addison-Wesley Professional, Boston, MA, 1989)

  12. T.J. Hastie, R.J. Tibshirani, Generalized Additive Models (Chapman & Hall CRC, London, 1990)

    MATH  Google Scholar 

  13. J.H. Holland, Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence (The MIT Press, Cambridge, 1992)

    Google Scholar 

  14. J.Y. Koo, Spline estimation of discontinuous regression functions. J. Comput. Graph. Stat. 6, 266–284 (1997)

    MathSciNet  Google Scholar 

  15. T.C.M. Lee, Smoothing parameter selection for smoothing splines: a simulation study. Comput. Stat. Data Anal. 42(1–2), 139 (2003)

    Article  MATH  Google Scholar 

  16. T.C.M. Lee, On algorithms for ordinary least squares regression spline fitting: a comparative study. J. Stat. Comput. Simul. 72(8), 647–663 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  17. T.C.M. Lee, Regression spline smoothing using the minimum description length principle. Stat. Probab. Lett. 48(1), 71–82 (2000)

    Article  MATH  Google Scholar 

  18. K.-F. Man, K.-S. Tang, S. Kwong, Genetic Algorithms: Concepts and Designs with Disk (Springer-Verlag New York Inc, Secaucus, 1999)

    Book  Google Scholar 

  19. L. Pingping, Z. Xiuyang, Y. Bo, in International Conference on Future Computer and Communication (ICFCC). Automatic Knot Adjustment by an Improved Genetic Algorithm, vol. 3, pp. 763–768 (2010)

  20. J. Pittman, Adaptive splines and genetic algorithms. J. Comput. Graph. Stat. 11(3), 615–638 (2002)

    Article  MathSciNet  Google Scholar 

  21. R Development Core Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, ISBN: 3-900051-07-0, http://www.R-project.org (2009)

  22. M. Smith, R. Kohn, Nonparametric regression using Bayesian variable selection. J. Econ. 75(2), 317–343 (1996)

    Article  MATH  Google Scholar 

  23. M. Tomassini, Spatially Structured Evolutionary Algorithms: Artificial Evolution in Space and Time (Natural Computing Series) (Springer-Verlag New York Inc, Secaucus, 2005)

    Google Scholar 

  24. G. Wahba, Spline Models for Observational Data, SIAM [Society for Industrial and Applied Mathematics], vol. 169 (1990)

  25. G. Wallstrom, J. Liebner, R.E. Kass, An implementation of Bayesian adaptive regression splines (BARS) in C with S and R wrappers. J. Stat. Softw. 26(1), 1–21 (2007)

    Google Scholar 

  26. F. Yoshimoto, T. Harada, Y. Yoshimoto, Data fitting with a spline using a real-coded genetic algorithm. Comput. Aided Des. 35(8), 751–760 (2003)

    Article  Google Scholar 

  27. F. Yoshimoto, M. Moriyama, T. Harada, in Proceedings of the International Conference on Shape Modeling and Applications. Automatic Knot Placement by a Genetic Algorithm for Data Fitting with a Spline (IEEE Computer Society Press, 1999), pp. 162–169

  28. M. Zamani, A simple piecewise cubic spline method for approximation of highly nonlinear data. Nat. Sci. 4, 79–83 (2012)

    Google Scholar 

  29. X. Zhao, C. Zhang, B. Yang, P. Li, Adaptive knot placement using a GMM-based continuous optimization algorithm in B-spline curve approximation. Comput. Aided Des. 43(6), 598–604 (2011)

    Article  Google Scholar 

Download references

Acknowledgments

We acknowledge the support of the Consejo Nacional de Ciencia y Tecnología de México, Centro de Investigaciones en Óptica, A.C. and Instituto Tecnológico Superior de Irapuato. This work has been partially funded by the CONACYT Project 229839 (Apoyo al Fortalecimiento y Desarrollo de la Infraestructura Científica y Tecnológica 2014) and the DAIP Project 444 (Convocatoria Institucional de Investigación Científica 2014).

Author information

Authors and Affiliations

  1. Department of Optical Metrology, Centro de Investigaciones en Óptica, A.C., Loma del Bosque 115, Col. Lomas del Campestre, 37150, León, Guanajuato, Mexico

    C. H. Garcia-Capulin & F. J. Cuevas

  2. Department of Mechatronics, Instituto Tecnológico Superior de Irapuato, Carr. Irapuato-Silao Km. 12.5, 36821, Irapuato, Guanajuato, Mexico

    G. Trejo-Caballero

  3. Department of Electronics, DICIS - Universidad de Guanajuato, Com. Palo Blanco s/n, 36885, Salamanca, Guanajuato, Mexico

    H. Rostro-Gonzalez

Authors
  1. C. H. Garcia-Capulin
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. F. J. Cuevas
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. G. Trejo-Caballero
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. H. Rostro-Gonzalez
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to C. H. Garcia-Capulin.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Garcia-Capulin, C.H., Cuevas, F.J., Trejo-Caballero, G. et al. A hierarchical genetic algorithm approach for curve fitting with B-splines. Genet Program Evolvable Mach 16, 151–166 (2015). https://doi.org/10.1007/s10710-014-9231-3

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10710-014-9231-3

Keywords