Abstract
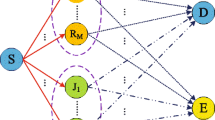
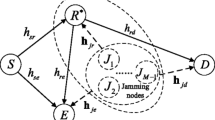
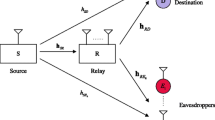
To enhance the physical-layer security of a decode-and-forward (DF) cooperative relay network in the presence of a potential eavesdropper, a joint relay selection and destination assisted cooperative jamming (CJ) scheme is proposed. In phase I, the source transmits its confidential signal, and concurrently, it cooperates with the friendly jammers and the destination to send jamming signals to confuse the eavesdropper without affecting the forwarding relay which is preselected. In phase II, the forwarding relay retransmits the decoded signal, and simultaneously, the particular relay cooperates with the friendly jammers to send jamming signal to confuse the eavesdropper without affecting the destination. The achievable secrecy rate maximization (SRM) problem is investigated by optimally allocating the power between the data signal and jamming signals. Although SRM problem is non-convex, the power allocation problem can be solved by a bisection method together with a one-dimensional search. Optimal relay selection and suboptimal relay selection schemes are also proposed to further improve the secrecy rate. Simulation results are presented to show that the joint scheme can attain higher achievable secrecy rates than some existing works.




Similar content being viewed by others
References
A. D. Wyner, The wire-tap channel, Bell System Technical Journal, Vol. 54, No. 8, pp. 1355–1387, 1975.
S. Leung-yan-cheong and M. E. Hellman, The Gaussian wire-tap channel, IEEE Transactions on Information Theory, Vol. 24, No. 4, pp. 451–456, 1978.
Y. Liang, H. V. Poor and S. Shamai, Secure communication over fading channels, IEEE Transactions on Information Theory, Vol. 54, No. 6, pp. 2470–2492, 2008.
P. K. Gopala, L. Lai and H. E. Gamal, On the secrecy capacity of fading channels, IEEE Transactions on Information Theory, Vol. 54, No. 10, pp. 4687–4698, 2008.
Shafiee S., Ulukus S., 2007. Achievable rates in Gaussian MISO channels with secrecy constraints. Proceeding of IEEE ISIT, Nice, France: IEEE Press, 2466–2470.
K. Cumanan, Z. Ding, B. Sharif, et al., Secrecy rate optimizations for a MIMO secrecy Channel with a multiple-antenna eavesdropper, IEEE Transactions on Vehicular Technology, Vol. 63, No. 4, pp. 1678–1690, 2014.
L. X. Li, Z. Chen, D. Zhang, et al., A full-duplex Bob in the MIMO Gaussion wiretap channel: scheme and performance, IEEE Signal Processing Letters, Vol. 23, No. 1, pp. 107–111, 2016.
H. Zhao, Y. Tan, G. Pan and Y. Chen, Ergodic secrecy capacity of MRC/SC in SIMO wiretap systems with imperfect CSI, Frontiers of Information Technology & Electronic Engineering., Vol. 18, No. 4, pp. 578–590, 2016.
S. Gerbracht, C. Scheunert and E. A. Jorswieck, Secrecy outage in MISO systems with partial channel information, IEEE Transactions on Information Forensics and Security, Vol. 7, No. 2, pp. 704–716, 2012.
Lun, D., Zhu, H., Petropulu, A.P., et al., 2009. Amplify-and-forward based cooperation for secure wireless communications. Proceeding of IEEE International Conference Acoustics Speech Signal Processing, Taipei, Taiwan, 2613–2616.
H. M. Wang, Q. Yin and X. G. Xia, Distributed beamforming for physical-layer security of two-way relay networks, IEEE Transactions on Signal Processing, Vol. 60, No. 7, pp. 3532–3545, 2012.
D. Lun, H. Zhu, A. P. Petropulu, et al., Improving wireless physical layer security via cooperating relays, IEEE Transactions on Signal Processing, Vol. 58, No. 3, pp. 1875–1888, 2010.
Y. Yang, Q. Li, W. K. Ma, P. C. Ching, et al., Cooperative secure beamforming for AF relay networks with multiple eavesdroppers, IEEE Signal Processing Letters, Vol. 20, No. 1, pp. 35–38, 2013.
Y. L. Zou, X. B. Wang and W. Shen, Optimal relay selection for physical-layer security in cooperative wireless networks, IEEE Journal on Selected Areas in Communications, Vol. 31, No. 10, pp. 2099–2111, 2013.
C. Wang, H. Wang and X. G. Xia, Hybrid opportunistic relaying and jamming with power allocation for secure cooperative networks, IEEE Transactions on Wireless Communications, Vol. 14, No. 2, pp. 589–605, 2015.
Zheng Gan, L. C. Choo and K. K. Wong, Optimal cooperative jamming to enhance physical layer security using relays, IEEE Transactions on Signal Processing, Vol. 59, No. 3, pp. 1317–1322, 2011.
J. P. Vilela, M. Bloch, J. Barros and S. W. Mclaughlin, Wireless secrecy regions with friendly jamming, IEEE ransactions on Information Forensics and Security, Vol. 6, No. 2, pp. 256–266, 2011.
S. Luo, L. I. Jiang-yuan and A. P. Petropulu, Uncoordinated cooperative jamming for secret communications, IEEE Transactions on Information Forensics and Security, Vol. 8, No. 7, pp. 1081–1090, 2013.
M. Lin, J. Ge and Y. Yang, An effective secure transmission scheme for AF relay networks with two-hop information leakage, IEEE Communications Letters, Vol. 17, No. 8, pp. 1676–1679, 2013.
Vishwakarma, S., Chockalingam, A., 2013. Amplify-and-forward relay beamforming for secrecy with cooperative jamming and imperfect CSI. Proceeding of IEEE International Conference on Communications, Budapest, Hungary, 3047–3052.
H. M. Wang, M. Luo, X. G. Xia and Q. Yin, Joint cooperative beamforming and jamming to secure AF relay systems with individual power constraint and no eavesdropper’s CSI, IEEE Signal Processing Letters, Vol. 20, No. 1, pp. 39–42, 2013.
H. Hui, A. L. Swindlehurst, G. Li and J. Liang, Secure relay and jammer selection for physical layer security, IEEE Signal Processing Letters, Vol. 22, No. 8, pp. 1147–1151, 2015.
J. C. Chen, R. Q. Zhang, L. Y. Song, Z. Han, et al., Joint relay and jammer selection for secure two-way relay networks, IEEE Transactions on Information Forensics and Security, Vol. 7, No. 1, pp. 310–320, 2012.
J. Y. Li, A. P. Petropulu and S. Weber, On cooperative relaying schemes for wireless physical layer security, IEEE Transactions on Signal Processing, Vol. 59, No. 10, pp. 4985–4997, 2011.
K. H. Park, T. Wang and M. S. Alouini, On the jamming power allocation for secure amplify-and-forward relaying via cooperative jamming, IEEE Journal on Selected Areas in Communications, Vol. 31, No. 9, pp. 1741–1750, 2013.
Y. Liu, J. Li and A. P. Petropulu, Destination assisted cooperative jamming for wireless physical-layer security, IEEE Transactions on Information Forensics and Security, Vol. 8, No. 4, pp. 682–694, 2013.
H. M. Wang, F. Liu and M. C. Yang, Joint cooperative beamforming, jamming, and power allocation to secure AF relay systems, IEEE Transactions on Vehicular Technology, Vol. 64, No. 10, pp. 4893–4898, 2015.
D. Tse and P. Viswanath, Fundamentals of wireless communication, Cambridge Univ. PressCambridge, 2005.
B. Friedlander and B. Porat, Performance analysis of a null-steering algorithm based on direction of arrival estimation, IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 37, No. 4, pp. 461–466, 1989.
S. Boyd and L. Vandenberghe, Convex optimization, Cambridge Univ. PressCambridge, 2004.
Funding
Project (HIT. MKSTISP. 2016 13) supported by the Fundamental Research Funds for the Center University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Derivation of Lemma 1
Denote \( f_{1} (P^{\prime}_{S} ,{\mathbf{w^{\prime}}}_{1} ) = \log_{2} \left( {\frac{{1 + P^{\prime}_{S} \left| {h_{SR} } \right|^{2} }}{{1 + \frac{{P^{\prime}_{S} \left| {h_{SE} } \right|^{2} }}{{1 + \left| {{\mathbf{w^{\prime}}}_{1}^{\dag } {\mathbf{h}}_{1} } \right|^{2} }}}}} \right), \) and \( f_{2} (P^{\prime}_{S} ,{\mathbf{w^{\prime}}}_{1} ,P^{\prime}_{R} ,{\mathbf{w^{\prime}}}_{2} ) = \log_{2} \left( {\frac{{1 + P^{\prime}_{R} \left| {h_{RD} } \right|^{2} }}{{1 + \frac{{P^{\prime}_{S} \left| {h_{SE} } \right|^{2} }}{{1 + \left| {{\mathbf{w^{\prime}}}_{1}^{\dag } {\mathbf{h}}_{1} } \right|^{2} }} + \frac{{P^{\prime}_{R} \left| {h_{RE} } \right|^{2} }}{{1 + \left| {{\mathbf{w^{\prime}}}_{2}^{\dag } {\mathbf{h}}_{2} } \right|^{2} }}}}} \right). \) Since \( P_{S} \) can be fixed, \( f_{1} (P_{S} ,{\mathbf{w}}_{1} ) \) is a strictly increasing function of \( \left\| {{\mathbf{w}}_{1} } \right\|^{2} . \) Consequently, if \( P^{\prime}_{S} + \left\| {{\mathbf{w^{\prime}}}_{1} } \right\|^{2} < P_{1} , \) there exists \( (P^{\prime}_{S} ,{\mathbf{w^{\prime}}}_{3} ), \)\( \left\| {{\mathbf{w^{\prime}}}_{3} } \right\|^{2} > \left\| {{\mathbf{w^{\prime}}}_{1} } \right\|^{2} \) such that \( f_{1} (P^{\prime}_{S} ,{\mathbf{w^{\prime}}}_{3} ) > f_{1} (P^{\prime}_{S} ,{\mathbf{w^{\prime}}}_{1} ). \) This contradicts the assumption that \( (P^{\prime}_{S} ,{\mathbf{w^{\prime}}}_{1} ) \) is optimum. Thus, it holds that \( P^{\prime}_{S} + \left\| {{\mathbf{w^{\prime}}}_{1} } \right\|^{2} = P_{1} . \) Similarly, we may show \( P^{\prime}_{R} + \left\| {{\mathbf{w^{\prime}}}_{2} } \right\|^{2} < P_{0} - P_{1} \) is impossible. This completes the proof.
Appendix 2: Derivation of Lemma 2
Before proceeding, we denote the objective function of (15) as \( H(P_{R} ) \). It is easy to see that the problem of (15) is an optimization problem of a single \( P_{R} \) variable, and the maximum is achieved at one of the following points: 0, \( P_{0} - P_{1} \) and the points with zero derivative of \( H(P_{R} ) \)\( \left( {H^{\prime}(P_{R} ) = 0} \right). \) And we have the following property w.r.t. \( H^{\prime}(P_{R} ). \)
Property 1
Whenever function \( H^{\prime}(P_{R} ) \) crosses the value 0 at any point belongs to \( [0,P_{0} - P_{1} ], \) we must have \( H^{\prime\prime}(P_{R} ) < 0 \) at this point.
Proof
The first- and the second-derivatives of \( H(P_{R} ) \) are respectively given by
and hence
If \( H^{\prime}(P_{R}^{*} ) = 0 \) with \( P_{R}^{*} \in [0,P_{0} - P_{1} ], \) then we have
Note that \( fP_{R}^{*} - s \le f(P_{0} - P_{1} ) - ((P_{0} - P_{1} )f + 1) < 0, \) then we must have \( H^{\prime\prime}(P_{R}^{*} ) < 0. \) This completes the proof. Based on the above property, we could also have the following result stated in Property 2.
Property 2
\( H^{\prime}(P_{R} ) \) could only have the following behaviors over \( P_{R} \in [0,P_{0} - P_{1} ] \)
-
i.
If \( H^{\prime}(P_{R} ) \) cross the value 0 at point \( P_{R}^{*} \in [0,P_{0} - P_{1} ], \) \( P_{R}^{*} \) must be unique. And for \( P_{R} \in [0,P_{R}^{*} ], \) we have \( H^{\prime}(P_{R} ) > 0; \) for \( P_{R} \in [P_{R}^{*} ,P_{0} - P_{1} ], \) we have \( H^{\prime}(P_{R} ) < 0. \)
-
ii.
If \( H^{\prime}(P_{R} ) \) does not cross the value 0 at all, \( H^{\prime}(P_{R} ) > 0 \) or \( H^{\prime}(P_{R} ) < 0 \) in \( [0,P_{0} - P_{1} ]. \)
Proof
First, we claim that if \( H^{\prime}(P_{R} ) \) crosses the value 0, it can cross the value 0 at most once. To see why this is the case, we should note that \( H^{\prime}(P_{R} ) \) is quadratic w.r.t \( P_{R} , \) it cannot cross value 0 more than twice. Thus, we assume that \( H^{\prime}(P_{R} ) \) crosses the value 0 twice at the two points \( 0 \le P_{R}^{*} < \tilde{P}_{R}^{*} \le P_{0} - P_{1} . \) From Property 1, we know that \( H^{\prime\prime}(P_{R}^{*} ) < 0 \) and \( H^{\prime\prime}(\tilde{P}_{R}^{*} ) < 0 \). According to the continuity of \( H^{\prime}(P_{R} ) \), there exists a very small \( \sigma > 0 \) such that \( H^{\prime}(P_{R}^{*} + \sigma ) < 0 \) and \( H^{\prime}(\tilde{P}_{R}^{*} - \sigma ) > 0 \). From the intermediate value theorem, we know that there is at least another one point \( \bar{P}_{R}^{*} \in \left[ {P_{R}^{*} ,\tilde{P}_{R}^{*} } \right] \) that makes \( H^{\prime}(\bar{P}_{R}^{*} ) = 0 \) and \( H^{\prime\prime}(\bar{P}_{R}^{*} ) > 0 \) (otherwise \( H^{\prime}(P_{R} ) \) cannot cross value 0), which contradicts the assumption that \( H^{\prime}(P_{R} ) \) crosses value 0 twice and Property 1. Therefore it should cross 0 exactly once. If \( H^{\prime}(P_{R} ) \) crosses the value 0 at point \( P_{R}^{*} \in [0,P_{0} - P_{1} ] \), because \( H^{\prime\prime}(P_{R}^{*} ) < 0 \), we know that \( H^{\prime}(P_{R} ) > 0 \) for \( P_{R} \in [0,P_{R}^{*} ] \) and \( H^{\prime}(P_{R} ) < 0 \) for \( P_{R} \in [P_{R}^{*} ,P_{0} - P_{1} ] \).
If \( H^{\prime}(P_{R} ) \) does not cross the value 0 at all, it is obviously that \( H^{\prime}(P_{R} ) > 0 \) or \( H^{\prime}(P_{R} ) < 0 \) in \( [0,P_{0} - P_{1} ] \). This completes the proof of Property 2.
If \( H^{\prime}(0) > 0 \) and \( H^{\prime}(P_{0} - P_{1} ) < 0 \), according to Property 2 (i) \( H^{\prime}(P_{R} ) \) crosses the value 0 at the unique point \( P_{R}^{*} \in [0,P_{0} - P_{1} ] \), \( H^{\prime}(P_{R} ) > 0 \), i.e., \( H(P_{R} ) \) is increasing for \( P_{R} \in [0,P_{R}^{*} ] \), and \( H^{\prime}(P_{R} ) < 0 \), i.e., \( H(P_{R} ) \) is decreasing for \( P_{R} \in [P_{R}^{*} ,P_{0} - P_{1} ] \), so \( H(P_{R} ) \) attains its maximum at \( P_{R} = P_{R}^{*} \). To obtain the exact value of \( P_{R}^{*} \), let \( H^{\prime}(P_{R} ) = 0 \), and we get an equation
The solution to (27) is \( \frac{{ - B_{1} \pm \sqrt {B_{1}^{2} - 4A_{1} C_{1} } }}{{2A_{1} }} \), while \( \frac{{ - B_{1} }}{{2A_{1} }} = \frac{{2\left[ {1 + f\left( {P_{0} - P_{1} } \right)} \right]}}{f - g} \ge 2\left( {\frac{1}{f} + P_{0} - P_{1} } \right), \) thus \( P_{R}^{*} = \frac{{ - B_{1} - \sqrt {B_{1}^{2} - 4A_{1} C_{1} } }}{{2A_{1} }} \) should be the only choice. This means if \( H^{\prime}(0) > 0 \) and \( H^{\prime}(P_{0} - P_{1} ) < 0 \), the solution of (15) is \( G(P_{S} ) = \frac{{ - B_{1} - \sqrt {B_{1}^{2} - 4A_{1} C_{1} } }}{{2A_{1} }} \).
If \( H^{\prime}(0) < 0 \) and \( H^{\prime}(P_{0} - P_{1} ) > 0 \), there must be a point \( P_{R}^{*} \in [0,P_{0} - P_{1} ] \) with \( H^{\prime}(P_{R}^{*} ) = 0 \) that makes \( H^{\prime\prime}(P_{R}^{*} ) > 0 \), which contradicts with Property 1, thus this case is impossible.
If \( H^{\prime}(P_{0} - P_{1} ) > 0 \) and \( H^{\prime}(0) > 0 \), it is obviously \( H^{\prime}(P_{R} ) \) cannot crosses value 0 exactly once, according to Property 2, we can obtain that \( H^{\prime}(P_{R} ) > 0 \), i.e., \( H(P_{R} ) \) is strictly increasing on \( [0,P_{0} - P_{1} ] \), and its maximum happens to be \( H(P_{0} - P_{1} ) \), i.e., \( G(P_{S} ) = P_{0} - P_{1} \).
Similarly, if \( H^{\prime}(P_{0} - P_{1} ) < 0 \) and \( H^{\prime}(0) < 0 \), we can obtain that \( H^{\prime}(P_{R} ) < 0 \), i.e., \( H(P_{R} ) \) is strictly decreasing on \( [0,P_{0} - P_{1} ] \). The maximum value is \( H(0) = \frac{1}{1 + m} < 1 \), which implies that the secrecy rate is negative. In this case, the security of the system cannot be guaranteed.
This completes the proof.
Appendix 3: Derivation of Lemma 3
Now we first show \( J_{2} (P_{S} ) \) is a strictly decreasing function of \( P_{S} \).
If \( G(P_{S} ) = P_{0} - P_{1} , \) then \( J_{2} (P_{S} ) = \frac{{1 + d(P_{0} - P_{1} )}}{{1 + m + e(P_{0} - P_{1} )}}. \) It is easy to see that \( J_{2} (P_{S} ) \) decreases with \( m \). Since \( m \) increases with \( P_{S} \), then \( J_{2} (P_{S} ) \) is decreasing function of \( P_{S} \).
If \( G(P_{S} ) = 0 \), then \( J_{2} (P_{S} ) = \frac{1}{1 + m} \). Thus in this case \( J_{2} (P_{S} ) \) is still a decreasing function of \( P_{S} \).
Finally, if \( G(P_{S} ) = \frac{{ - B_{1} - \sqrt {B_{1}^{2} - 4A_{1} C_{1} } }}{{2A_{1} }} \), substituting (18b)–(18d) into (17), we can transform \( g \) into a function of \( G(P_{S} ) \).
where \( P_{2} = P_{0} - P_{1} \). We now have
Substitue (28) into (29), we can further obtain
Since \( G\text{(}P_{S} \text{)} \in [0,P_{2} ] \), \( J_{2} (P_{S} ) \) monotonically increases with \( G(P_{S} ) \), and we know that \( G(P_{S} ) \) decreases with \( P_{S} \). As a result, \( J_{2} (P_{S} ) \) decreases with \( P_{S} \).
From the above three cases, we conclude that \( J_{2} (P_{S} ) \) is strictly decreasing and thus quasi-concave. Due to the convexity of \( J_{1} (P_{S} ) \) with fixed \( P_{1} \), \( J(P_{S} ) \) is a point-wise minimum of a family of affine functions, as a result quasi-concave [30]. And its maximum value can be obtained via a bisection method. This completes the proof.
Rights and permissions
About this article
Cite this article
Jia, S., Zhang, J., Zhao, H. et al. Joint Relay Selection and Destination Assisted Cooperative Jamming with Power Allocation for Secure DF Relay Network. Int J Wireless Inf Networks 26, 201–211 (2019). https://doi.org/10.1007/s10776-019-00442-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10776-019-00442-x