1 Introduction

Ranking is a common issue in many real world problems. For instance, students may be ranked by their GPA scores when applying for the scholarship; soccer teams can be ranked by a scoring system depending on how many matches they win and how many they lose. When considering the ranking problem in IR systems, the number of features becomes large, making the ranking task challenging. Thus, various ranking models were proposed in order to aggregate multiple features into a single ranking score, by which the documents can be properly ranked. Using the ranking model, a subset of documents with highest ranking scores is retrieved from the repository to satisfy users’ information needs expressed in queries. Classical ranking models include the Vector Space Model (Salton et al. 1975), the Okapi BM25 probabilistic model (Robertson et al. 1994) and language models (Cao et al. 2005). Term frequency (tf), inverse document frequency (idf) and document length (dl) are main features which come into play. With the advent of more complicated documents (e.g. web pages), a large quantity of new features are involved such as the link-based PageRank scores (Brin and Page 1998) and HITS scores (Kleinberg 1999), as well as structure-based features (title-based, metadata-based, anchor text-based etc.). Traditional ranking models often fails in handling these new IR scenarios, resulting in the introduction of machine learning technology for ranking.

The application of machine learning techniques in the ranking problem forms a specialized term “learning to rank”. Learning to rank employs machine learning techniques to automatically obtain the ranking model using a labeled training dataset. Much contribution has been made in developing advanced rank learning approaches. Existing approaches can be mainly categorized into three types, which are point-wise, pair-wise and list-wise, according to the different loss functions being optimized. The point-wise approaches (Li et al. 2007) degrade the ranking problem to classification by treating the document relevance rating as class label. The pair-wise approaches (Herbrich et al. 2000; Freund et al. 2003) explore the ordinal relationship between two documents and hence convert the ranking problem to a binary classification problem. Finally, the list-wise approaches (Fan et al. 2004a, b; Burges et al. 2006a; Xu and Li 2007; Cao et al. 2007) define a loss function on the entire document ranking list. It is notable that the pair-wise methods such as Ranking SVM (Herbrich et al. 2000) are the most prominent ones both in literature and practice.

Among various learning to rank algorithms, most of them belong to the supervised learning paradigm. It is highly costly to collect and label sufficient data for training purpose, since human labeler need to judge the relevance level of each query-document pair. As a result, the lack of labeled training data is very common in the practice of learning to rank. Fortunately, in some cases, we may get some additional imprecise labeled data, where imprecise means that they are not drawn from the same problem or domain as the future test data. For example, when training a ranking model for a search engine, large amounts of query-page pairs were previously labeled. After a period of time, these data may become outdated, since the distribution of queries submitted by users is time-varying. Here, these outdated data are treated as the imprecise training data. In another scenario, suppose a ranking model is desired for a newly born vertical search engine while only labeled data from another vertical search engine are available. These out-of-domain data are treated as the imprecise training data. Conclusively, both situations result in the cross domain learning to rank problem.

In this paper, our goal is to define and propose solutions to the cross domain learning to rank problem, i.e., to leverage useful knowledge from the imprecise data in order to enhance the performance of the learned ranking model for current ranking task. For clarity, we call the imprecise data as “source domain data”, while a small quantity of labeled data from current problem as “target domain data”. Evidently, the source domain data cannot be utilized directly in training a ranking model for the target domain due to the distribution difference. To address this, we theoretically study the cross domain learning to rank problem from two aspects: feature level and instance level. The feature-level transfer learning method assumes that there exists a low-dimensional feature representation shared by both source domain and target domain data, while the instance-level transfer learning method makes use of the source domain data by adapting each instance to the target domain from a probabilistic distribution view. Both the feature-level and instance-level transfer learning method are formalized as optimization problems which can then be solved by using Ranking SVM as the basic learner. In the experiments, we manually construct several cross domain learning to rank cases using benchmark datasets to validate the effectiveness and robustness of our proposed methods. Besides, we further hold a discussion section on our findings.

The paper is organized as follows. In Sect. 2, we formally define the learning to rank problem and further the cross domain learning to rank problem. A survey on transfer learning is also included. In Sect. 3, our proposed knowledge transfer methods are presented in detail. Finally, Sect. 4 gives our experimental details and Sect. 5 concludes our paper.

2 Problem formulation

2.1 Learning to rank

Recently, learning to rank is emerging as a new machine learning branch following the traditional classification, regression and clustering research. The difference between learning to rank and these problems is that it aims to construct a model which predicts the actual ranking of documents for a query as accurately as possible. From the machine learning perspective, the loss function in learning to rank takes into account the ordinal relationships between documents rather than the absolute label for a single document. Generally speaking, there are mainly three types of learning to rank approaches, which are point-wise, pair-wise and list-wise, respectively. Among these, the pair-wise approaches have been studied most intensively. Representative pair-wise methods include Ranking SVM (Herbrich et al. 2000), RankBoost (Freund et al. 2003), RankNet (Burges et al. 2006b) etc. In the following, we introduce the optimization formation of Ranking SVM which is accepted as one of the state-of-the-art pair-wise methods.

Ranking SVM was first proposed by R. Herbrich to solve the ordinal regression problem on the basis of classification SVM. It introduces the structural risk minimization principle into the learning to rank problem and achieves good performance in various applications. In this paper, we utilize Ranking SVM as the basic learner.

Suppose that there is an input space \({\boldsymbol{X}} \in {\boldsymbol {R}}^{d}, \) where d is the number of features. Generally, a set of pair-wise preferences \({\boldsymbol {S}} = \left\{ {\left( {{\boldsymbol {x}}_{i1},{\boldsymbol {x}}_{i2} } \right)} \right\}_{i = 1}^{n} \) is given as the training data. A pair (x i1, x i2) indicates that \( {\boldsymbol {x}}_{i1} \succ {\boldsymbol {x}}_{i2}, \) where \( \succ \) denotes a preference relationship. The learning process is to find a ranking model \( f \in {\boldsymbol {F}} \) which predicts the preference relationships as accurately as possible,

$$ {\boldsymbol {x}}_{i1} \succ {\boldsymbol {x}}_{i2} \Leftrightarrow \left( {{\boldsymbol {x}}_{i1} } \right) > f\left( {{\boldsymbol {x}}_{i2} } \right) $$
(1)

Further assume that f is a linear function with the regression parameter w,

$$f({\boldsymbol {x}}) = \left\langle {{\boldsymbol {w,x}}}\right\rangle $$
(2)

where \( \left\langle { \cdot , \cdot } \right\rangle \) stands for the inner product between two vectors. In Ranking SVM, learning to rank is formalized as a classification task on a new vector y i  = x i1 – x i2, by plugging (2) into (1),

$$ {\boldsymbol {x}}_{i1} \succ {\boldsymbol {x}}_{i2} \Leftrightarrow\left\langle {{\boldsymbol {w,y}}_{i} } \right\rangle > 0 $$
(3)

In this way, the training data are converted to S′ = {(y i , z i )} ni=1 , where z i  = 1 if \( {\boldsymbol {x}}_{i1} \succ {\boldsymbol {x}}_{i2}, \) and z i  = −1 otherwise. Now, the original learning to rank problem is equivalent to a binary classification task on S′, which is to construct a SVM model to predict either positive or negative label for each new vector y i . Here we use the pair-wise hinge loss function for learning to rank,

$$ l_{h} \left( {{\boldsymbol {w}};{\boldsymbol {y}}_{i} ,z_{i} }\right) = \left( {1 - z_{i} \left\langle {{\boldsymbol{w}},{\boldsymbol {y}}_{i} } \right\rangle } \right)_{ + } $$
(4)

The optimization problem can then be expressed as

$$ {\boldsymbol {w}}^{*} = \arg \min_{{\boldsymbol {w}}}\int\limits_{{{\boldsymbol {X}}^{2} \times {\boldsymbol {Z}}}}{l_{h} \left( {{\boldsymbol {w}};{\boldsymbol {y}},z} \right)D\left({{\text{d}}{\boldsymbol {y}},{\text{d}}z} \right)} $$
(5)

Under the assumption that the training and test data share the same data distribution, labeled training data are used to estimate D(dy, dz),

$$ {\boldsymbol {w}}^{*} = \arg \min_{\boldsymbol {w}} \sum\limits_{i =1}^{n} {l_{h} ({\boldsymbol {w}};{\boldsymbol {y}}_{i} ,z_{i} )} $$
(6)

To avoid overfitting and improve the generalization ability of the learned ranking model, Ranking SVM imports a penalty on model complexity,

$${\boldsymbol {w}}^{*} = \arg \min_{{\boldsymbol {w}}} \sum\limits_{i= 1}^{n} {l_{h} \left( {{\boldsymbol {w}};{\boldsymbol {y}}_{i},z_{i} } \right) + \lambda \left\| {\boldsymbol {w}} \right\|^{2} } $$
(7)

This optimization problem can be solved with either gradient descent or quadratic programming. In Joachims’ implementation,Footnote 1 the latter one is chosen and we use his tool in the experiments of this paper.

2.2 Cross domain learning to rank

In the configuration of cross domain learning to rank problem, two parts of labeled data are available. In other words, this is a supervised transfer learning problem. In this paper, we assume that the source domain and target domain data share a common document feature space \( {\boldsymbol {X}} \in {\boldsymbol {R}}^{d}, \) while the data distributions for them are different.

In learning to rank for information retrieval, training data are often given in the form of individual queries together with its related documents. Suppose we have two collections of labeled data denoted as \( {\boldsymbol {D}}_{s} = \left\{ {{\boldsymbol {Q}}_{s}^{(i)} }\right\}_{i = 1}^{{N_{s} }} \) from the source domain and \( {\boldsymbol {D}}_{t} = \left\{ {{\boldsymbol {Q}}_{t}^{(i)} }\right\}_{i = 1}^{{N_{t} }} \) from the target domain. Each Q stands for a subset of training data associated with a specific query, that is \( {\boldsymbol {Q}} = \left\{ {{\boldsymbol {x}}_{j} ,r_{j} }\right\}_{j = 1}^{{n_{Q} }} \) where r j is the relevance rating of document x j to the corresponding query. The pair-wise preferences are constructed within each Q based on the relevance ratings. Note that, the labeled data from source domain are more plentiful than those from target domain, i.e., \( N_{t} \ll N_{s}. \) The goal of cross domain learning to rank is to learn a ranking model f: R d → R for the target domain by exploiting the small-scale D t and the imprecise data D s .

2.3 Related work: transfer learning

The cross domain learning to rank idea borrows concept from transfer learning which has been successfully applied in many problems such as document classification. The techniques for transfer learning have attracted much attention since its first appearance in the NIPS workshop “Learning to Learn”Footnote 2 in 1995. The fundamental motivation of transfer learning is to apply the knowledge gained from one problem to a different but related problem. For example, learning to recognize apples might help to recognize pears; a programmer who has learned C++ might help to learn Java. Recently, transfer learning techniques have been intensively studied in machine learning and data mining areas. Among various literatures on transfer learning, there are two dominant types of approaches. One is instance weighting approaches where each source domain instance is weighted in certain way to adjust its importance during the training process. The other is common feature learning approaches where the useful knowledge in source domain is bridged to help the target domain task via several features.

The data distribution is different in source and target domain, that is P s (X, Y) ≠ P t (X, Y). Some instance weighting work (Lin et al. 2002; Chan and Ng 2005) assumes that \( P_{s} \left( {X\left| Y \right.} \right) = P_{t} \left( {X\left| Y \right.} \right) \) while P s (Y) ≠ P t (Y), called class imbalance. Lin et al. (2002) succeeded to adapt support vector machines to such nonstandard situations and validate their method via simulated experiments. Chan and Ng (2005) used P t (Y)/P s (Y) to weight instance in the domain adaptation problem in word sense disambiguation (WSD) using naive Bayes classifiers. Similarly, some instance weighting work (Sugiyama and Müller 2005; Huang et al. 2007) assumes that \( P_{s} \left( {Y\left| X \right.} \right) = P_{t} \left( {Y\left| X \right.} \right) \) while P s (X) ≠ P t (X), called covariate shift. Sugiyama and Müller (2005) used non-parametric kernel density estimation to estimate the ratio P t (X)/P s (X) for each instance, while Huang et al. (2007) transformed the problem into a kernel mean matching problem in a reproducing kernel Hilbert space. The last situation assumes that P s (X) = P t (X) while \( P_{s} \left( {Y\left| X \right.} \right) \ne P_{t} \left( {Y\left| X \right.} \right) \). Jiang and Zhai (2007) proposed to address such a situation. Meanwhile, they also considered the covariate shift in their paper. In the cross domain learning to rank problem, we carefully sample training data to avoid the class imbalance between source and target domain. Then, we adapt the method introduced in Jiang and Zhai (2007) to this new application scenario.

The common feature learning approach is widely studied in cross domain document classification. Dai et al. (2007) proposed to use transfer learning technique for mining text data across domains based on co-clustering. The learned knowledge is passed via common words. Here, single words are treated as features. Do and Ng (2006) considered to automatically meta-learn a parameter function which may then be applied to novel classification problems. The learned parameter function is thought to be shared knowledge across domains. Furthermore, in the multi-task setting, Ando and Zhang (2005) considered learning predictive structures on hypothesis spaces from multiple learning tasks. Their method works well in the semi-supervised learning setting. Argyriou et al. (2007) presented a method to learn a low-dimensional representation which is shared across multiple related tasks. In our problem setting, since we have labeled data from both source and target domain, we refer to Argyriou’s work and construct a learning problem to find common features which may then be effective for the ranking task in target domain.

3 Optimization for knowledge transfer in learning to rank

In our previous work (Chen et al. 2008), a pilot method was proposed to conduct knowledge transfer in learning to rank for the first time. It includes two consecutive steps which deal with the source domain and target domain training data, respectively, at instance level and feature level. However, further investigation on transfer learning as well as learning to rank shows that knowledge transfer at these two levels should be treated independently. In this section, we introduce two novel promising methods. Different from the heuristic method in (Chen et al. 2008), we solve the cross domain learning to rank problem from the machine learning perspective by formalizing it as optimization problems. A similar work by Wu et al. (2008) concerns the model adaptation problem in learning to rank. They aim to adapt an existing ranking model to various tasks. Differently, we simultaneously use the source and target training data in an integrated learning process.

3.1 Feature level knowledge transfer

In learning to rank, a set of features (e.g., document length, tf, idf, etc.) forms the hyperspace based on which the ranking model is learned. For different datasets, the data distribution varies much. However, during our data analysis, we find that certain features are shared between different datasets. For example, the tfidf feature performs well to rank the documents in both the OHSUMED and WSJ datasets.

In the cross domain learning to rank problem, since learning based only on the small amount of target domain training data D t results in an unreliable ranking model in the target domain, we resort to plentiful source domain data D s . In particular, we use these imprecise data to strengthen the subset of features which is inherently shared between D s and D t . An improved ranking model can then be obtained based on these shared features for the target domain. During the transfer learning survey, we find that we have a similar assumption with the NIPS work (Argyriou et al. 2007). In this subsection, we tailor their work to the learning to rank settings. Furthermore, we prove that the optimization in their method can be converted and solved by Ranking SVM.

3.1.1 Underlying assumption

The underlying assumption of feature-level knowledge transfer is that there exists a low-dimensional feature representation shared by both source and target domain data. For simplicity, we assume these common features to be the linear combinations of the original features,

$$ h_{i} \left( {\boldsymbol {x}} \right) = \left\langle {{\boldsymbol{u}}_{i} ,{\boldsymbol {x}}} \right\rangle $$
(8)

where x is the original feature vector and u i is the regression parameters for the new feature h i . We further assume that the vectors u i are orthonormal. Since x is a d dimensional vector, we use U to denote the d × d matrix with columns the vectors as u i . Obviously, the matrix U is an orthogonal matrix.

In this meaning, the cross domain learning to rank is a special case of multi-task learning (Caruana 1997), more precisely, a two-task learning problem. Multi-task learning has been empirically and theoretically shown to improve learning performance compared to learning each task independently. In this cross domain learning to rank scenario, we aim to learn these common features h i (x), i = 1, 2,… to help the learning of ranking model in target domain.

3.1.2 Optimization formulation

As many previous learning to rank algorithms did, we assume the ranking model f to be linear, that is \( f({\boldsymbol {h}})\,=\,\left \langle {{\boldsymbol {a}},{\boldsymbol{h}}} \right\rangle = {\boldsymbol {a}}^{T} {\boldsymbol {h}} \), where h is the learned common features. As a result, we have \( f({\boldsymbol {h}}) = {\boldsymbol {a}}^{T} {\boldsymbol {Ux}} =\left\langle {{\boldsymbol {w}},{\boldsymbol {x}}} \right\rangle \), where w = aU T. Let A = [a s , a t ] and W = [w s , w t ], where s and t stand for source domain and target domain, respectively, we have W = UA. Intuitively, according to the assumption that the source domain and target domain share a few common features, A should have some rows which are identically equal to zero.

In order to obtain such A and U via a learning process simultaneously, we utilize the (2, 1)-norm as the regularizer. This norm is obtained by first computing the l 2 norm of the rows of a matrix and forming a new vector, and then computing the l 1 norm of this new vector. Formally,

$$\left\| {\boldsymbol {M}} \right\|_{2,1}\,=\,\left\| {\left( {\left\|{m^{1} } \right\|_{2} ,\left\| {m^{2} } \right\|_{2} , \ldots,\left\| {m^{r} } \right\|_{2} } \right)} \right\|_{1} =\sum\limits_{i = 1, \ldots ,r} {\left\| {m^{i} } \right\|_{2} } $$
(9)

where m 1 represents the first row of M, m 2 stands for the second and so on. r is the number of rows of M. Then, the source and target domain ranking tasks can be combined to learn the common features by minimizing \(\left\| {\boldsymbol {A}} \right\|_{2,1}^{2} \). Using the pair-wise loss function in Eq. 4, the cross domain learning to rank problem can be formulated as,

$$\left( {{\boldsymbol {A}},{\boldsymbol {U}}} \right) = \arg\min_{{\boldsymbol {A}},{\boldsymbol {U}}} \sum\limits_{{k \in\left\{ {s,t} \right\}}} {\sum\limits_{i = 1}^{{N_{k} }} {l_{h}\left( {{\boldsymbol {a}}_{k} ;{\boldsymbol {U}}^{T} {\boldsymbol{y}}_{ki} ,z_{ki} } \right) + \gamma \left\| {\boldsymbol {A}}\right\|_{2,1}^{2} } }$$
(10)

where s indicates the source domain and t indicates the target domain; a k is the ranking model learned on the new feature representation; γ denotes the tradeoff between the training error and the (2, 1)-norm of matrix A. Clearly, this optimization problem is non-convex and we cannot optimize A and U simultaneously.

In their paper, Argyriou et al. (2007) proved that the above optimization problem can be solved by solving an equivalent convex optimization problem as follows,

$$ \begin{gathered} \left( {{\boldsymbol {W}},{\boldsymbol {D}}} \right) = \arg \min_{{\boldsymbol {W}},{\boldsymbol {D}}} \sum\limits_{{k \in \left\{ {s,t} \right\}}} {\sum\limits_{i = 1}^{{N_{k} }} {l_{h} \left( {{\boldsymbol {w}}_{k} ;{\boldsymbol {y}}_{ki} ,z_{ki} } \right) + \gamma } } \sum\limits_{{k \in \left\{ {s,t} \right\}}} {\left\langle {{\boldsymbol {w}}_{k} ,{\boldsymbol {D}}^{ + } {\boldsymbol {w}}_{k} } \right\rangle } \hfill \\ {\text{s}} . {\text{t}} .\;{\boldsymbol {W}} = {\boldsymbol {UA}},\;{\boldsymbol {D}} = {\boldsymbol {U}}{\text{Diag}}\left( {{\frac{{\left\| {{\boldsymbol {a}}^{i} } \right\|_{2} }}{{\left\| {\boldsymbol {A}} \right\|_{2,1} }}}} \right){\boldsymbol {U}}^{T} \in {\boldsymbol {S}}_{ + }^{d} ,\;{\text{trace}}\left( {\boldsymbol {D}} \right) \le 1, \hfill \\ {\text{range}}\left( {\boldsymbol {W}} \right) \subseteq {\text{range}}\left( {\boldsymbol {D}} \right) \hfill \\ \end{gathered} $$
(11)

where S d+ stands for the set of symmetric positive semi-definite matrices; a i denotes the i-th row of A; D + is the pseudo-inverse of matrix D. For more details of the proof, please refer to (Argyriou et al. 2007). The algorithm solving optimization in Eq. 11 is shown in Fig. 1. This algorithm is similar to the one proposed in (Argyriou et al. 2007), but tailored to the learning to rank problem. Moreover, the column w t of the output W is the desired ranking model on the original feature vector for the target domain, which is used to predict the unseen test data.

Fig. 1
figure 1

The optimization of Eq. (11)

Full size image

3.1.3 Learning with ranking SVM

The core part of the optimization in Fig. 1 is line 7. As we see, there are additional constraints on the target variable w. Also note that the regularizer \( \gamma \left\langle {{\boldsymbol {w}},{\boldsymbol {D}}^{ + }{\boldsymbol {w}}} \right\rangle \) is somewhat like the one of Ranking SVM (Herbrich et al. 2000), which is \( \lambda \left\| {\boldsymbol {w}} \right\|^{2} = \lambda\left\langle {{\boldsymbol {w}},{\boldsymbol {w}}} \right\rangle \). In the following theorem, we prove that this optimization problem can be effectively solved using Ranking SVM after certain conversion on the training data. Please refer to Eq. 7.

Theorem 4.1

The optimization in line 7 is equivalent to the following optimization problem:

$$ {\boldsymbol {w}} = {\boldsymbol {P}}^{T} \Upsigma^{{{\frac{1}{2}}}}\left[ {\arg \min_{{{\boldsymbol {u}}}} \left( {\sum\limits_{i =1}^{N} {l_{h} \left( {{\boldsymbol {u}};\Upsigma^{{{\frac{1}{2}}}}{\boldsymbol {Py}}_{i} ,z_{i} } \right) + \gamma \left\langle{{\boldsymbol {u}},{\boldsymbol {u}}} \right\rangle } } \right)}\right]$$
(12)

whereP and Σ are the right singular-vector and diagonal singular-value matrices in the singular-value decomposition (SVD) form of D, particularly D = PTΣP. Because \({\boldsymbol {D}} \in {\boldsymbol {S}}_{ + }^{d} \) is a symmetric positive semi-definite matrix, the left and right matrices after SVD are the transpose of each other.

Proof

Since \({\boldsymbol {w}} \in {\text{range}}({\boldsymbol {D}}) = \left\{{{\boldsymbol {w}} \in {\boldsymbol {R}}^{d} :{\boldsymbol {w}} ={\boldsymbol {Dv}} {\text{ for }} {\text{some }} {\boldsymbol {v}}\in {\boldsymbol {R}}^{d} } \right\}, \) plugging w = Dv into line 7 of Fig. 1, we can get

$$ {\boldsymbol {v}} = \arg \min_{{\boldsymbol {v}}} \left\{{\sum\limits_{i = 1}^{N} {l_{h} \left( {{\boldsymbol{Dv}}; {\boldsymbol {y}}_{i} ,z_{i} } \right) + \gamma \left\langle{{\boldsymbol {Dv}},{\boldsymbol {D}}^{ + } {\boldsymbol {Dv}}}\right \rangle :{\boldsymbol {v}} \in {\boldsymbol {R}}^{d} } }\right\}.$$
(13)

For the second item, \( \left\langle {{\boldsymbol {Dv}},{\boldsymbol {D}}^{ + }{\boldsymbol {Dv}}} \right\rangle = {\boldsymbol {v}}^{T}{\boldsymbol {D}}^{T} {\boldsymbol {D}}^{ + } {\boldsymbol {Dv}}. \)

Since D is symmetric, we have D T = D.

$$ \left\langle {{\boldsymbol {Dv}},{\boldsymbol {D}}^{ + }{\boldsymbol {Dv}}} \right\rangle = {\boldsymbol {v}}^{T}{\boldsymbol DD}^{ + } {\boldsymbol {Dv}} = {\boldsymbol v}^{T}{\boldsymbol {Dv}}$$

Conduct SVD on D, D = P TΣP,

$$\left\langle {\boldsymbol {Dv}},{\boldsymbol {D}}^{ + } {\boldsymbol{Dv}} \right\rangle = {\boldsymbol {v}}^{T} {\boldsymbol {P}}^{T}\Upsigma {\boldsymbol {Pv}}$$

Let u = Σ½ Pv,

$$ \left\langle {{\boldsymbol {Dv}},{\boldsymbol D}^{ + } {\boldsymbol{Dv}}} \right\rangle = {\boldsymbol {v}}^{T} {\boldsymbol {P}}^{T}\Upsigma^{{{\frac{1}{2}}}} \Upsigma^{{{\frac{1}{2}}}} {\boldsymbol Pv} =\left( {\Upsigma^{{{\frac{1}{2}}}} {\boldsymbol Pv}} \right)^{T}\Upsigma^{{{\frac{1}{2}}}} {\boldsymbol Pv} = {\boldsymbol {u}}^{T}{\boldsymbol {u}}. $$

Now, the second term of Eq. 13 becomes \(\gamma \left\| {\boldsymbol {u}} \right\|^{2}. \) Look at the first term, that is, the hinge loss.

$$ \begin{aligned} l_{h} \left( {{\boldsymbol {Dv}};{\boldsymbol {y}}_{i} ,z_{i} } \right) = 1 - z_{i} \left\langle {{\boldsymbol {Dv}},{\boldsymbol {y}}_{i} } \right\rangle = 1 - z_{i} \left( {\boldsymbol {Dv}} \right)^{T} {\boldsymbol {y}}_{i} \\ = 1 - z_{i} \left( {\boldsymbol {P}}^{T} \Upsigma {\boldsymbol {Pv}} \right)^{T} {\boldsymbol {y}}_{i} = 1 - z_{i} \left( {{\boldsymbol {P}}^{T} \Upsigma^{{{\frac{1}{2}}}} {\boldsymbol {u}}} \right)^{T} {\boldsymbol {y}}_{i} \\ = 1 - z_{i} {\boldsymbol {u}}^{T} \Upsigma^{{{\frac{1}{2}}}} {\boldsymbol {Py}}_{i} = 1 - z_{i} \left\langle {{\boldsymbol {u}},\Upsigma^{{{\frac{1}{2}}}} {\boldsymbol {Py}}_{i} } \right\rangle \\ = l_{h} \left( {{\boldsymbol {u}};\Upsigma^{{{\frac{1}{2}}}} {\boldsymbol {Py}}_{i} ,z_{i} } \right) \\ \end{aligned}$$

Therefore, we have the following optimization problem,

$$ {\boldsymbol {u}} = \arg \min_{{\boldsymbol {u}}} \left\{{\sum\limits_{i = 1}^{N} {l_{h} \left( {{\boldsymbol{u}};\Upsigma^{{{\frac{1}{2}}}} {\boldsymbol {Py}}_{i} ,z_{i} }\right) + \gamma \left\| {\boldsymbol {u}} \right\|^{2}:{\boldsymbol {u}} \in {\boldsymbol {R}}^{d} } } \right\}$$
(14)

We can see it is a standard optimization of Ranking SVM after we multiply each training vector y i with Σ½ P. After obtaining u, the w can be computed as

$$ {\boldsymbol {w}} = {\boldsymbol {Dv}} = {\boldsymbol {DP}}^{ - 1}{\Upsigma^{ - 1}} {\boldsymbol {u}} = {\boldsymbol {P}}^{T} \Upsigma{\boldsymbol {PP}}^{ - 1} \left( {\Upsigma^{{{\frac{1}{2}}}} } \right)^{ -1} {\boldsymbol {u}} = {\boldsymbol {P}}^{T} \Upsigma^{{{\frac{1}{2}}}}u$$
(15)

Combining Eqs. 14 and 15, this ends the proof of Theorem 4.1. □

We use CLRankfeat to denote the cross domain learning to rank at feature level and summarize it in Fig. 2. For the stop condition mentioned, we can set a threshold on the minimum change of D or simply stop the loop after a preset number of iterations.

Fig. 2
figure 2

The CLRankfeat algorithm

Full size image

3.2 Instance level knowledge transfer

3.2.1 Underlying assumption

Besides the feature level knowledge transfer, we further examine a more direct way to make use of the source domain data. The underlying assumption of instance level knowledge transfer is similar to domain adaptation, that is, since the source and target training data come from different but related distributions, we can adapt each source domain training example to the target domain from a probabilistic distribution’s view. Technically, this is implemented via instance weighting (Jiang and Zhai 2007). In detail, we analyze the distribution difference in two aspects and carry out the adaptation, respectively. Formally, one aspect concerns the difference between \( P_{s} \left( {z_{i} \left| {{\boldsymbol {y}}_{i} } \right.} \right) \) and \( P_{t} \left( {z_{i} \left| {{\boldsymbol {y}}_{i} } \right.} \right) \), while the other deals with the difference between P s (y i ) and P t (y i ).

3.2.2 Optimization formulation

According to the basic assumption introduced above, we aim to make full use of the data from both source and target domain. Using D t in the standard supervised learning way, we have

$${\boldsymbol {w}}_{t} = \arg \min_{{\boldsymbol {w}}} \sum\limits_{i= 1}^{{N_{t} }} {l_{h} \left( {{\boldsymbol {w}};{\boldsymbol{y}}_{ti} ,z_{ti} } \right)} $$
(16)

Again, l h is the pair-wise loss function for the learning to rank problem. In this way, we use the empirical risk to estimate the theoretical risk in the target domain. As aforementioned, N t is with a small scale, and hence it may cause the estimation inaccurate.

On the other hand, we can also utilize the labeled data from the source domain. Different from the way of using target domain data, these data cannot be used directly, since they are drawn from a distribution different from the one for future test data. In other words, we cannot use the empirical risk of these data to approximate the theoretical risk. We denote the source and target distributions by P s and P t , respectively.

$$ \begin{aligned} {\boldsymbol {w}}_{t} = \arg \min_{\boldsymbol {w}} \int\limits_{{{\boldsymbol {X}}^{2} \times {\boldsymbol {Z}}}} {l_{h} \left( {{\boldsymbol {w}};{\boldsymbol {y}},z} \right)P_{t} \left( {{\boldsymbol {y}},z} \right)\,{\text{d}}{\boldsymbol {y}}{\text{d}}z} \\ = \arg \min_{{\boldsymbol {w}}} \int\limits_{{{\boldsymbol {X}}^{2} \times {\boldsymbol {Z}}}} {{\frac{{P_{t} \left( {{\boldsymbol {y}},z} \right)}}{{P_{s} \left( {{\boldsymbol {y}},z} \right)}}}l_{h} \left( {{\boldsymbol {w}};{\boldsymbol {y}},z} \right)P_{s} \left( {{\boldsymbol {y}},z} \right)\,{\text{d}}{\boldsymbol {y}}{\text{d}}z} \\ = \arg \min_{{\boldsymbol {w}}} \int\limits_{{{\boldsymbol {X}}^{2} \times Z}} {{\frac{{P_{t} \left( {z|{\boldsymbol {y}}} \right)}}{{P_{s} \left( {z|{\boldsymbol {y}}} \right)}}}{\frac{{P_{t} \left( {\boldsymbol {y}} \right)}}{{P_{s} \left( {\boldsymbol {y}} \right)}}}l_{h} \left( {{\boldsymbol {w}};{\boldsymbol {y}},z} \right)P_{s} \left( {{\boldsymbol {y}},z} \right)\,{\text{d}}{\boldsymbol {y}}{\text{d}}z} \\ \end{aligned} $$

Let \(\delta = {{P_{t} (z\left| {\boldsymbol {y}} \right.)}/{{P_{s}(z\left| {\boldsymbol {y}} \right.)}}} \) and η = P t (y)/P s (y), we have

$${\boldsymbol {w}}_{t} = \arg \min_{{\boldsymbol {w}}}\int\limits_{{{\boldsymbol {X}}^{2} \times {\boldsymbol {Z}}}}{\delta \eta l_{h} \left( {{\boldsymbol {w}};{\boldsymbol {y}},z}\right)P_{s} \left( {{\boldsymbol {y}},z}\right)\,{\text{d}}{\boldsymbol {y}}{\text{d}}z} $$
(17)

If δ and η could be computed preliminarily, we can use D s to approximate the theoretical risk in the target domain,

$$ {\boldsymbol {w}}_{t} \approx \arg \min_{{\boldsymbol {w}}}\sum\limits_{i = 1}^{{N_{s} }} {\delta_{i} \eta_{i} l_{h} \left({{\boldsymbol {w}};{\boldsymbol {y}}_{si} ,z_{si} } \right)}$$
(18)

where \( \delta_{i} = {{P_{t} (z_{i} \left| {{\boldsymbol {y}}_{i} }\right.)}/{{P_{s} (z_{i} \left| {{\boldsymbol {y}}_{i} }\right.)}}}\) and η i  = P t (y i )/P s (y i ). Next, we will design a method to estimate these values, since they are critical in adjusting the source domain data to the target domain.

3.2.3 Learning with Ranking SVM

When using both D t and D s for training, we combine Eqs. 16 and 18. Therefore, the cross domain learning to rank at instance level, denoted by CLRankins, is expressed as follows. The last term is the Euclidean norm used to regularize the model complexity.

$$ {\boldsymbol {w}}_{t} = \arg \min_{{\boldsymbol {w}}} \left[{\sum\limits_{i = 1}^{{N_{s} }} {\delta_{i} \eta_{i} l_{h} \left({{\boldsymbol {w}};{\boldsymbol {y}}_{si} ,z_{si} } \right)} +\sum\limits_{i = 1}^{{N_{t} }} {l_{h} \left( {{\boldsymbol{w}};{\boldsymbol {y}}_{ti} ,z_{ti} } \right) + \lambda \left\|{\boldsymbol {w}} \right\|^{2} } } \right] $$

or

$${\boldsymbol {w}}_{t} = \arg \min_{{\boldsymbol {w}}} \sum\limits_{i= 1}^{{N_{s} + N_{t} }} {\psi_{i} l_{h} \left( {{\boldsymbol{w}};{\boldsymbol {y}}_{i} ,z_{i} } \right) + \lambda \left\|{\boldsymbol {w}} \right\|^{2} } $$
(19)

where \( \psi_{i} = \left\{ {\begin{array}{*{20}c} {1, \,\,{\text{for}}\;{\text{target}}\;{\text{domain}}\;{\text{data}}} \\ {\delta_{i} \eta_{i} ,\,{\text{for}}\;{\text{source}}\;{\text{domain}}\;{\text{data}}} \\ \end{array} } \right. \)

Equation 19 can be solved effectively using Ranking SVM directly. Note that, in this case, the training examples are associated with different weights. We employ some heuristic methods to compute the weight for each training example. Intuitively, if \( P_{t} (z_{i} \left| {{\boldsymbol {y}}_{i} } \right.) \) differs greatly from \( P_{s} (z_{i} \left| {{\boldsymbol {y}}_{i} } \right.) \), it should be discarded. To set δ i , we use the following heuristic method. We first train a ranking model from D t and then test it on D s . If a pair of documents in D s is ranked correctly, i.e., the corresponding y i is classified correctly, then the corresponding (y i , z i ) is retained and assigned with a weight; else, it is discarded. Since in learning to rank, each y i is associated with a specific query, we use the pairwise precision of this query as δ i . Formally,

$$ \delta_{i} = \left\{ \begin{gathered} {\frac{{\# {\text{pairs correctly ranked of a query}}}}{{\# {\text{total pairs of a query}}}}},{\text{ pair is correctly ranked}} \hfill \\ \, 0 \, ,{\text{ pair is wrongly ranked}} \hfill \\ \end{gathered} \right. $$

Accurately setting η i involves accurately estimating P s (y i ) and P t (y i ) from the empirical distribution. Due to the feature diversity in learning to rank and the absence of parametric model for P s (y i ) and P t (y i ), it is difficult to set η i . Since the estimation of η i is an independent problem from learning to rank, in this work, we will not explore further in this direction and simply set η i  = 1 for all the source domain training examples. We will study this problem in our future work.

4 Experiments

In this section, we systematically evaluate the effectiveness of the proposed knowledge transfer algorithms using three benchmark datasets. Sections 4.1–4.3 give the detailed experimental settings. Section 4.4 presents the main experimental results. Finally, Sect. 4.5 holds a discussion about our findings.

4.1 Datasets

Three benchmark datasets are used in our experiments: LETOR 3.0 (Liu et al. 2007), WSJ and AP. The latter two are datasets from the TREC ad-hoc retrieval track. The former one is a recently published benchmark dataset for learning to rank, including the .gov data from TREC 2003 and 2004 web track, and the OHSUMED data which is a subset of MEDLINE.Footnote 3

Since there are no ready datasets suitable for cross domain learning to rank problem, we manually construct several cross domain learning to rank scenarios using the above three datasets. There are three search tasks in the LETOR .gov dataset, namely, topic distillation (td), homepage finding (hp) and named page finding (np). We perform cross domain learning to rank on each task by using TREC 2003 data as the source domain and TREC 2004 data as the target domain. It is a natural instance of using outdated data.

We further construct more cases using the OHSUMED (the LETOR version), WSJ and AP datasets. Since they come from different publication source, we treat them as data from different domains in order to simulate the scenario where out-of-domain data are used. The WSJ and AP datasets are not included in LETOR, so we need to manually extract features as same as those defined for OHSUMED in LETOR. WSJ contains 74,520 news articles from Wall Street Journal from 1990 to 1992, and AP contains 158,240 news articles from Associate Press in 1988 and 1990. We selected No. 101–No. 300 TREC topics. Each topic (i.e., query) is associated with a number of documents, labeled “relevant” or “irrelevant”. Following the previous work (Trotman 2005), we dropped the queries that have less than ten relevant documents. During feature extraction, for WSJ, we use its <HL> field as “title”, while <TEXT> as “abstract” (<LP> is also added). For AP, the “title” is the <HEAD> field and the “abstract” <TEXT>. Moreover, to ensure that each query has nearly equal number of documents with the queries in OHSUMED, we randomly sampled 150 documents for each query in WSJ and AP.

We summarize the usage of datasets in Table 1, where the symbol T denotes the test data from the target domain.

Table 1 The usage of datasets for cross domain learning to rank
Full size table

4.2 Evaluation measures

To evaluate the performance of the learned ranking model, we use normalized discounted cumulative gain (NDCG) and mean average precision (MAP) as measures. They are both widely used in the literature of learning to rank. NDCG is the abbreviation of Normalized Discounted Cumulative Gain. NDCG@n is calculated as

$$ {\text{NDCG}}@n = Z_{n} \sum\limits_{j = 1}^{n} {{\frac{{2^{R\left( j \right)} - 1}}{{\log \left( {1 + j} \right)}}}} $$

where R(j) is the relevance level of j-th document in the ranking list. Z n is a normalization factor that guarantees the ideal NDCG@n equals to 1. MAP is the abbreviation of Mean Average Precision. First, the precision at position n is defined as

$$ P\left( n \right) = {\frac{{\# {\text{ relevant instances in top }}n}}{n}} $$

Then, the average precision of a ranking list is calculated based on P(n).

$$ {\text{AP}} = \sum\limits_{n = 1}^{N} {{\frac{P\left( n \right) \times pos\left( n \right)}{{\# {\text{relevant instances}}}}}} $$

where N is the total number of ranked documents. pos(n) is a binary function, valued 1 when the document at position n is relevant. Finally, MAP is defined as the AP value averaged over all queries. It is worth mentioning that since the OHSUMED dataset has three relevance levels, we will treat “partially relevant” as irrelevant when calculating MAP.

4.3 Baselines

Since no related work previously proposed, three baseline algorithms are implemented to be compared with our knowledge transfer algorithms. Table 2 gives their descriptions.

Table 2 The description of baseline methods
Full size table

LRankstd denotes the standard learning to rank using D t , but omitting D s . In LRankmix, we mix D s and D t directly, and use them as training data to obtain a ranking model. LRankmix_w is an improved version of LRankmix. In this method, we weigh the source domain data through tuning on a target domain validation set. All the training examples in source domain will be given a same weight after tuning, and then mixed with the target domain data. All the baseline algorithms above utilize Ranking SVM as the basic learner, with the default parameter setting. For the Ranking SVM tool, we use SVMlight. Besides, we represent the proposed knowledge transfer algorithms as CLRankfeat and CLRankins, respectively.

4.4 Experimental results

A single round of our experiments consists of the following steps:

  1. 1.

    Randomly split the target domain data into two parts: the target domain training set D t and the final test set T.

  2. 2.

    Run the three baseline methods and two knowledge transfer methods using D s and D t .

  3. 3.

    Test the obtained ranking models using T.

Table 3 lists the performance comparison among all the methods when the ratio between target and source domain training data is 0.1. All these values are MAP value averaged over ten random rounds. The γ in CLRankfeat is tuned to be 100 using a validation set. In our experiments, we find that CLRankfeat converges quickly, generally within ten iterations, which indicates that CLRankfeat can find a solution with acceptable computational cost.

Table 3 Comparison on MAP values (ratio = 0.1, 5–15 queries in target domain)
Full size table

From Table 3, we can see that CLRankfeat consistently produces the best performance except for Group 4. The percentage in the bracket denotes the relative improvements over LRankstd. There are large improvements brought by CLRankfeat. All the improvements by CLRankfeat have been verified to be statistically significant (p-value <0.05) through t test. This means that the knowledge has been successfully transferred from source domain to target domain and helps obtain a more accurate ranking model. Besides, CLRankins does work well in some groups while fails in others. This failure phenomenon is known as negative transfer (Rückert 2008). We will discuss the possible causes in Sect. 4.5. An interesting observation in Table 3 is that LRankmix always lowers the performance of LRankstd. In other words, directly using the source domain data does not improve but hurt the performance. It is probably because the data with different distributions confuse and conflict with each other, hence making the learned model unstable. The improved LRankmix_w performs better than other two baselines as expected. For Group 1, 2, 3 and 5 where CLRankins fails, this simple weighting method keeps getting steady improvements over the other baselines. As in information retrieval, the top-ranked results are much more concerned, we futher give the NDCG@5 values in Table 4. The results are consistent with those in Table 3.

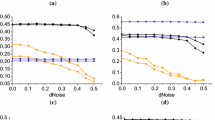
Table 4 Comparison on NDCG@5 values (ratio = 0.1, 5–15 queries in target domain)
Full size table

We also do experiments to investigate the effect of ratio between target and source domain training data. Figure 3 focuses on Group 1 (source: AP; target: OHSUMED). Similar results are also observed on other groups. We generally increase the ratio from 0.05 to 0.5, by 0.05 each time. As shown in Fig. 3, CLRankfeat can consistently outperform the baseline methods in terms of MAP, while CLRankins fails as indicated in Tables 3 and 4. With the ratio getting larger, the improvement by CLRankfeat goes slighter. We believe that the source domain dataset D s contains not only useful knowledge, but also noisy data. When there are too few target training examples to train a good ranking model, the useful knowledge in the source domain data is dominant while the noisy data will not affect the learner too much. However, when the amount of target domain data gets larger, nearly enough to train a good ranking model by itself, the source domain data perform much like noisy data. In all, the main contribution of cross domain learning to rank is that it only needs a small amount of target domain labeled data to achieve comparative accuracy. By employing these methods, the tedious labeling work can be lightened.

Fig. 3
figure 3

Performance curves with different ratios

Full size image

Finally, we tune the parameter γ on the performance of CLRankfeat. We again focus on Group 1 with ratio set to 0.1, and change γ from 10−3 to 103. This experiment also runs ten random rounds. In Fig. 4, we draw the performance curves for LRankstd, LRankmix, LRankmix_w, and CLRankfeat. We can see that CLRankfeat reaches the peak when γ = 100. We also perform this experiment on other groups and get similar results. Therefore, in all our experiments, we fix γ to 100.

Fig. 4
figure 4

The effect of γ on the performance of CLRankfeat

Full size image

4.5 Discussions

From the above experiments, we can draw the following conclusions: CLRankfeat is an effective knowledge transfer method; CLRankins gains some improvements on the .gov dataset while impairs the performance on the WSJ, AP and OHSUMED. Here are some possible causes of our observations.

  1. 1.

    The estimation methods for δ i and η i may not be suitable, especially without a parametric model to accurately estimate η = P t (y)/P s (y).

  2. 2.

    Due to the heterogeneous features in learning to rank (features have quite different meanings), to inspect the instance relationship based on the whole feature vector involves too many unknown factors. It may cause the domain adaptation or the definition of instance similarity function uncertain.

  3. 3.

    CLRankins improves the ranking model on the .gov dataset, probably because the source and target domain data are drawn from the same document repository (a January, 2002 crawl of the .gov domain), in other words, their distributions do not differ too much.

5 Conclusions

Motivated by the labeled data shortage in real world learning to rank applications, in this paper, we address a challenging problem, which is defined as cross domain learning to rank. Starting from a heuristic method introduced in our previous work, we theoretically study the knowledge transfer for learning to rank at feature level and instance level, with two promising methods proposed, respectively. Both methods obtain the ranking model by solving an optimization problem using Ranking SVM as the basic learner. Experiments show that the feature-level knowledge transfer method can always gain improvements over baselines, while the instance-level method only works well for certain dataset groups. After further analysis, we draw the conclusion that feature-level knowledge transfer is more suitable for the learning to rank problem.

In our future work, we plan to further study the cross domain learning to rank problem under the scenario where the source and target domain data originally have different feature sets. We may also consider integrating the two methods into a single one bridged by Ranking SVM to seek potential improvement.