Skip to main content

Advertisement

Springer Nature Link
Log in

Eisbach: A Proof Method Language for Isabelle

  • Published:
Journal of Automated Reasoning Aims and scope Submit manuscript

Abstract

Machine-checked proofs are becoming ever-larger, presenting an increasing maintenance challenge. Isabelle’s most popular language interface, Isar, is attractive for new users, and powerful in the hands of experts, but has previously lacked a means to write automated proof procedures. This can lead to undesirable duplication in large proofs. In this paper we present Eisbach, a proof method language for Isabelle, which aims to fill this gap by incorporating Isar language elements, thus making it accessible to end-users. We describe the language and the design principles on which it was developed. We evaluate its effectiveness by implementing the most-widely used proof tools in the seL4 verification stack, and consider its strengths and limitations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Notes

  1. https://github.com/seL4/l4v.

  2. http://afp.sf.net.

  3. This distinction should not be confused with that between structured and unstructured proofs: structured proofs usually contain at most one structured method invocation (the final one); unstructured proofs contain few (if any) unstructured method invocations.

  4. This is why we need to use the

    figure iv

    combinator in this example and the

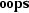
    figure iw

    keyword to terminate an unfinished proof.

  5. See also [2] for a recent exposition of the possibilities of locales and locale interpretations via morphisms in Isabelle.

  6. See https://github.com/NICTA/l4v/tree/master/proof/invariant-abstract.

References

  1. Ballarin, C.: Locales and locale expressions in Isabelle/Isar. In: Berardi, S., Coppo, M., Damiani, F. (eds.) Types for Proofs and Programs (TYPES 2003). Lecture Notes in Computer Science, vol. 3085. Springer (2003). doi:10.1007/978-3-540-24849-1_3

  2. Ballarin, C.: Locales: a module system for mathematical theories. J. Autom. Reason. 52(2), 123–153 (2014). doi:10.1007/s10817-013-9284-7

    Article  MathSciNet  MATH  Google Scholar 

  3. Bourke, T., Daum, M., Klein, G., Kolanski, R.: Challenges and experiences in managing large-scale proofs. In: Wenzel, M. (ed.) Conferences on Intelligent Computer Mathematics (CICM)/Mathematical Knowledge Management. Springer (2012). doi:10.1007/978-3-642-31374-5_3

  4. Chlipala, A.: Mostly-automated verification of low-level programs in computational separation logic. ACM SIGPLAN Not. 46(6), 234 (2011). doi:10.1145/1993316.1993526

    Article  Google Scholar 

  5. Cock, D., Klein, G., Sewell, T.: Secure microkernels, state monads and scalable refinement. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) 21st TPHOLs, LNCS, vol. 5170, pp. 167–182. Springer, Montreal, Canada (2008). doi:10.1007/978-3-540-71067-7_16

  6. Delahaye, D.: A tactic language for the system Coq. In: International Conference on Logic for Programming and Artificial Intelligence & Reasoning, LNCS, vol. 1955. Springer (2000). doi:10.1007/3-540-44404-1_7

  7. Gonthier, G., Mahboubi, A.: An introduction to small scale reflection in Coq. J. Formaliz. Reason. (2010). doi:10.6092/issn.1972-5787/1979

  8. Gonthier, G., Ziliani, B., Nanevski, A., Dreyer, D.: How to make ad hoc proof automation less ad hoc. J. Funct. Program. 23(4), 357–401 (2013). doi:10.1017/S0956796813000051

    Article  MathSciNet  MATH  Google Scholar 

  9. Gordon, M.J.C., Milner, R., Wadsworth, C.P.: Edinburgh LCF: A Mechanized Logic of Computation. LNCS 78. Springer (1979). doi:10.1007/3-540-09724-4

  10. Hölzl, J., Lochbihler, A., Traytel, D.: A formalized hierarchy of probabilistic system types. In: Urban, C., Zhang, X. (eds.) Interactive Theorem Proving. Lecture Notes in Computer Science, vol. 9236, pp. 203–220. Springer International Publishing (2015). doi:10.1007/978-3-319-22102-1_13

  11. Klein, G., Andronick, J., Elphinstone, K., Murray, T., Sewell, T., Kolanski, R., Heiser, G.: Comprehensive formal verification of an OS microkernel. ACM Trans. Comput. Syst. (TOCS) 32(1), 2 (2014). doi:10.1145/2560537

    Article  Google Scholar 

  12. Klein, G., Elphinstone, K., Heiser, G., Andronick, J., Cock, D., Derrin, P., Elkaduwe, D., Engelhardt, K., Kolanski, R., Norrish, M., Sewell, T., Tuch, H., Winwood, S.: seL4: formal verification of an OS kernel. In: SOSP, pp. 207–220. ACM, Big Sky, MT, USA (2009). doi:10.1145/1629575.1629596

  13. Matichuk, D., Wenzel, M., Murray, T.: An Isabelle proof method language. In: Klein, G., Gamboa, R. (eds.) Interactive Theorem Proving—-5th International Conference, ITP 2014, Vienna, Austria. Lecture Notes in Computer Science, vol. 8558. Springer (2014). doi:10.1007/978-3-319-08970-6_25

  14. Murray, T., Matichuk, D., Brassil, M., Gammie, P., Klein, G.: Noninterference for operating system kernels. In: Hawblitzel, C., Miller, D. (eds.) The Second International Conference on Certified Programs and Proofs, pp. 126–142. Springer, Kyoto (2012). doi:10.1007/978-3-642-35308-6_12

  15. Nipkow, T., Paulson, L., Wenzel, M.: Isabelle/HOL—-A Proof Assistant for Higher-Order Logic. Lecture Notes in Computer Science, vol. 2283. Springer Verlag (2002). doi:10.1007/3-540-45949-9

  16. Paulson, L.C.: Isabelle: the next 700 theorem provers. In: Odifreddi, P. (ed.) Logic and Computer Science. Academic Press (1990)

  17. Wenzel, M.: Isabelle/Isar—a versatile environment for human-readable formal proof documents. Ph.D. thesis, Technische Universität München (2002)

  18. Wenzel, M., Chaieb, A.: SML with antiquotations embedded into Isabelle/Isar. In: Carette, J., Wiedijk, F. (eds.) Workshop on Programming Languages for Mechanized Mathematics (PLMMS 2007). Hagenberg, Austria (2007)

  19. Wiedijk, F. (ed.): The Seventeen Provers of the World, vol. 3600 (2006). doi:10.1007/11542384_1

  20. Ziliani, B., Dreyer, D., Krishnaswami, N.R., Nanevski, A., Vafeiadis, V.: Mtac: a monad for typed tactic programming in Coq. In: Morrisett, G., Uustalu, T. (eds.) ICFP. ACM (2013). doi:10.1017/S0956796813000051

Download references

Acknowledgments

We would like to thank Gerwin Klein, who was involved in the discussions on the design of Eisbach and who provided early feedback on this paper. Thanks also to Peter Gammie, Magnus Myreen, and Thomas Sewell for feedback on drafts of this paper. NICTA is funded by the Australian Government through the Department of Communications and the Australian Research Council through the ICT Centre of Excellence Program.

Author information

Authors and Affiliations

  1. NICTA, Sydney, Australia

    Daniel Matichuk & Toby Murray

  2. School of Computer Science and Engineering, UNSW, Sydney, Australia

    Daniel Matichuk & Toby Murray

Authors
  1. Daniel Matichuk
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Toby Murray
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Makarius Wenzel
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Daniel Matichuk.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Matichuk, D., Murray, T. & Wenzel, M. Eisbach: A Proof Method Language for Isabelle. J Autom Reasoning 56, 261–282 (2016). https://doi.org/10.1007/s10817-015-9360-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10817-015-9360-2

Keywords