Skip to main content
Springer Nature Link
Log in

Optimal Deterministic Controller Synthesis from Steady-State Distributions

  • Published:
Journal of Automated Reasoning Aims and scope Submit manuscript

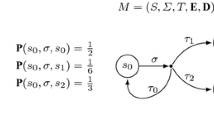
Abstract

The formal synthesis of control policies is a classic problem that entails the computation of optimal strategies for an agent interacting in some environment such that some formal guarantees of behavior are met. These guarantees are specified as part of the problem description and can be supplied by the end user in the form of various logics (e.g., Linear Temporal Logic and Computation Tree Logic) or imposed via constraints on agent-environment interactions. The latter has received significant attention in recent years within the context of constraints on the asymptotic frequency with which an agent visits states of interest. This is captured by the steady-state distribution of the agent. The formal synthesis of stochastic policies satisfying constraints on this distribution has been studied. However, the derivation of deterministic policies for the same has received little attention. In this paper, we focus on this deterministic steady-state control problem, i.e., the problem of obtaining a deterministic policy for optimal expected-reward behavior in the presence of linear constraints representing the desired steady-state behavior. Two integer linear programs are proposed and validated experimentally to solve this problem in unichain and multichain Markov decision processes. Finally, we prove that this problem is NP-hard even in the restricted setting where deterministic transitions are enforced on the MDP and there are only two actions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Akshay, S., Bertrand, N., Haddad, S., Helouet, L.: The steady-state control problem for Markov decision processes. In: International conference on quantitative evaluation of systems, pp 290–304. Springer (2013)

  2. Altman, E.: Constrained Markov Decision Processes, vol. 7. CRC Press, Boca Raton (1999)

    MATH  Google Scholar 

  3. Altman, E.: Constrained Markov Decision Processes, vol. 7. CRC Press, Boca Raton (1999)

    MATH  Google Scholar 

  4. Atia, G.K., Beckus, A., Alkhouri, I., Velasquez, A.: Steady-state policy synthesis in multichain Markov decision processes. In: Proceedings of the 29th international joint conference on artificial intelligence (IJCAI), pp 4069–4075. International joint conferences on artificial intelligence organization, 7 (2020)

  5. Atia, G.K., Beckus, A., Alkhouri, I., Velasquez, A.: Steady-state planning in expected reward multichain MDPS. J. Artif. Intell. Res. 72, 1029–1082 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  6. Baier, C., Haverkort, B, Hermanns, H., Katoen, J.-P.: Model checking continuous-time markov chains by transient analysis. In: International conference on computer aided verification, pp 358–372. Springer (2000)

  7. Baumgartner, P., Thiébaux, S., Trevizan, F.: Heuristic search planning with multi-objective probabilistic ltl constraints. In: Sixteenth international conference on principles of knowledge representation and reasoning (2018)

  8. Bhatnagar, S., Lakshmanan, K.: An online actor–critic algorithm with function approximation for constrained Markov decision processes. J. Optim. Theory Appl. 153(3), 688–708 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  9. Boussemart, M., Limnios, N.: Markov decision processes with asymptotic average failure rate constraint. Commun. Stat. Theory Methods 33(7), 1689–1714 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  10. Boussemart, M., Limnios, N., Fillion, J.C.: Non-ergodic Markov decision processes with a constraint on the asymptotic failure rate: general class of policies. Stoch. Models 18(1), 173–191 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  11. Brázdil, T., Brozek, V., Chatterjee, K., Forejt, V., Kucera, A.: Two views on multiple mean-payoff objectives in Markov decision processes. Log. Methods Comput. Sci. 10(1), 158 (2014)

    Article  MATH  Google Scholar 

  12. Brockman, G., Cheung, V., Pettersson, L., Schneider, J., Schulman, J., Tang, J., Zaremba, W.: Openai gym. (2016) arXiv preprint arXiv:1606.01540

  13. Camacho, A., McIlraith, S.A.: Strong fully observable non-deterministic planning with ltl and ltlf goals. In: Proceedings of the twenty-eighth international joint conference on artificial intelligence, IJCAI-19, pp 5523–5531. International joint conferences on artificial intelligence organization, 7 (2019)

  14. Chatterjee, K., Kretínsk, Z., Kretínský, J.: Unifying two views on multiple mean-payoff objectives in Markov decision processes. Log. Methods Comput. Sci. 113(2), 258 (2017)

    Google Scholar 

  15. Christos, H.: Papadimitriou: Computational Complexity. Addison-Wesley, New York (1994)

    Google Scholar 

  16. Courcoubetis, C., Yannakakis, M.: The complexity of probabilistic verification. J. ACM 42(4), 857–907 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  17. Dufour, F., Prieto-Rumeau, T.: Approximation of average cost Markov decision processes using empirical distributions and concentration inequalities. Stochast. Int. J. Probab. Stoch. Process. 87(2), 273–307 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  18. Engesser, T., Bolander, T., Nebel, B.: Cooperative epistemic multi-agent planning with implicit coordination. In: Distributed and multi-agent planning (DMAP-15), p 68

  19. Etessami, K., Kwiatkowska, M.Z., Vardi, M.Y., Yannakakis, M.: Multi-objective model checking of Markov decision processes. Log. Methods Comput. Sci. 4, 4 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  20. Guo, M., Zavlanos, M.M.: Probabilistic motion planning under temporal tasks and soft constraints. IEEE Trans. Autom. Control 63(12), 4051–4066 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  21. Ibm ilog cplex optimization studio v12.8.0 documentation. IBM Knowledge Center (2017)

  22. Kallenberg, L.C.M.: Linear Programming and Finite Markovian Control Problems. Mathematisch Centrum, Amsterdam (1983)

    MATH  Google Scholar 

  23. Kazemi, M., Perez, M., Somenzi, F., Soudjani, S., Trivedi, A., Velasquez, A.: Translating omega-regular specifications to average objectives for model-free reinforcement learning. In: Proceedings of the 21st international conference on autonomous agents and multiagent systems, pp 732–741 (2022)

  24. Konstantopoulos, T: Markov Chains and Random Walks. Lecture notes (2009)

  25. Koopman, P., Wagner, M.: Challenges in autonomous vehicle testing and validation. SAE Int. J. Transp. Saf. 4(1), 15–24 (2016)

    Article  Google Scholar 

  26. Krass, Dmitry, Vrieze, O.J.: Achieving target state-action frequencies in multichain average-reward Markov decision processes. Math. Oper. Res. 27(3), 545–566 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  27. Křetínskỳ, J.: Ltl-constrained steady-state policy synthesis. (2021) arXiv preprint arXiv:2105.14894

  28. Kwiatkowska, M., Parker, D.: Automated verification and strategy synthesis for probabilistic systems. In: Automated technology for verification and analysis, pp 5–22. Springer (2013)

  29. Lakshmanan, K., Bhatnagar, S.: A novel q-learning algorithm with function approximation for constrained Markov decision processes. In 2012 50th Annual Allerton Conference on Communication, Control, and Computing (Allerton), pp 400–405. IEEE (2012)

  30. Lazar, Andreas: Optimal flow control of a class of queueing networks in equilibrium. IEEE Trans. Automatic Control 28(11), 1001–1007 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  31. Medina Ayala, A.I., Andersson, S.B., Belta, C.: Probabilistic control from time-bounded temporal logic specifications in dynamic environments. In: 2012 IEEE international conference on robotics and automation, pp 4705–4710. IEEE (2012)

  32. Norris, J.R.: Markov Chains. Cambridge University Press, Cambridge (1997)

    Book  MATH  Google Scholar 

  33. Pak, Igor, Yang, Jed: Tiling simply connected regions with rectangles. J. Combinat. Theory Ser. A 120(7), 1804–1816 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  34. Pistore, M., Bettin, R., Traverso, P.: Symbolic techniques for planning with extended goals in non-deterministic domains. In: Sixth European conference on planning (2014)

  35. Puterman, Martin: Markov Decision Processes : Discrete Stochastic Dynamic Programming. Wiley, New York (1994)

    Book  MATH  Google Scholar 

  36. Saldi, N.: Finite-state approximations to discounted and average cost constrained Markov decision processes. IEEE Transactions on Automatic Control (2019)

  37. Sarathy, V., Kasenberg, D.l, Goel, S., Sinapov, J., Scheutz, M.: Spotter: extending symbolic planning operators through targeted reinforcement learning. In: Proceedings of the 20th International Conference on Autonomous Agents and MultiAgent Systems, pp 1118–1126 (2021)

  38. Schwarting, W., Alonso-Mor, J., Rus, D.: Planning and decision-making for autonomous vehicles. Robot. Autonom. Syst. Ann. Rev. Control 1, 187–210 (2018)

    Article  Google Scholar 

  39. Song, L., Feng, Y. Zhang, L.: Planning for stochastic games with co-safe objectives. In: Twenty-fourth international joint conference on artificial intelligence (2015)

  40. Sutton, R.S., Barto, A.G.: Reinforcement Learning: An Introduction, vol. 1. MIT Press, Cambridge (1998)

    MATH  Google Scholar 

  41. Teichteil-Königsbuch, F.: Path-constrained markov decision processes: bridging the gap between probabilistic model-checking and decision-theoretic planning. In: 20th European Conference on Artificial Intelligence (ECAI 2012) (2012)

  42. Thiébaux, S., Gretton, C., Slaney, J., Price, D., Kabanza, F.: Decision-theoretic planning with non-markovian rewards. J. Artif. Intell. Res. 25, 17–74 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  43. Trevizan, F.W, Thiébaux, S., Santana, P.H., Williams, B.C.: Heuristic search in dual space for constrained stochastic shortest path problems. In: ICAPS, pp 326–334 (2016)

  44. Velasquez, A.: Steady-state policy synthesis for verifiable control. In: Proceedings of the twenty-eighth international joint conference on artificial intelligence, IJCAI-19, pp. 5653–5661. International Joint Conferences on Artificial Intelligence Organization, 7 (2019)

  45. Wan, Y., Naik, A., Sutton, R.S.: Learning and planning in average-reward markov decision processes. In: International Conference on Machine Learning, pp 10653–10662. PMLR (2021)

Download references

Author information

Authors and Affiliations

  1. University of Colorado, Boulder, CO, USA

    Alvaro Velasquez

  2. University of Central Florida, Orlando, FL, USA

    Ismail Alkhouri & George Atia

  3. West Virginia University, Morgantown, WV, USA

    K. Subramani & Piotr Wojciechowski

Authors
  1. Alvaro Velasquez
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ismail Alkhouri
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. K. Subramani
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Piotr Wojciechowski
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. George Atia
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to K. Subramani.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This research was supported in part by the Air-Force Office of Scientific Research through Grant FA9550-19-1-0177 and in part by the Air-Force Research Laboratory, Rome through Contract FA8750-17-S-7007.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Velasquez, A., Alkhouri, I., Subramani, K. et al. Optimal Deterministic Controller Synthesis from Steady-State Distributions. J Autom Reasoning 67, 7 (2023). https://doi.org/10.1007/s10817-022-09657-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10817-022-09657-9

Keywords