Skip to main content

Advertisement

Springer Nature Link
Log in

A blind SAMPL6 challenge: insight into the octanol-water partition coefficients of drug-like molecules via a DFT approach

  • Published:
Journal of Computer-Aided Molecular Design Aims and scope Submit manuscript

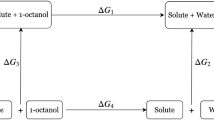
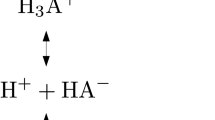Abstract

In this study quantum mechanical methods were used to predict the solvation energies of a series of drug-like molecules both in water and in octanol, in the context of the SAMPL6 n-octanol/water partition coefficient challenge. In pharmaceutical design, n-octanol/water partition coefficient, LogP, describes the drug’s hydrophobicity and membrane permeability, thus, a well-established theoretical method that rapidly determines the hydrophobicity of a drug, enables the progress of the drug design. In this study, the solvation free energies were obtained via six different methodologies (B3LYP, M06-2X and ωB97XD functionals with 6-311+G** and 6-31G* basis sets) by taking into account the environment implicitly; the methodology chosen (B3LYP/6-311+G**) was used later to evaluate ΔGsolv by using explicit water as solvent. We optimized each conformer in different solvents separately, our calculations have shown that the stability of the conformers is highly dependent on the solvent environment. We have compared implicitly and explicitly solvated systems, the interaction of one explicit water with drug-molecules at the proper location leads to the prediction of more accurate LogP values.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Leo A, Hansch C, Elkins D (1971) Partition coefficients and their uses. Chem Rev 71:525–616. https://doi.org/10.1021/cr60274a001

    Article  CAS  Google Scholar 

  2. Leo AJ (1993) Calculating log Poct from Structures. Chem Rev 93(4):1281–1306. https://doi.org/10.1021/cr00020a001

    Article  CAS  Google Scholar 

  3. Tehrany EA, Fournier F, Desobry S (2004) Simple method to calculate octanol-water partition coefficient of organic compounds. J Food Eng 64:315–320. https://doi.org/10.1016/j.jfoodeng.2003.10.015

    Article  Google Scholar 

  4. Sangster J (1997) Octanol-water partition coefficients: fundamentals and physical chemistry. Eur J Med Chem 32:842. https://doi.org/10.1016/s0223-5234(97)82764-x

    Article  Google Scholar 

  5. Kujawski J, Popielarska H, Myka A et al (2012) The log P parameter as a molecular descriptor in the computer-aided drug design – an overview. Comput Methods Sci Technol 18:81–88. https://doi.org/10.12921/cmst.2012.18.02.81-88

    Article  Google Scholar 

  6. Garrido NM, Jorge M, Queimada AJ et al (2011) Using molecular simulation to predict solute solvation and partition coefficients in solvents of different polarity. Phys Chem Chem Phys 13:9155–9164. https://doi.org/10.1039/c1cp20110g

    Article  CAS  PubMed  Google Scholar 

  7. Bannan CC, Calabró G, Kyu DY, Mobley DL (2016) Calculating partition coefficients of small molecules in octanol/water and cyclohexane/water. J Chem Theory Comput 12:4015–4024. https://doi.org/10.1021/acs.jctc.6b00449

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  8. Port A, Bordas M, Enrech R et al (2018) Critical comparison of shake-flask, potentiometric and chromatographic methods for lipophilicity evaluation (log Po/w) of neutral, acidic, basic, amphoteric, and zwitterionic drugs. Eur J Pharm Sci 122:331–340. https://doi.org/10.1016/j.ejps.2018.07.010

    Article  CAS  PubMed  Google Scholar 

  9. Xiang Q, Shan G, Wu W et al (2018) Measuring log Kow coefficients of neutral species of perfluoroalkyl carboxylic acids using reversed-phase high-performance liquid chromatography. Environ Pollut 242:1283–1290. https://doi.org/10.1016/J.ENVPOL.2018.08.009

    Article  CAS  PubMed  Google Scholar 

  10. Ogden PB, Dorsey JG (2019) Reversed phase HPLC with high temperature ethanol/water mobile phases as a green alternative method for the estimation of octanol/water partition coefficients. J Chromatogr A 1601:243–254. https://doi.org/10.1016/J.CHROMA.2019.05.002

    Article  CAS  PubMed  Google Scholar 

  11. Geballe MT, Skillman AG, Nicholls A et al (2010) The SAMPL2 blind prediction challenge: introduction and overview. J Comput Aided Mol Des 24:259–279

    Article  CAS  Google Scholar 

  12. Skillman AG (2012) SAMPL3: blinded prediction of host–guest binding affinities, hydration free energies, and trypsin inhibitors. J Comput Aided Mol Des 26:473–474. https://doi.org/10.1007/s10822-012-9580-z

    Article  CAS  PubMed  Google Scholar 

  13. Muddana HS, Daniel Varnado C, Bielawski CW et al (2012) Blind prediction of host–guest binding affinities: a new SAMPL3 challenge. J Comput Aided Mol Des 26:475–487. https://doi.org/10.1007/s10822-012-9554-1

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  14. Muddana HS, Fenley AT, Mobley DL, Gilson MK (2014) The SAMPL4 host-guest blind prediction challenge: an overview. J Comput Aided Mol Des 28:305–317. https://doi.org/10.1007/s10822-014-9735-1

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  15. Mobley DL, Wymer KL, Lim NM, Guthrie JP (2014) Blind prediction of solvation free energies from the SAMPL4 challenge. J Comput Aided Mol Des 28:135–150. https://doi.org/10.1007/s10822-014-9718-2

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  16. Wu SC, Tan CS, Huang MH (2017) Strong facet effects on interfacial charge transfer revealed through the examination of photocatalytic activities of various Cu2O–ZnO heterostructures. Adv Funct Mater 27(9):1604635. https://doi.org/10.1002/adfm.201604635

    Article  CAS  Google Scholar 

  17. Nicholls A, Mobley DL, Guthrie JP et al (2008) Predicting small-molecule solvation free energies: an informal blind test for computational chemistry. J Med Chem 51:769–779. https://doi.org/10.1021/jm070549+

    Article  CAS  PubMed  Google Scholar 

  18. Muddana HS, Gilson MK (2012) Prediction of SAMPL3 host-guest binding affinities: evaluating the accuracy of generalized force-fields. J Comput Aided Mol Des 26:517–525. https://doi.org/10.1007/s10822-012-9544-3

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  19. Rustenburg AS, Dancer J, Lin B et al (2016) Measuring experimental cyclohexane-water distribution coefficients for the SAMPL5 challenge. J Comput Aided Mol Des 30:945–958. https://doi.org/10.1007/s10822-016-9971-7

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  20. Bannan CC, Burley KH, Chiu M et al (2016) Blind prediction of cyclohexane–water distribution coefficients from the SAMPL5 challenge. J Comput Aided Mol Des 30:927–944. https://doi.org/10.1007/s10822-016-9954-8

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  21. Bannan CC, Mobley DL, Skillman AG (2018) SAMPL6 challenge results from pK a predictions based on a general Gaussian process model. J Comput Aided Mol Des 32:1165–1177. https://doi.org/10.1007/s10822-018-0169-z

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  22. Işık M, Levorse D, Mobley DL et al (2019) Octanol-water partition coefficient measurements for the SAMPL6 Blind Prediction Challenge. bioRxiv. https://doi.org/10.1101/757393

    Article  Google Scholar 

  23. Frisch MJ, Trucks GW, Schlegel HB et al (2009) Gaussian 09 Revision E.01. Gaussian 09, Revis. E.01. Gaussian, Wallingford

    Google Scholar 

  24. Ditchfield R, Hehre WJ, Pople JA (1971) Self consistent molecular orbital methods. IX. An extended Gaussian Type basis for molecular orbital studies of organic molecules. J Chem Phys 54:724–728. https://doi.org/10.1063/1.1674902

    Article  CAS  Google Scholar 

  25. Hehre WJ, Ditchfield K, Pople JA (1972) Self-consistent molecular orbital methods. XII. Further extensions of gaussian-type basis sets for use in molecular orbital studies of organic molecules. J Chem Phys. https://doi.org/10.1063/1.1677527

    Article  Google Scholar 

  26. Hariharan PC, Pople JA (1973) The influence of polarization functions on molecular orbital hydrogenation energies. Theor Chim Acta. https://doi.org/10.1007/BF00533485

    Article  Google Scholar 

  27. Hariharan PC, Pople JA (1974) Accuracy of AHn equilibrium geometries by single determinant molecular orbital theory. Mol Phys 27(1):209–214. https://doi.org/10.1080/00268977400100171

    Article  CAS  Google Scholar 

  28. Krishnan R, Binkley JS, Seeger R, Pople JA (1980) Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J Chem Phys 72(1):650–654. https://doi.org/10.1063/1.438955

    Article  CAS  Google Scholar 

  29. McLean AD, Chandler GS (1980) Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. J Chem Phys. https://doi.org/10.1063/1.438980

    Article  Google Scholar 

  30. Perdew JP (2003) Jacob’s ladder of density functional approximations for the exchange-correlation energy. AIP Publishing, College Park, pp 1–20

    Google Scholar 

  31. Becke AD (1993) Density-functional thermochemistry. III. The role of exact exchange. J Chem Phys 98:5648–5652. https://doi.org/10.1063/1.464913

    Article  CAS  Google Scholar 

  32. Lee C, Yang W, Parr RG (1988) Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B 37:785–789. https://doi.org/10.1103/PhysRevB.37.785

    Article  CAS  Google Scholar 

  33. Zhao Y, Truhlar DG (2008) The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor Chem Acc 120:215–241. https://doi.org/10.1007/s00214-007-0310-x

    Article  CAS  Google Scholar 

  34. Chai J, Da, Head-Gordon M (2008) Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys Chem Chem Phys 10:6615–6620. https://doi.org/10.1039/b810189b

    Article  CAS  PubMed  Google Scholar 

  35. Rayne S, Forest K (2010) Accuracy of computational solvation free energies for neutral and ionic compounds: dependence on level of theory and solvent model. Nat Preced. https://doi.org/10.1038/npre.2010.4864.1

    Article  Google Scholar 

  36. Bryantsev VS, Diallo MS, van Duin ACT, Goddard WA (2009) Evaluation of B3LYP, X3LYP, and M06-class density functionals for predicting the binding energies of neutral, protonated, and deprotonated water clusters. J Chem Theory Comput 5:1016–1026. https://doi.org/10.1021/ct800549f

    Article  CAS  PubMed  Google Scholar 

  37. Takano Y, Houk KN (2004) Benchmarking the conductor-like polarizable continuum model (CPCM) for Aqueous solvation free energies of neutral and ionic organic molecules. J Chem Theor Comput 1(1):70–77. https://doi.org/10.1021/CT049977A

    Article  Google Scholar 

  38. Kelly CP, Cramer CJ, Truhlar DG (2006) Aqueous solvation free energies of ions and ion – water clusters based on an accurate value for the absolute aqueous solvation free energy of the proton. J Phys Chem B 110(32):16066–16081. https://doi.org/10.1021/JP063552Y

    Article  CAS  PubMed  Google Scholar 

  39. Marenich AV, Cramer CJ, Truhlar DG (2009) Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J Phys Chem B 113:6378–6396. https://doi.org/10.1021/jp810292n

    Article  CAS  PubMed  Google Scholar 

  40. Marenich AV, Jerome SV, Cramer CJ, Truhlar DG (2012) Charge model 5: an extension of hirshfeld population analysis for the accurate description of molecular interactions in gaseous and condensed phases. J Chem Theory Comput. https://doi.org/10.1021/ct200866d

    Article  PubMed  Google Scholar 

  41. Skyner RE, McDonagh JL, Groom CR et al (2015) A review of methods for the calculation of solution free energies and the modelling of systems in solution. Phys Chem Chem Phys 17:6174–6191. https://doi.org/10.1039/c5cp00288e

    Article  CAS  PubMed  Google Scholar 

  42. Hansch C, Leo A, Hoek-man D (1996) Book reviews. J Med Chem 39:1189–1190

    Google Scholar 

  43. Borges NM, Kenny PW, Montanari CA et al (2017) The influence of hydrogen bonding on partition coefficients. J Comput Aided Mol Des 31:163–181. https://doi.org/10.1007/s10822-016-0002-5

    Article  CAS  PubMed  Google Scholar 

Download references

Acknowledgements

Calculations reported in this paper were partially performed using the computational resources at CCBG funded by Bogazici University and as well as the resources of the TUBITAK ULAKBIM High Performance and Grid Computing Center (TRUBA resources).

Author information

Authors and Affiliations

  1. Department of Chemistry, Bogazici University, 34342, Bebek, Istanbul, Turkey

    Evrim Arslan, Basak K. Findik & Viktorya Aviyente

Authors
  1. Evrim Arslan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Basak K. Findik
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Viktorya Aviyente
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Viktorya Aviyente.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (DOCX 6617.3 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Arslan, E., Findik, B.K. & Aviyente, V. A blind SAMPL6 challenge: insight into the octanol-water partition coefficients of drug-like molecules via a DFT approach. J Comput Aided Mol Des 34, 463–470 (2020). https://doi.org/10.1007/s10822-020-00284-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10822-020-00284-3

Keywords