Skip to main content

Advertisement

Springer Nature Link
Log in

A new method for estimating the relative binding free energy, derived from a free energy variational principle for the Pim-1-kinase–ligand and FKBP–ligand systems

  • Published:
Journal of Computer-Aided Molecular Design Aims and scope Submit manuscript

Abstract

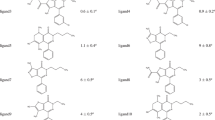
In this study, a new method is proposed for calculating the relative binding free energy between a ligand and a protein, derived from a free energy variational principle (FEVP). To address the shortcomings of the method used in our previous study, we incorporate the dynamical fluctuation of a ligand in the FEVP calculation. The present modified method is applied to the Pim-1-kinase–ligand system and also to the FKBP–ligand system as a comparison with our previous work. Any inhibitor of Pim-1 kinase is expected to function as an anti-cancer drug. Some improvements are observed in the results compared to the previous study. The present work also shows comparable or better results than approaches using a standard technique of binding free energy calculations, such as the LIE and the MM-PB/SA methods. The possibility of applying the present method in the drug discovery process is also discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Selassie CD (2003) History of quantitative structure–activity relationships. In: Abraham DJ (ed) Burger’s medicinal chemistry and drug discovery. Wiley, Hoboken, pp 1–96. https://doi.org/10.1002/0471266949.bmc001.pub2

    Chapter  Google Scholar 

  2. Åqvist J, Medina C, Samuelsson JE (1994) A new method for predicting binding affinity in computer-aided drug design. Protein Eng 7(3):385–391

    Article  PubMed  Google Scholar 

  3. Bohm HJ (1994) The development of a simple empirical scoring function to estimate the binding constant for a protein–ligand complex of known three-dimensional structure. J Comput Aided Mol Des 8(3):243–256

    Article  CAS  PubMed  Google Scholar 

  4. Apostolakis J, Caflisch A (1999) Computational ligand design. Comb Chem High Throughput Screen 2(2):91–104

    CAS  PubMed  Google Scholar 

  5. Talele TT, Khedkar SA, Rigby AC (2010) Successful applications of computer aided drug discovery: moving drugs from concept to the clinic. Curr Top Med Chem 10(1):127–141

    Article  CAS  PubMed  Google Scholar 

  6. Kapetanovic IM (2008) Computer-aided drug discovery and development (CADDD): in silico-chemico-biological approach. Chem Biol Interact 171(2):165–176. https://doi.org/10.1016/j.cbi.2006.12.006

    Article  CAS  PubMed  Google Scholar 

  7. Reddy MR, Erion MD, Agarwal A (2000) Free energy calculations: use and limitations in predicting binding affinities. In: Lipkowitz KB, Boyd DB (eds) Reviews in computational chemistry. Wiley, Hoboken

  8. Jayachandran G, Shirts MR, Park S, Pande VS (2006) Parallelized-over-parts computation of absolute binding free energy with docking and molecular dynamics. J Chem Phys 125(8):084901. https://doi.org/10.1063/1.2221680

    Article  CAS  PubMed  Google Scholar 

  9. Xu Y, Wang R (2006) A computational analysis of the binding affinities of FKBP12 inhibitors using the MM-PB/SA method. Proteins 64(4):1058–1068. https://doi.org/10.1002/prot.21044

    Article  CAS  PubMed  Google Scholar 

  10. Meng Y, Sabri Dashti D, Roitberg AE (2011) Computing alchemical free energy differences with Hamiltonian replica exchange molecular dynamics (H-REMD) simulations. J Chem Theory Comput 7(9):2721–2727. https://doi.org/10.1021/ct200153u

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  11. Genheden S, Ryde U (2015) The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin Drug Discov 10(5):449–461. https://doi.org/10.1517/17460441.2015.1032936

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  12. Sun H, Li Y, Tian S, Xu L, Hou T (2014) Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set. Phys Chem Chem Phys 16(31):16719–16729. https://doi.org/10.1039/c4cp01388c

    Article  CAS  PubMed  Google Scholar 

  13. Maffucci I, Contini A (2016) Improved computation of protein–protein relative binding energies with the Nwat-MMGBSA method. J Chem Inf Model 56(9):1692–1704. https://doi.org/10.1021/acs.jcim.6b00196

    Article  CAS  PubMed  Google Scholar 

  14. Cui YL, Zheng QC, Zhang JL, Xue Q, Wang Y, Zhang HX (2013) Molecular dynamic investigations of the mutational effects on structural characteristics and tunnel geometry in CYP17A1. J Chem Inf Model 53(12):3308–3317. https://doi.org/10.1021/ci400553w

    Article  CAS  PubMed  Google Scholar 

  15. Wallnoefer HG, Liedl KR, Fox T (2011) A challenging system: free energy prediction for factor Xa. J Comput Chem 32(8):1743–1752. https://doi.org/10.1002/jcc.21758

    Article  CAS  PubMed  Google Scholar 

  16. Genheden S, Ryde U (2012) Comparison of end-point continuum-solvation methods for the calculation of protein–ligand binding free energies. Proteins 80(5):1326–1342. https://doi.org/10.1002/prot.24029

    Article  CAS  PubMed  Google Scholar 

  17. Sun H, Duan L, Chen F, Liu H, Wang Z, Pan P, Zhu F, Zhang JZH, Hou T (2018) Assessing the performance of MM/PBSA and MM/GBSA methods. 7. Entropy effects on the performance of end-point binding free energy calculation approaches. Phys Chem Chem Phys 20(21):14450–14460. https://doi.org/10.1039/C7CP07623A

    Article  CAS  PubMed  Google Scholar 

  18. Ashida T, Kikuchi T (2013) Estimation of relative binding free energy based on a free energy variational principle for the FKBP–ligand system. J Comput Aided Mol Des 27(6):479–490. https://doi.org/10.1007/s10822-013-9657-3

    Article  CAS  PubMed  Google Scholar 

  19. Merkel AL, Meggers E, Ocker M (2012) PIM1 kinase as a target for cancer therapy. Expert Opin Investig Drugs 21(4):425–436. https://doi.org/10.1517/13543784.2012.668527

    Article  CAS  PubMed  Google Scholar 

  20. Bachmann M, Moroy T (2005) The serine/threonine kinase Pim-1. Int J Biochem Cell Biol 37(4):726–730. https://doi.org/10.1016/j.biocel.2004.11.005

    Article  CAS  PubMed  Google Scholar 

  21. Zhukova Iu N, Alekseeva MG, Zakharevich NV, Shtil AA, Danilenko VN (2011) The Pim family of protein kinases: structure, functions and roles in hematopoietic malignancies. Mol Biol (Mosk) 45(5):755–764

    Article  CAS  Google Scholar 

  22. Liang C, Li YY (2014) Use of regulators and inhibitors of Pim-1, a serine/threonine kinase, for tumour therapy (review). Mol Med Rep 9(6):2051–2060. https://doi.org/10.3892/mmr.2014.2139

    Article  CAS  PubMed  Google Scholar 

  23. Swords R, Kelly K, Carew J, Nawrocki S, Mahalingam D, Sarantopoulos J, Bearss D, Giles F (2011) The Pim kinases: new targets for drug development. Curr Drug Targets 12(14):2059–2066

    Article  CAS  PubMed  Google Scholar 

  24. Tursynbay Y, Zhang J, Li Z, Tokay T, Zhumadilov Z, Wu D, Xie Y (2016) Pim-1 kinase as cancer drug target: an update. Biomed Rep 4(2):140–146. https://doi.org/10.3892/br.2015.561

    Article  CAS  PubMed  Google Scholar 

  25. Shah N, Pang B, Yeoh KG, Thorn S, Chen CS, Lilly MB, Salto-Tellez M (2008) Potential roles for the PIM1 kinase in human cancer—a molecular and therapeutic appraisal. Eur J Cancer 44(15):2144–2151. https://doi.org/10.1016/j.ejca.2008.06.044

    Article  CAS  PubMed  Google Scholar 

  26. Burger MT, Nishiguchi G, Han W, Lan J, Simmons R, Atallah G, Ding Y, Tamez V, Zhang Y, Mathur M, Muller K, Bellamacina C, Lindvall MK, Zang R, Huh K, Feucht P, Zavorotinskaya T, Dai Y, Basham S, Chan J, Ginn E, Aycinena A, Holash J, Castillo J, Langowski JL, Wang Y, Chen MY, Lambert A, Fritsch C, Kauffmann A, Pfister E, Vanasse KG, Garcia PD (2015) Identification of N-(4-((1R,3S,5S)-3-amino-5-methylcyclohexyl)pyridin-3-yl)-6-(2,6-difluorophenyl)- 5-fluoropicolinamide (PIM447), a potent and selective proviral insertion site of moloney murine leukemia (PIM) 1, 2, and 3 kinase inhibitor in clinical trials for hematological malignancies. J Med Chem 58(21):8373–8386. https://doi.org/10.1021/acs.jmedchem.5b01275

    Article  CAS  PubMed  Google Scholar 

  27. Grey R, Pierce AC, Bemis GW, Jacobs MD, Moody CS, Jajoo R, Mohal N, Green J (2009) Structure-based design of 3-aryl-6-amino-triazolo[4,3-b]pyridazine inhibitors of Pim-1 kinase. Bioorg Med Chem Lett 19(11):3019–3022. https://doi.org/10.1016/j.bmcl.2009.04.061

    Article  CAS  PubMed  Google Scholar 

  28. Zuckerman DM (2010) Statistical physics of biomolecules. CRC Press, Boca Raton

    Book  Google Scholar 

  29. Feynman RP (1982) Statistical mechanics. A set of lectures. The Benjamin/Cummings Publishing Company, Reading

    Google Scholar 

  30. Michael P, Allen DJT (1987) Computer simulation of liquids. Oxford Science Publications, Oxford

    Google Scholar 

  31. Tucherman ME (2010) Statistical mechanics: theory and molecular simulation. Oxford Science Publications, Oxford

    Google Scholar 

  32. Zwanzig RW (1954) High-temperature equation of state by a perturbation method. I. Nonpolar gases. J Chem Phys 22:1420–1426

    Article  CAS  Google Scholar 

  33. Wang J, Wolf RM, Caldwell JW, Kollman PA, Case DA (2004) Development and testing of a general amber force field. J Comput Chem 25(9):1157–1174. https://doi.org/10.1002/jcc.20035

    Article  CAS  PubMed  Google Scholar 

  34. Jakalian A, Jack DB, Bayly CI (2002) Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J Comput Chem 23(16):1623–1641. https://doi.org/10.1002/jcc.10128

    Article  CAS  PubMed  Google Scholar 

  35. Maier JA, Martinez C, Kasavajhala K, Wickstrom L, Hauser KE, Simmerling C (2015) ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J Chem Theory Comput 11(8):3696–3713. https://doi.org/10.1021/acs.jctc.5b00255

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  36. Case DA, Babin V, Berryman JT, Betz RM, Cai Q, Cerutti DS, Cheatham TE, Darden TA, Duke RE, Gohlke HG, Goetz AW, Gusarov S, Homeyer N, Janowski P, Kaus J, Kolossváry I, Kovalenko A, Lee TS, LeGrand S, Luchko T, Luo R, Madej B, Merz KM, Paesani F, Roe DR, Roitberg A, Sagui C, Salomon-Ferrer R, Seabra G, Simmerling CL, Smith W, Swails J, Walker RC, Wang J, Wolf RM, Wu X, Kollman PA (2014) AMBER 14. University of California, San Francisco

    Google Scholar 

  37. Darden T, York D, Pedersen L (1993) Particle mesh Ewald: an NLog(N) method for Ewald sums in large systems. J Chem Phys 98:10089–10092

    Article  CAS  Google Scholar 

  38. Kollman PA, Massova I, Reyes C, Kuhn B, Huo S, Chong L, Lee M, Lee T, Duan Y, Wang W, Donini O, Cieplak P, Srinivasan J, Case DA, Cheatham TE 3rd (2000) Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc Chem Res 33(12):889–897

    Article  CAS  PubMed  Google Scholar 

  39. Miller BR, McGee TD, Swails JM, Homeyer N, Gohlke H, Roitberg AE (2012) MMPBSA.py: an efficient program for end-state free energy calculations. J Chem Theory Comput 8(9):3314–3321. https://doi.org/10.1021/ct300418h

    Article  CAS  PubMed  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Bioinformatics, College of Life Sciences, Ritsumeikan University, 1-1-1 Nojihigashi, Kusatsu, Shiga, 525-8577, Japan

    Takeshi Ashida & Takeshi Kikuchi

Authors
  1. Takeshi Ashida
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Takeshi Kikuchi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Takeshi Kikuchi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Electronic supplementary material 1 (DOCX 79 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ashida, T., Kikuchi, T. A new method for estimating the relative binding free energy, derived from a free energy variational principle for the Pim-1-kinase–ligand and FKBP–ligand systems. J Comput Aided Mol Des 34, 647–658 (2020). https://doi.org/10.1007/s10822-020-00302-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10822-020-00302-4

Keywords