A computational study of synaptic mechanisms of partial memory transfer in cerebellar vestibulo-ocular-reflex learning

Abstract

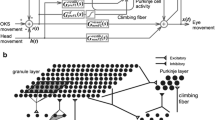
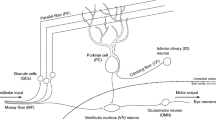
There is a debate regarding whether motor memory is stored in the cerebellar cortex, or the cerebellar nuclei, or both. Memory may be acquired in the cortex and then be transferred to the cerebellar nuclei. Based on a dynamical system modeling with a minimal set of variables, we theoretically investigated possible mechanisms of memory transfer and consolidation in the context of vestibulo-ocular reflex learning. We tested different plasticity rules for synapses in the cerebellar nuclei and took robustness of behavior against parameter variation as the criterion of plausibility of a model variant. In the most plausible scenarios, mossy-fiber nucleus-neuron synapses or Purkinje-cell nucleus-neuron synapses are plastic on a slow time scale and store permanent memory, whose content is passed from the cerebellar cortex storing transient memory. In these scenarios, synaptic strengths are potentiated when the mossy-fiber afferents to the nuclei are active during a pause in Purkinje-cell activities. Furthermore, assuming that mossy fibers create a limited variety of signals compared to parallel fibers, our model shows partial memory transfer from the cortex to the nuclei.

Appendices

Appendix A: Fast–slow analysis with static MF and PF firing and MF–VN plasticity

When the vestibular signal is static, we set ω=0, θ= π/2, and hence set the vestibular signal sin(ωt + θ)=1. Given that the MF and PF firing rates are static with f(a)=1, we have <sin(ωt + θ)u> _i =<sin(ωt + θ)x> _i =<u> _i =<x> _i  = <ux ^t> _i,j =<xu ^t> _j,i =<xx ^t> _i,j =1. Here, <u> _i , for example, is time average of the i-th MF signal. Because the PC–VN synapse is assumed to be static under MF–VN plasticity, we set b = 1. Let us assume m = n = 1 (and quit bold notations) and perform fast–slow analysis. Similar analysis works for general m and n.

In an early stage of learning, the PF–PC synapse w evolves much faster than the MF–VN synapse v does. The fast nullcline defined by setting dw/dt = 0 in Eq. (8) is given by

$$ v = v_{0} + R - R_{0} + \frac{{\eta _{1} + \eta _{3} }} {{\eta _{1} }}{\left( {w - w_{0} } \right)}. $$

(27)

On a short timescale, w and v converge onto this line.

1.1 A.1 CF-driven MF–VN plasticity

For the CF-driven learning, the slow nullcline to which w and v converge in a long run is given by setting dv/dt = 0 in Eq. (11):

$$ v = v_{0} + \frac{{\eta _{4} }} {{\eta _{4} + \eta _{6} }}{\left( {R - R_{0} } \right)} + \frac{{\eta _{4} }} {{\eta _{4} + \eta _{6} }}{\left( {w - w_{0} } \right)}. $$

(28)

A trajectory of the synaptic weights in the w–v plane approaches somewhere on the fast nullcline (Eq. (27)) and then slides along it toward the equilibrium obtained as the crossing of the two nullclines. The crossing is given by

$$ w^{*} = w_{0} - \frac{{\eta _{1} \eta _{6} {\left( {R - R_{0} } \right)}}} {{\eta _{1} \eta _{6} + \eta _{3} \eta _{4} + \eta _{3} \eta _{6} }}, $$

(29)

$$ v^{*} = v_{0} + \frac{{\eta _{3} \eta _{4} {\left( {R - R_{0} } \right)}}} {{\eta _{1} \eta _{6} + \eta _{3} \eta _{4} + \eta _{3} \eta _{6} }}. $$

(30)

The error at the equilibrium is

$$\begin{aligned} & e^{*} = R - v^{*} + w^{*} + y_{0} - z_{0} \\ & = \frac{{\eta _{3} \eta _{6} {\left( {R - R_{0} } \right)}}}{{\eta _{1} \eta _{6} + \eta _{3} \eta _{4} + \eta _{3} \eta _{6} }}, \\ \end{aligned} $$

(31)

which is small given η ₁ ≫ η ₃.

1.2 A.2 Hebbian MF–VN plasticity

For the Hebbian learning, the w-nullcline is given by Eq. (27), and the v-nullcline derived from Eq. (13) becomes

$$ v = v_{0} + \frac{{\eta _{4} }} {{\eta _{4} - \eta _{6} }}{\left( {w - w_{0} } \right)}. $$

(32)

The equilibrium is given by

$$ w^{*} = w_{0} + \frac{{\eta _{1} {\left( {\eta _{4} - \eta _{6} } \right)}{\left( {R - R_{0} } \right)}}} {{\eta _{1} \eta _{6} - \eta _{3} \eta _{4} + \eta _{3} \eta _{6} }}, $$

(33)

$$ v^{*} = v_{0} + \frac{{\eta _{1} \eta _{4} {\left( {R - R_{0} } \right)}}} {{\eta _{1} \eta _{6} - \eta _{3} \eta _{4} + \eta _{3} \eta _{6} }}, $$

(34)

$$ e^{*} = \frac{{\eta _{3} {\left( { - \eta _{4} + \eta _{6} } \right)}{\left( {R - R_{0} } \right)}}} {{\eta _{1} \eta _{6} - \eta _{3} \eta _{4} + \eta _{3} \eta _{6} }}. $$

(35)

Because the relative magnitudes of η ₁ η ₆ and η ₃ η ₄ are indecisive, the sign of η ₁ η ₆ − η ₃ η ₄ + η ₃ η ₆ is indefinite.

1.3 A.3 PC-driven MF–VN plasticity

For the PC-driven learning, the slow nullcline derived from Eq. (15) becomes

$$ v = v_{0} - \frac{{\eta _{4} }} {{\eta _{6} }}{\left( {w - w_{0} } \right)}, $$

(36)

and the equilibrium is given by

$$ w^{*} = w_{0} - \frac{{\eta _{1} \eta _{6} {\left( {R - R_{0} } \right)}}} {{\eta _{1} \eta _{4} + \eta _{1} \eta _{6} + \eta _{3} \eta _{6} }}, $$

(37)

$$ v^{*} = v_{0} + \frac{{\eta _{1} \eta _{4} {\left( {R - R_{0} } \right)}}} {{\eta _{1} \eta _{4} + \eta _{1} \eta _{6} + \eta _{3} \eta _{6} }}, $$

(38)

$$ e^{*} = \frac{{\eta _{3} \eta _{6} {\left( {R - R_{0} } \right)}}} {{\eta _{1} \eta _{4} + \eta _{1} \eta _{6} + \eta _{3} \eta _{6} }}. $$

(39)

Appendix B: Fast–slow analysis for PC-driven PC–VN plasticity

For PC-driven PC–VN plasticity, we can analytically obtain the equilibrium solutions. The initial synaptic weights are w = w ₀, v = v ₀, and b = b ₀, which are chosen to yield the initial gain R ₀. This condition together with Eqs. (16) and (18) provides the relations:

$$ R_{0} - v_{0} + b_{0} {\left( {w_{0} + y_{0} } \right)} - z_{0} = 0, $$

(40)

$$\kern6pt \eta _{4} {\left( {w_{0} + y_{0} - y_{{ref}} } \right)} - \eta _{6} b_{0} = 0. $$

(41)

Because we assumed η ₁ ≫ η ₃ and η ₄ ≫ η ₆, there are two equilibria (w*, b*) given by

$$ {\left( {w_{0} - \frac{{\eta _{6} {\left( {R - v_{0} } \right)}}} {{\eta _{4} {\left( {w_{0} + y_{0} } \right)}}},\frac{{v_{0} - R}} {{w_{0} + y_{0} }}} \right)} $$

(42)

and

$${\left( { - y_{0} + \frac{{\eta _{6} {\left( {R - v_{0} - z_{0} } \right)}}}{{\eta _{4} {\left( {w_{0} + y_{0} } \right)}}},b_{0} - \frac{{\eta _{4} {\left( {w_{0} + y_{0} } \right)}}}{{\eta _{6} }} + \frac{{R - v_{0} - z_{0} }}{{w_{0} + y_{0} }}} \right)}.$$

(43)

In both solutions, the final error is

$$ e^{*} = \frac{{\eta _{6} {\left( {R - v_{0} - z_{0} } \right)}{\left( {R - R_{0} } \right)}}} {{\eta _{4} {\left( {w_{0} + y_{0} } \right)}^{2} }}, $$

(44)

which is small. We discard the second solution because it is unstable.

Appendix C: Gain and phase learning with dynamic neural responses and MF–VN plasticity

With f(a) = sin(a), we obtain <x> = <u> = 0, <sin(ωt + θ)x> _i  = cos(θ − φ _i )/2, <xu ^t> _i,j =<ux ^t> _j,i =cos(ψ _j  − φ _i )/2, and <xx ^t> _i,j =cos(φ _j  − φ _i )/2. The signals with closer phase leads are more correlated. Then, Eq. (8) reads

$$\frac{{{\text{d}}w_{i} }}{{{\text{d}}t}} = - \frac{{\eta _{1} }}{2}{\left[ {{\left( {R - R_{0} } \right)}\cos {\left( {\theta - \phi _{i} } \right)} - {\sum\limits_{j = 1}^m {\cos {\left( {\psi _{j} - \phi _{i} } \right)}{\left( {v_{j} - v_{{0j}} } \right)} + {\sum\limits_{j = 1}^n {\cos {\left( {\phi _{j} - \phi _{i} } \right)}{\left( {w_{j} - w_{{0j}} } \right)}} }} }} \right]} - \eta _{3} n{\left( {w_{i} - w_{{0i}} } \right)}.$$

(45)

3.1 C.1 CF-driven MF–VN plasticity

With the CF-driven learning rule, Eq. (11) reads

$$\frac{{{\text{d}}v_{i} }}{{{\text{d}}t}} = \frac{{\eta _{4} }}{2}{\left[ {{\left( {R - R_{0} } \right)}\cos {\left( {\theta - \psi _{i} } \right)} - {\sum\limits_{j = 1}^m {\cos {\left( {\psi _{j} - \psi _{i} } \right)}{\left( {v_{j} - v_{{0j}} } \right)} + {\sum\limits_{j = 1}^n {\cos {\left( {\phi _{j} - \psi _{i} } \right)}{\left( {w_{j} - w_{{0j}} } \right)}} }} }} \right]} - \eta _{6} m{\left( {v_{i} - v_{{0i}} } \right)}.$$

(46)

In terms of the order parameters defined by

$$\begin{aligned} & W_{c} = {\sum\limits_{i = 1}^n {\cos \phi _{i} {\left( {w_{i} - w_{{0i}} } \right)}} },{\text{ }}W_{s} = {\sum\limits_{i = 1}^n {\sin \phi _{i} {\left( {w_{i} - w_{{0i}} } \right)}} }, \\ & V_{c} = {\sum\limits_{i = 1}^m {\cos \psi _{i} {\left( {v_{i} - v_{{0i}} } \right)}} },{\text{ V}}_{s} = {\sum\limits_{i = 1}^m {\sin \psi _{i} {\left( {v_{i} - v_{{0i}} } \right)}} }, \\ \end{aligned} $$

the equilibrium for the desired output R sin (ωt + θ) is obtained by solving

$$\begin{aligned} & \begin{array}{*{20}c} {{W^{*}_{c} }} & { = } & {{ - \frac{{\eta _{1} }}{{2\eta _{3} n}}\left[ {{\left( {R - R_{0} } \right)}\cos \theta {\sum\limits_{i = 1}^n {\cos ^{2} \phi _{i} + {\left( {R - R_{0} } \right)}\sin } }\theta {\sum\limits_{i = 1}^n {\cos \phi _{i} \sin \phi _{i} } }} \right.}} & {{}} \\ {{}} & {{}} & {{ + \left. {(W^{*}_{c} - V^{*}_{c} ){\sum\limits_{i = 1}^n {\cos ^{2} \phi _{i} + } }(W^{*}_{s} - V^{*}_{s} ){\sum\limits_{i = 1}^n {\cos \phi _{i} \sin \phi _{i} } }} \right],}} & {{}} \\ {{W^{*}_{s} }} & { = } & {{ - \frac{{\eta _{1} }}{{2\eta _{3} n}}\left[ {{\left( {R - R_{0} } \right)}\cos \theta {\sum\limits_{i = 1}^n {\cos \phi _{i} \sin \phi _{i} + {\left( {R - R_{0} } \right)}\sin } }\theta {\sum\limits_{i = 1}^n {\sin ^{2} \phi _{i} } }} \right.}} & {{}} \\ {{}} & {{}} & {{\left. { + {\left( {W^{*}_{c} - V^{*}_{c} } \right)}{\sum\limits_{i = 1}^n {\cos \phi _{i} \sin \phi _{i} + {\left( {W^{*}_{s} - V^{*}_{s} } \right)}} }{\sum\limits_{i = 1}^n {\sin ^{2} \phi _{i} } }} \right],}} & {{}} \\ \end{array} \\ & \begin{array}{*{20}c} {{V^{*}_{c} }} & { = } & {{\frac{{\eta _{4} }}{{2\eta _{6} m}}\left[ {{\left( {R - R_{0} } \right)}\cos \theta {\sum\limits_{i = 1}^m {\cos ^{2} \psi _{i} + {\left( {R - R_{0} } \right)}\sin } }\theta {\sum\limits_{i = 1}^m {\cos \psi _{i} \sin \psi _{i} } }} \right.}} & {{}} \\ {{}} & {{}} & {{\left. { + {\left( {W^{*}_{c} - V^{*}_{c} } \right)}{\sum\limits_{i = 1}^m {\cos ^{2} \psi _{i} + {\left( {W^{*}_{s} - V^{*}_{s} } \right)}} }{\sum\limits_{i = 1}^m {\cos \psi _{i} \sin \psi _{i} } }} \right],}} & {{}} \\ {{V^{*}_{s} }} & { = } & {{\frac{{\eta _{4} }}{{2\eta _{6} m}}\left[ {{\left( {R - R_{0} } \right)}\cos \theta {\sum\limits_{i = 1}^m {\cos \psi _{i} \sin \psi _{i} + {\left( {R - R_{0} } \right)}\sin } }\theta {\sum\limits_{i = 1}^m {\sin ^{2} \psi _{i} } }} \right.}} & {{}} \\ {{}} & {{}} & {{\left. { + {\left( {W^{*}_{c} - V^{*}_{c} } \right)}{\sum\limits_{i = 1}^m {\cos \psi _{i} \sin \psi _{i} + } }{\left( {W^{*}_{s} - V^{*}_{s} } \right)}{\sum\limits_{i = 1}^m {\sin ^{2} \psi _{i} } }} \right].}} & {{}} \\ \end{array} \\ \end{aligned} $$

The phase leads φ _i and ψ _i are assumed to be distributed uniformly on [0,2π] and [−Δ _ψ , Δ _ψ ], respectively. Assuming that n and m are large, we have, for example,

$$ {\sum\limits_{i = 1}^n {\cos ^{2} } }\phi _{i} = \frac{n} {{2\pi }}{\int_0^{2\pi } {\frac{{1 + \cos 2\phi }} {{2\phi }}} }d\phi = \frac{n} {2}. $$

(47)

For notational convenience, we write A _c (Δ _ψ ) = 1 + sin 2Δ _ψ /2Δ _ψ and A _s (Δ _ψ ) = 1 − sin 2Δ _ψ /2Δ _ψ . We note that 1 ≤ A _c  ≤ 2, and A _s decreases in Δ _ψ . Particularly, A _s  ≅ 2Δ _ψ ²/3 becomes small as Δ _ψ  → 0. Then, the equilibrium is given by

$$ V^{*}_{\alpha } = \frac{{\eta _{3} \eta _{4} {\left( {R - R_{0} } \right)}\cos \theta A_{\alpha } {\left( {\Delta _{\psi } } \right)}}} {{\eta _{1} \eta _{6} + 4\eta _{3} \eta _{6} + \eta _{3} \eta _{4} A_{\alpha } {\left( {\Delta _{\psi } } \right)}}}, $$

(48)

$$ W^{*}_{\alpha } = - \frac{{\eta _{1} \eta _{6} {\left( {R - R_{0} } \right)}\cos \theta }} {{\eta _{1} \eta _{6} + 4\eta _{3} \eta _{6} + \eta _{3} \eta _{4} A_{\alpha } {\left( {\Delta _{\psi } } \right)}}}, $$

(49)

where α = c or s. The amount of the memory stored in the MF–VN synapses is given by

$${\sum\limits_{i = 1}^m {\sin {\left( {\omega t + \psi _{i} } \right)}{\left( {v^{*}_{i} - v^{*}_{{0i}} } \right)} = V^{*}_{c} \sin \omega t + V^{*}_{s} \cos \omega t = r_{D} {\left( {R - R_{0} } \right)}\sin {\left( {\omega t + \theta _{D} } \right)},} }$$

(50)

where

$$ r_{D} = {\sqrt {\frac{{\cos ^{2} \theta }} {{{\left[ {1 + \frac{{\eta _{1} \eta _{6} + 4\eta _{3} \eta _{6} }} {{\eta _{3} \eta _{4} A_{c} {\left( {\Delta _{\psi } } \right)}}}} \right]}^{2} }} + \frac{{\sin ^{2} \theta }} {{{\left[ {1 + \frac{{\eta _{1} \eta _{6} + 4\eta _{3} \eta _{6} }} {{\eta _{3} \eta _{4} A_{s} {\left( {\Delta _{\psi } } \right)}}}} \right]}^{2} }}} }, $$

(51)

$$ \theta _{D} = \tan ^{{ - 1}} {\left[ {\frac{{1 + \frac{{\eta _{1} \eta _{6} + 4\eta _{3} \eta _{6} }} {{\eta _{3} \eta _{4} A_{c} {\left( {\Delta _{\psi } } \right)}}}}} {{1 + \frac{{\eta _{1} \eta _{6} + 4\eta _{3} \eta _{6} }} {{\eta _{3} \eta _{4} A_{s} {\left( {\Delta _{\psi } } \right)}}}}}\tan \theta } \right]}. $$

(52)

If MFs create any delay elements (Δ _ψ  = π, A _c (Δ _ψ ) = A _s (Δ _ψ ) = 1), Eq. (52) results in θ _D  = θ, that is, the perfect phase learning by the MF–VN synapses. However, r _D  = η ₃ η ₄/(η ₁ η ₆ + η ₃ η ₄ + 4η ₃ η ₆) can be considerably smaller than the ideal value (= 1) because η ₁ η ₆ may be as large as η ₃ η ₄ in general. The MF–VN synapses learn the desired gain only for a restricted parameter range, and gain transfer is not robust against parameter variation. This is in line with the result of the gain-only theory.

Furthermore, the discrepancy between θ _D and θ cannot be ignored when Δ _ψ  = O((η ₁ η ₆/η ₃ η ₄)^1/2) i.e. when Δ _ψ is of the order of (η ₁ η ₆/η ₃ η ₄)^1/2. Because η ₁ ≫ η ₃ and η ₄ ≫ η ₆, one cannot tell without additional information whether η ₁ η ₆ ≫ η ₃ η ₄, η ₁ η ₆ ≅ η ₃ η ₄, or η ₁ η ₆ ≪ η ₃ η ₄. Because η ₁ η ₆/η ₃ η ₄ is not necessarily small, transfer can degrade even for a large Δ _ψ .

3.2 C.2 Hebbian MF–VN plasticity

With the Hebbian rule, Eq. (13) reads

$$\frac{{{\text{d}}v_{i} }}{{{\text{d}}t}} = \frac{{\eta _{4} }}{2}{\left[ {{\sum\limits_{j = 1}^m {\cos {\left( {\psi _{j} - \psi _{i} } \right)}{\left( {v_{j} - v_{{0j}} } \right)} - {\sum\limits_{j = 1}^n {\cos {\left( {\phi _{j} - \psi _{i} } \right)}{\left( {w_{j} - w_{{0j}} } \right)}} }} }} \right]} - \eta _{6} m{\left( {v_{i} - v_{{0i}} } \right)}.$$

(53)

By solving the equilibrium in combination with Eq. (45), we have

$$V^{*}_{\alpha } = \frac{{\eta _{1} \eta _{4} {\left( {R - R_{0} } \right)}\cos \theta A_{\alpha } {\left( {\Delta _{\psi } } \right)}}}{{ - 4\eta _{3} \eta _{4} A_{\alpha } {\left( {\Delta _{\psi } } \right)} + 4\eta _{1} \eta _{6} + 16\eta _{3} \eta _{6} }},$$

(54)

$$ W^{*}_{\alpha } = \frac{{\eta _{1} {\left( {R - R_{0} } \right)}\cos \theta {\left[ {\eta _{4} A_{\alpha } {\left( {\Delta _{\psi } } \right)} - 4\eta _{6} } \right]}}} {{ - 4\eta _{3} \eta _{4} A_{\alpha } {\left( {\Delta _{\psi } } \right)} + 4\eta _{1} \eta _{6} + 16\eta _{3} \eta _{6} }}, $$

(55)

which leads to

$$ r_{D} = {\sqrt {\frac{{\cos ^{2} \theta }} {{{\left[ {\frac{{4\eta _{1} \eta _{6} + 16\eta _{3} \eta _{6} }} {{\eta _{1} \eta _{4} A_{c} {\left( {\Delta _{\psi } } \right)}}} - \frac{{4\eta _{3} }} {{\eta _{1} }}} \right]}^{2} }} + \frac{{\sin ^{2} \theta }} {{{\left[ {\frac{{4\eta _{1} \eta _{6} + 16\eta _{3} \eta _{6} }} {{\eta _{1} \eta _{4} A_{s} {\left( {\Delta _{\psi } } \right)}}} - \frac{{4\eta _{3} }} {{\eta _{1} }}} \right]}^{2} }}} }, $$

(56)

$$ \theta _{D} = \tan ^{{ - 1}} {\left[ {\frac{{\frac{{\eta _{1} \eta _{6} + 4\eta _{3} \eta _{6} }} {{\eta _{1} \eta _{4} A_{c} {\left( {\Delta _{\psi } } \right)}}} - \frac{{\eta _{3} }} {{\eta _{1} }}}} {{\frac{{\eta _{1} \eta _{6} + 4\eta _{3} \eta _{6} }} {{\eta _{1} \eta _{4} A_{s} {\left( {\Delta _{\psi } } \right)}}} - \frac{{\eta _{3} }} {{\eta _{1} }}}}\tan \theta } \right]}. $$

(57)

When MFs create any phase leads (Δ _ψ  = π), Eq. (57) implies perfect transfer of the target phase (θ _D  = θ). However, r _D  = η ₁ η ₄/(4η ₁ η ₆ + 16η ₃ η ₆ − 4η ₃ η ₄), derived from Eq. (56), is indefinite because 4η ₁ η ₆ + 16η ₃ η ₆ − 4η ₃ η ₄ can take an arbitrary value. Consequently, unrealistic phenomena such as overlearning (r _D  > 1) can arise in the model. Regarding phase learning, the error is prominent when Δ _ψ is as small as Δ _ψ  = O((η ₆/η ₄)^1/2) (recall η ₄ ≫ η ₆), which is suitable.

3.3 C.3 PC-driven MF–VN plasticity

With the PC-driven learning, Eq. (15) reads

$$\frac{{dv_{i} }}{{dt}} = - \frac{{\eta _{4} }}{2}{\sum\limits_{j = 1}^n {\cos {\left( {\phi _{j} - \psi _{i} } \right)}{\left( {w_{j} - w_{{0j}} } \right)}} } - \eta _{6} m{\left( {v_{i} - v_{{0i}} } \right)}.$$

(58)

We derive

$$ V^{*}_{\alpha } = \frac{{\eta _{1} \eta _{4} {\left( {R - R_{0} } \right)}\cos \theta A_{\alpha } {\left( {\Delta _{\psi } } \right)}}} {{\eta _{1} \eta _{4} A_{\alpha } {\left( {\Delta _{\psi } } \right)} + 4\eta _{1} \eta _{6} + 16\eta _{3} \eta _{6} }}, $$

(59)

$$ W^{*}_{\alpha } = - \frac{{4\eta _{1} \eta _{6} {\left( {R - R_{0} } \right)}\cos \theta }} {{\eta _{1} \eta _{4} A_{\alpha } {\left( {\Delta _{\psi } } \right)} + 4\eta _{1} \eta _{6} + 16\eta _{3} \eta _{6} }}, $$

(60)

which in combination with Eq. (50) yields r _D (Eq. (23)) and θ _D (Eq. (24)). The amount of the memory stored in the PF–PC synapses is represented by

$$ - W^{*}_{c} \sin \omega t - W^{*}_{s} \cos \omega t = r_{I} {\left( {R - R_{0} } \right)}\sin {\left( {\omega t + \theta _{I} } \right)}, $$

(61)

which yields r _I (Eq. (25)) and θ _I (Eq. (26)).