Spectrum of Lyapunov exponents of non-smooth dynamical systems of integrate-and-fire type

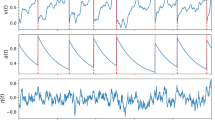
Abstract

We discuss how to characterize long-time dynamics of non-smooth dynamical systems, such as integrate-and-fire (I&F) like neuronal network, using Lyapunov exponents and present a stable numerical method for the accurate evaluation of the spectrum of Lyapunov exponents for this large class of dynamics. These dynamics contain (i) jump conditions as in the firing-reset dynamics and (ii) degeneracy such as in the refractory period in which voltage-like variables of the network collapse to a single constant value. Using the networks of linear I&F neurons, exponential I&F neurons, and I&F neurons with adaptive threshold, we illustrate our method and discuss the rich dynamics of these networks.

Appendix: Proof of no degeneracy in the augmented dynamics

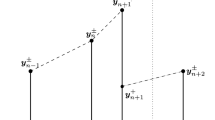
Here, we demonstrate that the introduction of the dynamics of the refractory residence time indeed extends the original standard algorithm of computing LEs and does not encounter the degeneracy problem as discussed before. In other words, we can show that evolving from an initial ball with radius ε centered at the reference trajectory to any time T, one can always obtain a linear transformed ellipsoid without degeneracy.

Suppose at time T ⁽ⁿ⁾ = nΔ T, the system is in the network subthreshold period and the perturbation vector $\delta{\boldsymbol{x}}^{(n)}$ is given as $(\delta{\boldsymbol{x}}^{(n)}_1, \delta{\boldsymbol{x}}^{(n)}_2,\cdots,\delta{\boldsymbol{x}}^{(n)}_N)$, where $\delta{\boldsymbol{x}}^{(n)}_i\!=\!(\delta{V}_i^{(n)},\delta{G}_i^{(n)})$. Then, at the next time T ^(n + 1) = (n + 1)ΔT, the system is in the network refractory period with the perturbation vector $\delta{\boldsymbol{x}}^{(n+1)}\!=$ $(\delta{\boldsymbol{x}}^{(n+1)}_1, \delta{\boldsymbol{x}}^{(n+1)}_2,\cdots,\delta{\boldsymbol{x}}^{(n+1)}_N)$, where $\delta{\boldsymbol{x}}^{(n+1)}_i \!=\! (\delta{\tau}_i^{(n+1)},$ $\delta{G}_i^{(n+1)})$ if $T^{(n+1)}\in \bigcup\limits_k(T_{i,k},T_{i,k}+\tau_{\rm{ref}})$ and $\delta{\boldsymbol{x}}^{(n+1)}_i = (\delta{V}_i^{(n+1)},\delta{G}_i^{(n+1)})$ if $T^{(n+1)}\in\bigcup\limits_k(T_{i,k}+\tau_{\rm{ref}},\,T_{i,k+1})$. We show that there is no degeneracy problem when using GSR at time T ^(n + 1) to obtain the local LEs of the system. In other words, the evolution matrix $\mathbb{A}^{(n,n+1)}$ over the interval [T ⁽ⁿ⁾,T ^(n + 1)] linking the perturbation vector from $\delta{\boldsymbol{x}}^{(n)}$ to $\delta{\boldsymbol{x}}^{(n+1)}$ is nondegenerate (nonsingular). We first divide the interval [T ⁽ⁿ⁾,T ^(n + 1)] into the combination of several subintervals as $[T^{(n)},T^{(n+1)}]\!=\!\bigcup\limits_{i=0}^{M-1}\bar{E}_{i}$, where $\bar{E}_i\!=\![T^{(n_i)},$ $T^{(n_{i+1})}]$ with n ₀ = n, n _M  = n + 1, and $T^{(n)}<T^{(n_i)}<T^{(n+1)}\,(i=1,2,\cdots,M-1)$ are chosen from either the set of neurons’ spike time $\bigcup\limits_j\bigcup\limits_k\{T_{j,k}\}$ or the set of neurons’ awakening time $\bigcup\limits_j\bigcup\limits_k\{T_{j,k}+\tau_{\rm{ref}}\}$. Notice that the dynamics of the perturbation vector over each subinterval $E_i=(T^{(n_i)},T^{(n_{i+1})})$ is smooth, we will show that both the evolution matrix $\mathbb{B}^{(n_i,n_{i+1})}$ over each subinterval linking the perturbation vector from $\delta{\boldsymbol{x}}^{(n_i^{+})}$ to $\delta{\boldsymbol{x}}^{(n_{i+1}^{-})}$ and the transition matrix $\mathbb{R}^{(n_i}$ immediately before and after each $T^{(n_i)}$ linking the perturbation vector from $\delta{\boldsymbol{x}}^{(n_i^{-})}$ to $\delta{\boldsymbol{x}}^{(n_i^{+})}$ are nondegenerate, where $\delta{\boldsymbol{x}}^{(n_i^{+})}$ and $\delta{\boldsymbol{x}}^{(n_{i+1}^{-})}$ represent one-sided limits of the perturbation vector $\delta{\boldsymbol{x}}$ obtained as $\lim\limits_{{T-T^{(n_i)}\rightarrow{0^{+}}}}\delta{\boldsymbol{x}}(T)$ and $\lim\limits_{{T-T^{(n_{i+1})}\rightarrow{0^{-}}}}\delta{\boldsymbol{x}}(T)$. For any n _i (i = 1,2, ⋯ ,M − 1), we first consider the transition matrix $\mathbb{R}^{(n_i}$ immediately before and after $T^{(n_i)}$. (i) If $T^{(n_i)}=T_{j,k}$ (the kth spike time of the jth neuron), the transition matrix $\mathbb{R}^{(n_i}$ can be obtained as

$$ \label{TranMatrix1} \mathbb{R}^{(n_i)}(p,q) = \begin{cases} \qquad{1}& \text{if $p=q\neq{2j-1}$,}\\ \frac{1}{\dot{V}_j(T_{j,k}^{-})}& \text{if $p=q=2j-1$,}\\ -\frac{S}{\sigma{\dot{V}_j(T_{j,k}^{-})}}& \text{if $q=2j-1$ and $p$ is even}, \\ & \quad\text{but $p\neq{2j}$,}\\ \qquad{0}& \text{otherwise,} \end{cases} $$

(20)

where $\mathbb{R}^{(n_i}$ represents the element of the matrix with the position at the pth row and the qth column. The first line on the RHS of Eq. (20) describes the linear transition coefficient of the lth neuron’s voltage component in the perturbation vector linking $\delta{V}_l^{(n_i^{-})}$ and $\delta{V}_l^{(n_i^{+})}$ with the label l ≠ j. The second line on the RHS of Eq. (20) describes the linear transition coefficient of the jth neuron’s voltage component in the perturbation vector linking $\delta{V}_j^{(n_i^{-})}$ and $\delta{\tau}_j^{(n_i^{+})}$ as in Eq. (13). The third line combined with the first line on the RHS of Eq. (20) describes the linear transition coefficients of the lth neuron’s conductance component in the perturbation vector linking $\delta{G}_l^{(n_i^{-})}$ and $\delta{G}_l^{(n_i^{+})}$ with the label l ≠ j as in Eq. (10) (we only consider the effects of the jth neuron’s spike to the change of other neurons’ conductance, not to itself). (ii) If $T^{(n_i)}=T_{j,k}+\tau_{\rm{ref}}$ (the kth awakening time of the jth neuron), the transition matrix $\mathbb{R}^{(n_i}$ can be obtained as

$$ \label{TranMatrix2} \mathbb{R}^{(n_i)}(p,q) = \begin{cases} \qquad{1}& \text{if $p=q\neq{2j-1}$,}\\ \dot{V}_j\bigl[(T_{j,k}+\tau_{\rm{ref}})^{+}\bigr] & \text{if $p=q=2j-1$}, \\ \qquad{0}& \text{otherwise,} \end{cases} $$

(21)

where the first line on the RHS of Eq. (21) describes the linear transition coefficient of the lth neuron’s voltage component in the perturbation vector linking $\delta{V}_l^{(n_i^{-})}$ and $\delta{V}_l^{(n_i^{+})}$ with the label l ≠ j, and also the linear transition coefficient of the lth neuron’s conductance component in the perturbation vector linking $\delta{G}_l^{(n_i^{-})}$ and $\delta{G}_l^{(n_i^{+})}$ with the label l = 1,2, ⋯ ,N. The second line on the RHS of Eq. (21) describes the linear transition coefficient of the jth neuron’s voltage component in the perturbation vector linking $\delta{\tau}_j^{(n_i^{-})}$ and $\delta{V}_j^{(n_i^{+})}$ as in Eq. (14). We can see that the transition matrix is nondegenerate in both cases (i) and (ii). Next, we consider the evolution matrix $\mathbb{B}^{(n_i,n_{i+1})}$ over each subinterval E _i . For any n _i (i = 0,1, ⋯ ,M − 1), we define two sets of neuron index for a given E _i as follows: the first set I is given as $I=\{j|1\leq{j}\leq{N},\,E_i\subseteq{\Gamma_j}\}$, where Γ _j is the set of the jth neuron’s refractory period as $\Gamma_j=\bigcup\limits_k(T_{j,k},T_{j,k}+\tau_{\rm{ref}})$. The second set J is given as $J=\{j|1\leq{j}\leq{N},\,E_i\subseteq{\Lambda_j}\}$ , where Λ _j is the set of the jth neuron’s subthreshold period as $\Lambda_j=\bigcup\limits_k(T_{j,k}+\tau_{\rm{ref}},T_{j,k+1})$. The evolution matrix $\mathbb{B}^{(n_i,n_{i+1})}$ can be obtained as $\mathbb{B}^{(n_i,n_{i+1})}(p,q) =$

$$ \label{EvolMatrix} \begin{cases} &\exp\Bigl(-\int_{E_{i}}\bigl[G^{L}+G_l(s)\bigr]\,ds\Bigr), \\ &\qquad\qquad \text{if $p=q=2l-1$, where $l\in{J}$;}\\ &-\int_{E_i}{\exp\bigl[-\Psi(s)\bigr] \bigl[V_l(s)-V^{E}\bigr]\,ds}, \\ &\qquad\qquad \text{if $p+1=q=2l$, where $l\in{J}$;}\\ &\exp\bigl(-\frac{T^{(n_{i+1})}-T^{(n_{i})}}{\sigma}\bigr), \\ &\qquad\qquad \text{if $p=q=2l$, where $1\leq{l}\leq{N}$;}\\ &{1}, \qquad\quad \text{if $p=q=2l-1$, where $l\in{I}$;}\\ &{0}, \qquad\quad \text{otherwise,} \end{cases} $$

(22)

where

$$ \Psi(s)= \int_{s}^{T^{(n_{i+1})}}\bigl[G^{L}+G_l(w)\bigr]\,dw+\frac{s-T^{(n_i)}}{\sigma}. $$

The first line and the second line on the RHS of Eq. (22) describe the linear transition coefficients of the lth neuron’s voltage component in the perturbation vector linking $\delta{V}_l^{(n_i^{-})}$, $\delta{G}_l^{(n_i^{-})}$ and $\delta{V}_l^{(n_i^{+})}$ as obtained by linearization of Eq. (5) with the label l ∈ J (i.e., the neuron under its subthreshold dynamics). The third line on the RHS of Eq. (22) describes the linear transition coefficient of the lth neuron’s conductance component in the perturbation vector linking $\delta{G}_l^{(n_i^{-})}$ and $\delta{G}_l^{(n_i^{+})}$ with the label l = 1,2, ⋯ ,N. The fourth line on the RHS of Eq. (22) describes the linear transition coefficient of the lth neuron’s voltage component in the perturbation vector linking $\delta{\tau}_l^{(n_i^{-})}$ and $\delta{\tau}_l^{(n_i^{+})}$ with the label l ∈ I (i.e., the neuron under its refractory dynamics). We can see that the evolution matrix $\mathbb{B}^{(n_i,n_{i+1})}$ is also nondegenerate. The evolution matrix $\mathbb{A}^{(n)}$ over the whole interval [T ⁽ⁿ⁾,T ^(n + 1)] should be the product of both the evolution matrix over each subinterval $(T^{(n_i)},T^{(n_{i+1})})$ and the transition matrix immediately before and after each $T^{(n_i)}$ as $\mathbb{A}^{(n)}=\mathbb{B}^{(n_0,n_1)}\mathbb{R}^{(n_1)}\times \mathbb{B}^{(n_1,n_2)}\mathbb{R}^{(n_2)}\cdots\mathbb{R}^{(n_{M-1})} \mathbb{B}^{(n_{M-1},n_M)}$. Therefore, the evolution matrix $\mathbb{A}^{(n)}$ is nondegenerate and we will not encounter the degeneracy problem when computing the local LEs using GSR. This is because we can always generate a complete set of corresponding orthogonal vectors at time T ^(n + 1) even though T ^(n + 1) is in a network refractory period. As a conclusion, both the theoretical definition and the numerical algorithm of LEs for smooth dynamical systems can be extended to the non-smooth dynamical systems of I&F networks with refractory-induced degeneracy.