Quadratic sinusoidal analysis of voltage clamped neurons

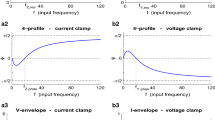
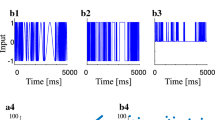
Abstract

Nonlinear biophysical properties of individual neurons are known to play a major role in the nervous system, especially those active at subthreshold membrane potentials that integrate synaptic inputs during action potential initiation. Previous electrophysiological studies have made use of a piecewise linear characterization of voltage clamped neurons, which consists of a sequence of linear admittances computed at different voltage levels. In this paper, a fundamentally new theory is developed in two stages. First, analytical equations are derived for a multi-sinusoidal voltage clamp of a Hodgkin–Huxley type model to reveal the quadratic response at the ionic channel level. Second, the resulting behavior is generalized to a novel Hermitian neural operator, which uses an algebraic formulation capturing the entire quadratic behavior of a voltage clamped neuron. In addition, this operator can also be used for a nonlinear identification analysis directly applicable to experimental measurements. In this case, a Hermitian matrix of interactions is built with paired frequency probing measurements performed at specific harmonic and interactive output frequencies. More importantly, eigenanalysis of the neural operator provides a concise signature of the voltage dependent conductances determined by their particular distribution on the dendritic and somatic membrane regions of neurons. Finally, the theory is concretely illustrated by an analysis of an experimentally measured vestibular neuron, providing a remarkably compact description of the quadratic responses involved in the nonlinear processing underlying the control of eye position during head rotation, namely the neural integrator.