An L ₁-regularized logistic model for detecting short-term neuronal interactions

Abstract

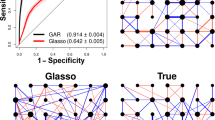
Interactions among neurons are a key component of neural signal processing. Rich neural data sets potentially containing evidence of interactions can now be collected readily in the laboratory, but existing analysis methods are often not sufficiently sensitive and specific to reveal these interactions. Generalized linear models offer a platform for analyzing multi-electrode recordings of neuronal spike train data. Here we suggest an L ₁-regularized logistic regression model (L ₁ L method) to detect short-term (order of 3 ms) neuronal interactions. We estimate the parameters in this model using a coordinate descent algorithm, and determine the optimal tuning parameter using a Bayesian Information Criterion. Simulation studies show that in general the L ₁ L method has better sensitivities and specificities than those of the traditional shuffle-corrected cross-correlogram (covariogram) method. The L ₁ L method is able to detect excitatory interactions with both high sensitivity and specificity with reasonably large recordings, even when the magnitude of the interactions is small; similar results hold for inhibition given sufficiently high baseline firing rates. Our study also suggests that the false positives can be further removed by thresholding, because their magnitudes are typically smaller than true interactions. Simulations also show that the L ₁ L method is somewhat robust to partially observed networks. We apply the method to multi-electrode recordings collected in the monkey dorsal premotor cortex (PMd) while the animal prepares to make reaching arm movements. The results show that some neurons interact differently depending on task conditions. The stronger interactions detected with our L ₁ L method were also visible using the covariogram method.

Appendix

The proof quotes two lemmas and theorems in Qian and Wu (2006), one theorem in Fan and Li (2001) and one theorem in Park and Hastie (2007). To make them hold, we inherit the conditions (C.1)–(C.14) in Qian and Wu (2006) and conditions (A)–(C) in Fan and Li (2001). We refer the reader to those papers for the details. Without elaborating those conditions, we paraphrase the quoted lemmas and theorems as the lemmas for our proof. Intuitively, the conditions (C.1)–(C.6) are requirements for link functions in general, which logit link will not violate (Qian and Wu 2006). The conditions (C.7)–(C.13) are requirements for covariates, where no observation should dominate as the sample size tends to infinity. The conditions (C.14) and (A)–(C) are requirements for log-likelihood functions, where classic likelihood theory can apply.

We denote $\boldsymbol\beta_0$ as the true values of a collection of P parameters, of which only p are nonzero. Here we assume both p and P finite and not varying with sample size n. Denote the log-likelihood function for logistic regression as l. $\mathcal{C}$ and $\mathcal{W}$ are sets of all correct models and all wrong models respectively. $\hat{\boldsymbol\beta}_c$ stands for the unregularized MLEs under the assumption of model $c\in\mathcal{C}$, and $\hat{\boldsymbol\beta}_w$ stands for the unregularized MLEs under the assumption of model $w\in\mathcal{W}$. $\hat{\boldsymbol\beta}(\gamma)$ stands for the L ₁-regularized estimates at γ. If there is a subscript c or w under $\hat{\boldsymbol\beta}(\gamma)$, it means that the nonzero estimates in $\hat{\boldsymbol\beta}(\gamma)$ consist of model c or w.

Lemma 1

(Theorem 2 in Qian and Wu 2006) Under (C.1)–(C.14), for any correct model $c\in\mathcal{C}$

$$ 0\leq l\left(\hat{\boldsymbol\beta}_c\right)-l(\boldsymbol\beta_0)=O(\log\log n), \mbox{\ a.s..} $$

Lemma 2

(Theorem 3 in Qian and Wu 2006) Under (C.1)–(C.14), for any wrong model $w\in\mathcal{W}$

$$ 0< l(\boldsymbol\beta_0)-l\left(\hat{\boldsymbol\beta}_w\right)=O(n), \mbox{\ a.s..} $$

Lemma 3

(Theorem 1 in Fan and Li 2001) Under (A)–(C), there exists a local maximizer $\hat{\boldsymbol\beta}(\gamma)$ for L ₁ -regularized log-likelihood such that $\parallel\hat{\boldsymbol\beta}(\gamma)-\boldsymbol\beta_0\parallel=O_p(n^{-1/2}+\gamma/n)$ .

Lemma 4

(Lemma 4 in Qian and Wu 2006) Under (C.1)–(C.14), we have each component of $\frac{\partial l}{\partial\boldsymbol\beta}(\boldsymbol\beta_0)$ equal to $O(\sqrt{n\log\log n})$ a.s..

Lemma 5

(Lemma 6 in Qian and Wu 2006) Under (C.1)–(C.14), there exists two positive numbers d ₁ and d ₂ such that the eigenvalues of $-\partial^2l/\partial\boldsymbol\beta\partial\boldsymbol\beta'$ at $\boldsymbol\beta_0$ are bounded by d ₁ n and d ₂ n a.s. as n goes to infinity.

Lemma 6

(Lemma 1 in Park and Hastie 2007) If the intercept in the logistic model are not regularized, when $\gamma>\max\mid(\frac{\partial l}{\partial\boldsymbol\beta})_j\mid$ ,j = 1, ..., P, the intercept is the only non-zero coefficient.

Proof of the Theorem

Let γ ₁ > γ ₂. Denote m ₁ as the model consisting of d ₁ nonzero parameters in $\hat{\boldsymbol\beta}(\gamma_1)$, and m ₂ as the model consisting of d ₂ nonzero parameters in $\hat{\boldsymbol\beta}(\gamma_2)$. Therefore,

$$ \begin{array}{rll} BIC(\gamma_1)-BIC(\gamma_2) & = & -2l(\hat{\boldsymbol\beta}(\gamma_1))+d_1\log n\\ &&-\,\left[-2l\left(\hat{\boldsymbol\beta}(\gamma_2)\right)+d_2\log n\right]\\ & = & (d_1-d_2)\log n+2\left[l\left(\hat{\boldsymbol\beta}(\gamma_2)\right)\right.\\ &&\left.-\, l(\hat{\boldsymbol\beta}(\gamma_1))\right]\\ & = & (d_1-d_2)\log n\\ & & +2\left[l(\hat{\boldsymbol\beta}(\gamma_2))-l(\hat{\boldsymbol\beta}_{m_2}) +l(\hat{\boldsymbol\beta}_{m_2})\right.\\ &&\left.-\, l\left(\hat{\boldsymbol\beta}_{m_1}\right) +l(\hat{\boldsymbol\beta}_{m_1})-l\left(\hat{\boldsymbol\beta}(\gamma_1)\right)\right] \end{array} $$

If $m_1\in\mathcal{C}$ and $m_2\in\mathcal{C}$, by Lemma 1, we have (d ₁ − d ₂)log n = O(log n) < 0 and $l(\hat{\boldsymbol\beta}_{m_2})-l(\hat{\boldsymbol\beta}_{m_1})=O(\log\log n)>0$. By the definition of maximum likelihood, we also have $l(\hat{\boldsymbol\beta}(\gamma_2))-l(\hat{\boldsymbol\beta}_{m_2})<0$. Therefore, as long as $l(\hat{\boldsymbol\beta}_{m_1})-l(\hat{\boldsymbol\beta}(\gamma_1))=o(\log n)$, BIC(γ ₁) − BIC(γ ₂) < 0 and the correct model m ₁ with smaller number of parameters is selected.

If $m_1\in\mathcal{W}$ and $m_2\in\mathcal{C}$, by Lemma 2, we have (d ₁ − d ₂)log n = O(log n) < 0 and $l(\hat{\boldsymbol\beta}_{m_2})-l(\hat{\boldsymbol\beta}_{m_1})=O(n)>0$. Again by the definition of maximum likelihood, we have $l(\hat{\boldsymbol\beta}_{m_1})-l(\hat{\boldsymbol\beta}(\gamma_1))>0$. Therefore, as long as $l(\hat{\boldsymbol\beta}(\gamma_2))-l(\hat{\boldsymbol\beta}_{m_2})=o(n)$, BIC(γ ₁) − BIC(γ ₂) > 0 and the correct model m ₂ is selected.

Thus, it is required to show that, for any $c\in\mathcal{C}$, we have $l(\hat{\boldsymbol\beta}_{c})-l(\hat{\boldsymbol\beta}_c(\gamma))=o(\log n)$. Because $l(\hat{\boldsymbol\beta}_{c})-l(\boldsymbol\beta_{0})=O(\log\log n)$, it suffices to show $l(\boldsymbol\beta_{0})-l(\hat{\boldsymbol\beta}_c(\gamma))=o(\log n)$. By a Taylor expansion, we have

$$ \begin{array}{rll} l(\boldsymbol\beta)-l(\boldsymbol\beta_{0}) &=& (\boldsymbol\beta-\boldsymbol\beta_{0})'\frac{\partial l(\boldsymbol\beta_0)}{\partial\boldsymbol\beta}\\ &&+\,\frac{1}{2}(\boldsymbol\beta-\boldsymbol\beta_{0})' \frac{\partial^2l(\boldsymbol\beta_0)}{\partial\boldsymbol\beta\partial\boldsymbol\beta'}(\boldsymbol\beta-\boldsymbol\beta_{0})\\ &&+\, o\left(\left\|\hat{\boldsymbol\beta}(\gamma)-\boldsymbol\beta_0\right\|^2\right). \end{array} $$

So by Lemmas 3, 4 and 5, we have

$$ \begin{array}{rll} l(\boldsymbol\beta_{0})-l\left(\hat{\boldsymbol\beta}_c(\gamma)\right) &=& O\left(1/\sqrt{n}+\gamma/n\right)O\left(\sqrt{n\log\log n}\right)\\ &&+\,O(n)O\left(\left(1/\sqrt{n}+\gamma/n\right)^2\right). \end{array} $$

When $\gamma=o(\sqrt{n\log n})$, we have $l(\boldsymbol\beta_{0})-l(\hat{\boldsymbol\beta}_c(\gamma))=o(\log n)$.

In the end, because Lemma 6 says that, when $\gamma>\max\mid(\frac{\partial l}{\partial\boldsymbol\beta})_j\mid=O(\sqrt{n\log\log n})$, it gives a null model with only an intercept, we do not need a tuning parameter γ exceeding $o(\sqrt{n\log n})$. Therefore, $l(\boldsymbol\beta_{0})-l(\hat{\boldsymbol\beta}_c(\gamma))=o(\log n)$ is achievable for all correct models given by $\hat{\boldsymbol\beta}(\gamma)$. Therefore, the BIC γ-selector selects the correct model with smallest number of parameters among all the submodels $\hat{\boldsymbol\beta}(\gamma)$ presents.