Interspike interval correlation in a stochastic exponential integrate-and-fire model with subthreshold and spike-triggered adaptation

Abstract

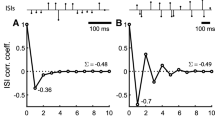
We study the spike statistics of an adaptive exponential integrate-and-fire neuron stimulated by white Gaussian current noise. We derive analytical approximations for the coefficient of variation and the serial correlation coefficient of the interspike interval assuming that the neuron operates in the mean-driven tonic firing regime and that the stochastic input is weak. Our result for the serial correlation coefficient has the form of a geometric sequence and is confirmed by the comparison to numerical simulations. The theory predicts various patterns of interval correlations (positive or negative at lag one, monotonically decreasing or oscillating) depending on the strength of the spike-triggered and subthreshold components of the adaptation current. In particular, for pure subthreshold adaptation we find strong positive ISI correlations that are usually ascribed to positive correlations in the input current. Our results i) provide an alternative explanation for interspike-interval correlations observed in vivo, ii) may be useful in fitting point neuron models to experimental data, and iii) may be instrumental in exploring the role of adaptation currents for signal detection and signal transmission in single neurons.

Appendix

1.1 Phase response curves (PRC)

The phase-dependent sensitivity of the ISI in response to a stimulus $\epsilon \delta (t-t^{\prime })$ added on the right-hand-side of Eq. (1) can be characterized by the infinitesimal PRC defined as

$$Z(t^{\prime})= - \lim_{\epsilon \rightarrow 0} \frac{\delta T(t^{\prime}, \epsilon)}{\epsilon} $$

with $\delta T(t^{\prime }, \epsilon )$ being the change of the spike period due the δ-stimulation at the “phase” $t^{\prime }\in [0,T^{*}]$. Analogously, the sensitivity with respect to a perturbation $\epsilon \tau _{a}\delta (t-t^{\prime })$ added on the right-hand-side of Eq. (2) can be likewise defined by the negative infinitesimal relative change of the ISI. This sensitivity with respect to the adaptation variable will be denoted by $Z_{a}(t^{\prime })$. Let the linearized system (1-2) be $\dot {X}=J(t)X$, and X=(v,a)^T and J(t) being the Jacobian matrix evaluated at the deterministic limit cycle (v ₀(t),a ₀(t))^T, then the infinitesimal PRCs Z(t) and Z _a (t) satisfy the adjoint equations $\dot {Y}=-J^{T}Y$ with Y=(Z,Z _a )^T (Ermentrout and Terman 2010) as

$$ \left(\begin{array}{c} \dot Z \\ \dot Z_{a} \end{array}\right)= \left(\begin{array}{cc}- \frac{\partial f(v_{0},a_{0})}{\partial v} & -\frac{A}{\tau_{a}} \\ 1 & \frac{1}{\tau_{a}} \end{array}\right) \left(\begin{array}{c} Z \\ Z_{a} \end{array}\right) $$

(34)

with the normalization condition $\dot v_{0}(t) Z(t)+ \dot a_{0}(t)Z_{a}(t)=1$, which can be calculated directly. On the threshold, a perturbation does not change the phase implying Z _a (T ^∗)=0 (Schwalger and Lindner 2013). With this condition, the second equation of Eq. (34) satisfying $\dot Z_{a} = Z+ \frac {1}{\tau _{a}} Z_{a}$ leads to $Z_{a}(0)=-{\int }_{0}^{T^{*}} Z(s)e^{\frac {-s}{\tau _{a}}}ds.$

1.2 Green’s function

To calculate $\frac {A}{\tau _{a}}{\int }_{0}^{T^{*}}dt^{\prime }\delta v(t^{\prime })e^{\frac {-(T^{*}-t^{\prime })}{\tau _{a}}}$, we start with the perturbation dynamics

$$\begin{array}{@{}rcl@{}} \delta \dot v & = & \lambda(t) \delta v -\delta a +\xi(t), \end{array} $$

(35)

$$\begin{array}{@{}rcl@{}} \tau_{a} \delta \dot a & = & -\delta a +A \delta v, \end{array} $$

(36)

where λ(t)=d f(v ₀(t))/d v, with initial conditions $\delta v(0)=0, \delta a(0)=\delta a_{i}$. The solution to Eq. (36) is $\delta a(t)= \delta a_{i} e^{-t/{\tau _{a}}} + \delta x(t)$, where δ x(t) satisfies $\tau _{a} \delta \dot x = -\delta x +A \delta v$ with δ x(0)=0. Hence, the desired quantity is given by

$$\begin{array}{@{}rcl@{}} &&\frac{A}{\tau_{a}} {\int}_{0}^{T^{*}} \delta v(t^{\prime})e^{-(T^{*}-t^{\prime})/{\tau_{a}}}\, dt^{\prime}=\delta x(T^{*})\\ &&=A{\int}_{0}^{T^{*}}\mathrm{d}t^{\prime}\,\delta X_{g}(T^{*},t^{\prime})[\xi(t^{\prime})-\delta a_{i}e^{-t^{\prime}/\tau_{a}}]. \end{array} $$

(37)

Here, we used the Green’s function $\delta X_{g}(t,t^{\prime })$ which is the solution of

$$\begin{array}{@{}rcl@{}} \frac{\partial}{\partial t}\delta v_{g}(t,t^{\prime}) & \!\,=\, & \lambda(t) \delta v_{g}(t,t^{\prime}) \,-\,A\delta X_{g}(t,t^{\prime}) \,+\,\delta (t\,-\,t^{\prime}), \end{array} $$

(38)

$$\begin{array}{@{}rcl@{}} \tau_{a} \frac{\partial}{\partial t}\delta X_{g}(t,t^{\prime}) & \!\,=\, & \!-\delta X_{g}(t,t^{\prime}) +\delta v_{g}(t,t^{\prime}), \end{array} $$

(39)

with $\delta v_{g}(0, t^{\prime })=\delta X_{g}(0,t^{\prime })=0$ and $t^{\prime }\in [0,T^{*}]$. The two-dimensional system for the Greens function is solved numerically.